Question Number 52670 by maxmathsup by imad last updated on 11/Jan/19
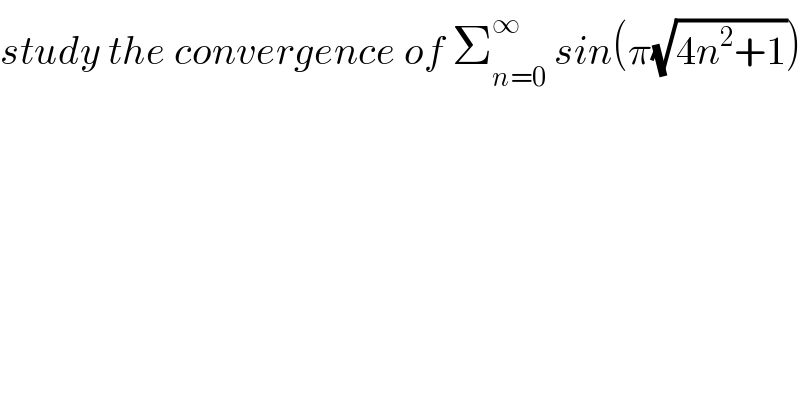
$${study}\:{the}\:{convergence}\:{of}\:\sum_{{n}=\mathrm{0}} ^{\infty} \:{sin}\left(\pi\sqrt{\mathrm{4}{n}^{\mathrm{2}} +\mathrm{1}}\right) \\ $$
Commented by maxmathsup by imad last updated on 12/Jan/19
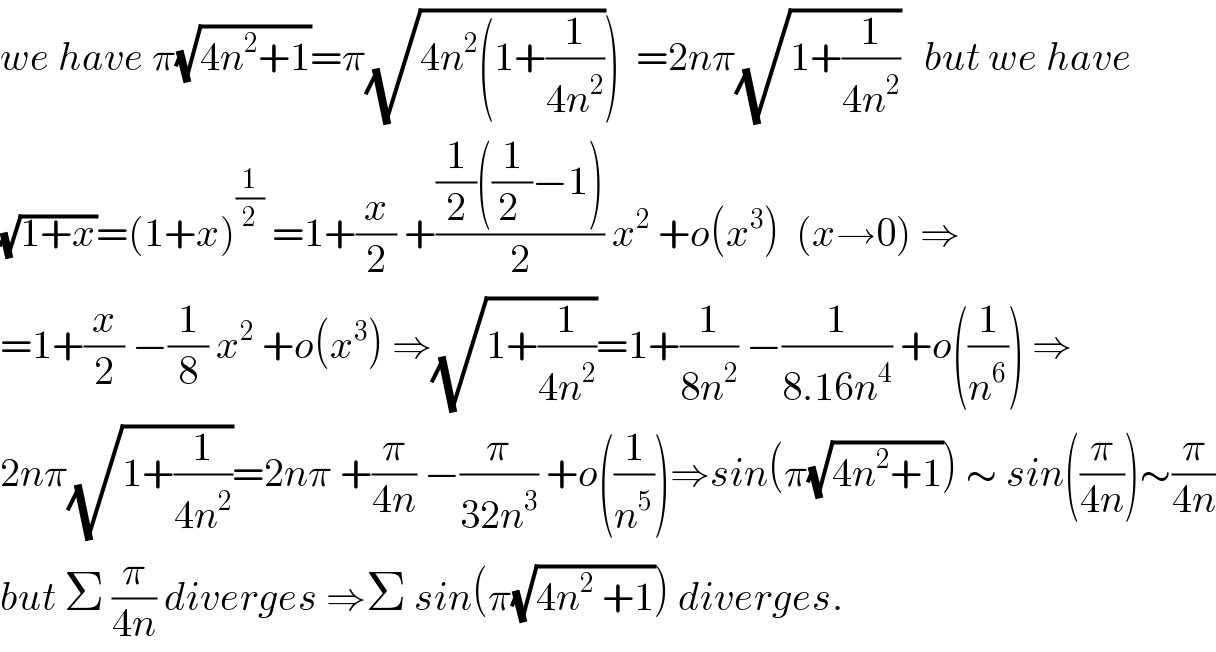
$$\left.{we}\:{have}\:\pi\sqrt{\mathrm{4}{n}^{\mathrm{2}} +\mathrm{1}}=\pi\sqrt{\mathrm{4}{n}^{\mathrm{2}} \left(\mathrm{1}+\frac{\mathrm{1}}{\mathrm{4}{n}^{\mathrm{2}} }\right.}\right)\:\:=\mathrm{2}{n}\pi\sqrt{\mathrm{1}+\frac{\mathrm{1}}{\mathrm{4}{n}^{\mathrm{2}} }}\:\:\:{but}\:{we}\:{have} \\ $$$$\sqrt{\mathrm{1}+{x}}=\left(\mathrm{1}+{x}\right)^{\frac{\mathrm{1}}{\mathrm{2}}} \:=\mathrm{1}+\frac{{x}}{\mathrm{2}}\:+\frac{\frac{\mathrm{1}}{\mathrm{2}}\left(\frac{\mathrm{1}}{\mathrm{2}\:}−\mathrm{1}\right)}{\mathrm{2}}\:{x}^{\mathrm{2}} \:+{o}\left({x}^{\mathrm{3}} \right)\:\:\left({x}\rightarrow\mathrm{0}\right)\:\Rightarrow \\ $$$$=\mathrm{1}+\frac{{x}}{\mathrm{2}}\:−\frac{\mathrm{1}}{\mathrm{8}}\:{x}^{\mathrm{2}} \:+{o}\left({x}^{\mathrm{3}} \right)\:\Rightarrow\sqrt{\mathrm{1}+\frac{\mathrm{1}}{\mathrm{4}{n}^{\mathrm{2}} }}=\mathrm{1}+\frac{\mathrm{1}}{\mathrm{8}{n}^{\mathrm{2}} }\:−\frac{\mathrm{1}}{\mathrm{8}.\mathrm{16}{n}^{\mathrm{4}} }\:+{o}\left(\frac{\mathrm{1}}{{n}^{\mathrm{6}} }\right)\:\Rightarrow \\ $$$$\mathrm{2}{n}\pi\sqrt{\mathrm{1}+\frac{\mathrm{1}}{\mathrm{4}{n}^{\mathrm{2}} }}=\mathrm{2}{n}\pi\:+\frac{\pi}{\mathrm{4}{n}}\:−\frac{\pi}{\mathrm{32}{n}^{\mathrm{3}} }\:+{o}\left(\frac{\mathrm{1}}{{n}^{\mathrm{5}} }\right)\Rightarrow{sin}\left(\pi\sqrt{\mathrm{4}{n}^{\mathrm{2}} +\mathrm{1}}\right)\:\sim\:{sin}\left(\frac{\pi}{\mathrm{4}{n}}\right)\sim\frac{\pi}{\mathrm{4}{n}} \\ $$$${but}\:\Sigma\:\frac{\pi}{\mathrm{4}{n}}\:{diverges}\:\Rightarrow\Sigma\:{sin}\left(\pi\sqrt{\mathrm{4}{n}^{\mathrm{2}} \:+\mathrm{1}}\right)\:{diverges}. \\ $$
Answered by tanmay.chaudhury50@gmail.com last updated on 11/Jan/19

$$\frac{\mathrm{4}{n}^{\mathrm{2}} +\mathrm{1}}{\mathrm{2}}\geqslant\sqrt{\mathrm{4}{n}^{\mathrm{2}} ×\mathrm{1}}\: \\ $$$$\mathrm{4}{n}^{\mathrm{2}} +\mathrm{1}\geqslant\mathrm{4}{n} \\ $$$$\sqrt{\mathrm{4}{n}^{\mathrm{2}} +\mathrm{1}}\:\geqslant\sqrt{\mathrm{4}{n}}\: \\ $$$${sin}\left(\pi\sqrt{\mathrm{4}{n}^{\mathrm{2}} +\mathrm{1}}\:\right)\approx{sin}\left(\pi×\mathrm{2}\sqrt{{n}}\:\right) \\ $$$${sin}\left(\sqrt{{n}}\:×\mathrm{2}\pi\right) \\ $$$$\left.\mathrm{1}\right){now}\:{when}\:{n}\:{is}\:{perfect}\:{square} \\ $$$${sin}\left(\sqrt{{n}}\:×\mathrm{2}\pi\right)=\mathrm{0} \\ $$$$\left.\mathrm{2}\right)\sqrt{{n}}\:={I}+{f}\:{I}={integer} \\ $$$${f}={fractional}\:{part} \\ $$$$ \\ $$$${sin}\left\{\left({I}+{f}\right)\mathrm{2}\pi\right\} \\ $$$$={sin}\left\{{I}×\mathrm{2}\pi+{f}×\mathrm{2}\pi\right\} \\ $$$$={sin}\left({f}×\mathrm{2}\pi\right) \\ $$$$\:\mathrm{1}\geqslant{sin}\left(\mathrm{2}\pi{f}\right)\geqslant−\mathrm{1} \\ $$$${so}\:\underset{{n}=\mathrm{0}} {\overset{\infty} {\sum}}{sin}\left(\pi\sqrt{\mathrm{4}{n}^{\mathrm{2}} +\mathrm{1}}\:\right)\:{does}\:{not}\:{converge} \\ $$$$\:\:\:\:\underset{{n}=\mathrm{0}} {\overset{\infty} {\sum}}{sin}\left(\pi\sqrt{\mathrm{4}{n}^{\mathrm{2}} +\mathrm{1}}\:\right)\:{oscilates}\:{between}\:\pm\:\infty \\ $$$${i}\:{have}\:{tried}\:{to}\:{solve}\:…{pls}\:{check}\:{is}\:{the}\:{logic} \\ $$$${true}… \\ $$
