Question Number 118395 by TANMAY PANACEA last updated on 17/Oct/20
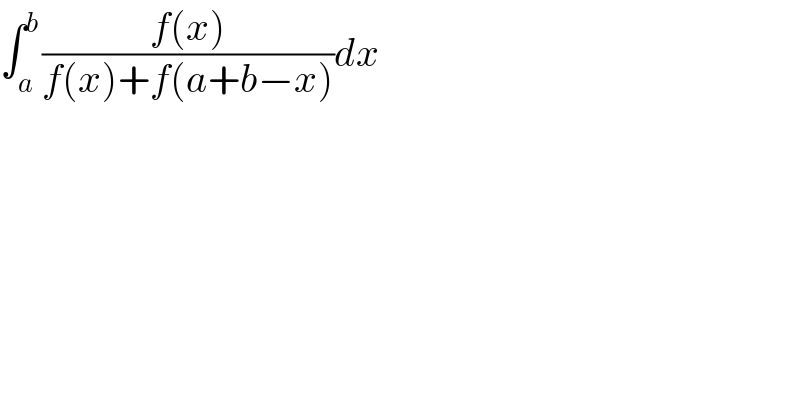
$$\int_{{a}} ^{{b}} \frac{{f}\left({x}\right)}{{f}\left({x}\right)+{f}\left({a}+{b}−{x}\right)}{dx} \\ $$
Commented by Dwaipayan Shikari last updated on 17/Oct/20

$$\frac{{b}−{a}}{\mathrm{2}} \\ $$
Commented by TANMAY PANACEA last updated on 17/Oct/20

$${thank}\:{you}…{durga}\:{pujo}\:{hochhe} \\ $$
Commented by Dwaipayan Shikari last updated on 17/Oct/20

$${From}\:\mathrm{23}\:{oct} \\ $$
Commented by Dwaipayan Shikari last updated on 17/Oct/20
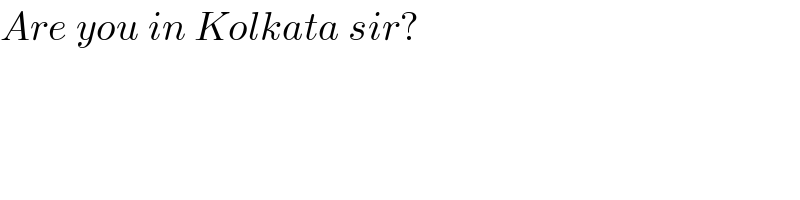
$${Are}\:{you}\:{in}\:{Kolkata}\:{sir}? \\ $$
Commented by TANMAY PANACEA last updated on 17/Oct/20
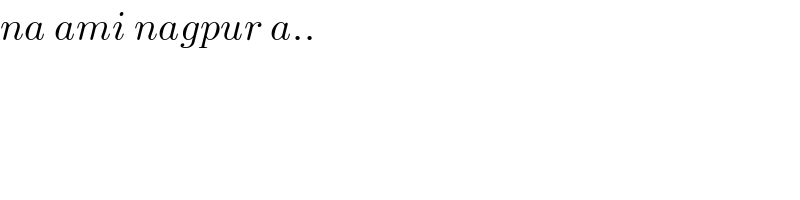
$${na}\:{ami}\:{nagpur}\:{a}..\: \\ $$
Answered by mathmax by abdo last updated on 17/Oct/20
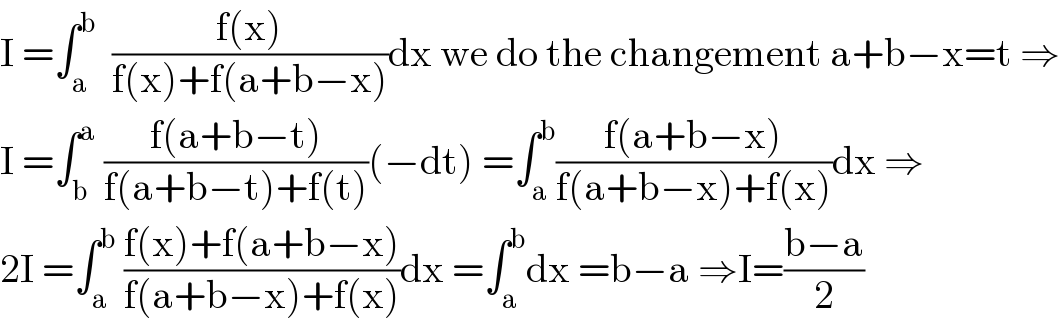
$$\mathrm{I}\:=\int_{\mathrm{a}} ^{\mathrm{b}} \:\:\frac{\mathrm{f}\left(\mathrm{x}\right)}{\mathrm{f}\left(\mathrm{x}\right)+\mathrm{f}\left(\mathrm{a}+\mathrm{b}−\mathrm{x}\right)}\mathrm{dx}\:\mathrm{we}\:\mathrm{do}\:\mathrm{the}\:\mathrm{changement}\:\mathrm{a}+\mathrm{b}−\mathrm{x}=\mathrm{t}\:\Rightarrow \\ $$$$\mathrm{I}\:=\int_{\mathrm{b}} ^{\mathrm{a}} \:\frac{\mathrm{f}\left(\mathrm{a}+\mathrm{b}−\mathrm{t}\right)}{\mathrm{f}\left(\mathrm{a}+\mathrm{b}−\mathrm{t}\right)+\mathrm{f}\left(\mathrm{t}\right)}\left(−\mathrm{dt}\right)\:=\int_{\mathrm{a}} ^{\mathrm{b}} \frac{\mathrm{f}\left(\mathrm{a}+\mathrm{b}−\mathrm{x}\right)}{\mathrm{f}\left(\mathrm{a}+\mathrm{b}−\mathrm{x}\right)+\mathrm{f}\left(\mathrm{x}\right)}\mathrm{dx}\:\Rightarrow \\ $$$$\mathrm{2I}\:=\int_{\mathrm{a}} ^{\mathrm{b}} \:\frac{\mathrm{f}\left(\mathrm{x}\right)+\mathrm{f}\left(\mathrm{a}+\mathrm{b}−\mathrm{x}\right)}{\mathrm{f}\left(\mathrm{a}+\mathrm{b}−\mathrm{x}\right)+\mathrm{f}\left(\mathrm{x}\right)}\mathrm{dx}\:=\int_{\mathrm{a}} ^{\mathrm{b}} \mathrm{dx}\:=\mathrm{b}−\mathrm{a}\:\Rightarrow\mathrm{I}=\frac{\mathrm{b}−\mathrm{a}}{\mathrm{2}} \\ $$
Commented by TANMAY PANACEA last updated on 17/Oct/20

$${thank}\:{you}\:{sir} \\ $$
Commented by Bird last updated on 17/Oct/20
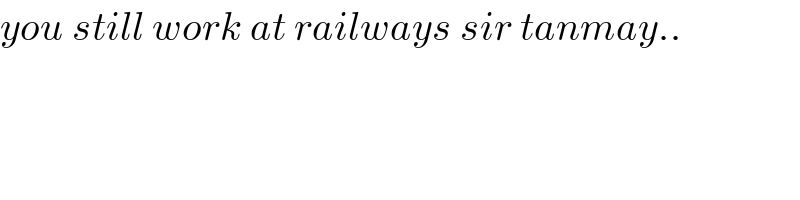
$${you}\:{still}\:{work}\:{at}\:{railways}\:{sir}\:{tanmay}.. \\ $$
Commented by TANMAY PANACEA last updated on 17/Oct/20
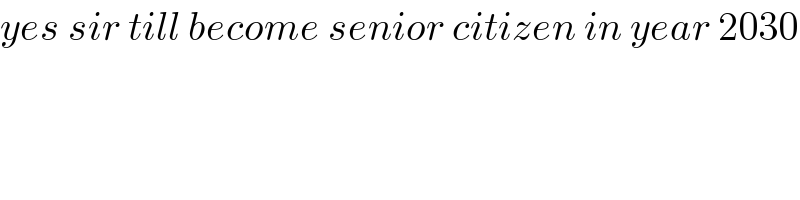
$${yes}\:{sir}\:{till}\:{become}\:{senior}\:{citizen}\:{in}\:{year}\:\mathrm{2030} \\ $$
Commented by mathmax by abdo last updated on 17/Oct/20
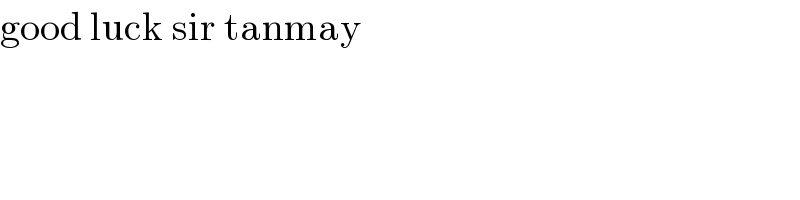
$$\mathrm{good}\:\mathrm{luck}\:\mathrm{sir}\:\mathrm{tanmay} \\ $$
Answered by TANMAY PANACEA last updated on 17/Oct/20

$${formula} \\ $$$$\int_{{q}} ^{{p}} {f}\left({x}\right){dx}=\int_{{q}} ^{{p}} {f}\left({p}+{q}−{x}\right){dx} \\ $$$${I}=\int_{{a}} ^{{b}} \frac{{f}\left({x}\right)}{{f}\left({x}\right)+{f}\left({a}+{b}−{x}\right)}{dx} \\ $$$$=\int_{{a}} ^{{b}} \frac{{f}\left({a}+{b}−{x}\right)}{{f}\left({a}+{b}−{x}\right)+{f}\left\{\left({a}+{b}−\left({a}+{b}−{x}\right)\right\}\right.}{dx} \\ $$$$=\int_{{a}} ^{{b}} \frac{{f}\left({a}+{b}−{x}\right)}{{f}\left({a}+{b}−{x}\right)+{f}\left({x}\right)}{dx} \\ $$$$\mathrm{2}{I}=\int_{{a}} ^{{b}} {dx} \\ $$$${I}=\frac{{b}−{a}}{\mathrm{2}} \\ $$$$ \\ $$
Commented by bramlexs22 last updated on 17/Oct/20

$${this}\:{is}\:{formula}\:{King}\:{Integral}\:{sir}? \\ $$
