Question Number 53034 by gopikrishnan005@gmail.com last updated on 16/Jan/19
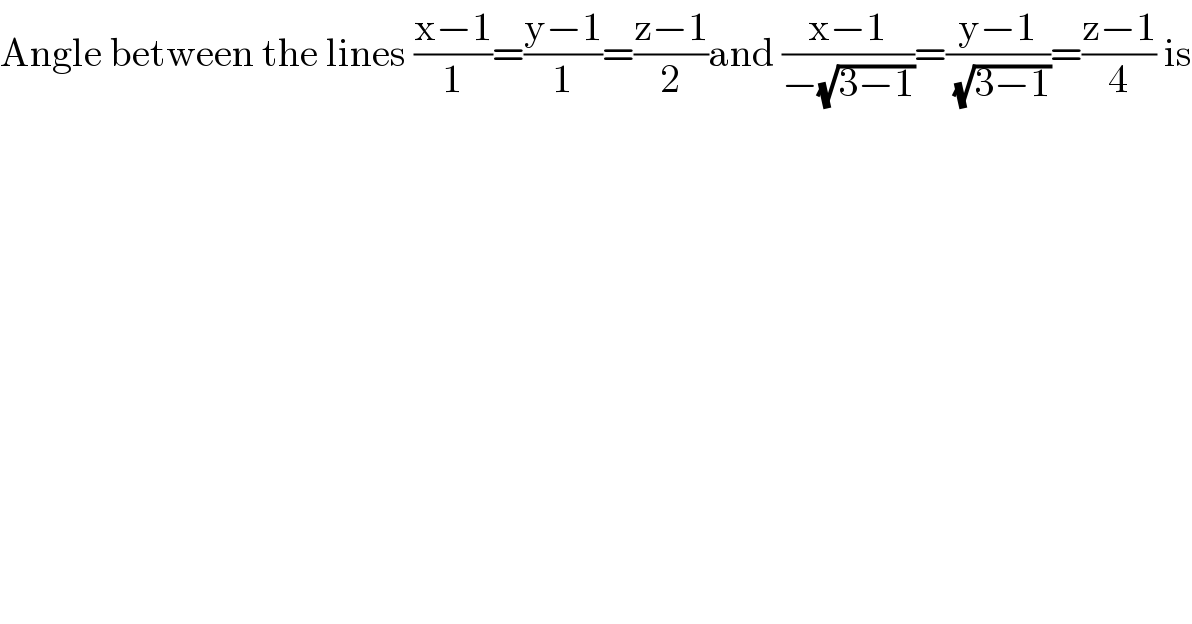
$$\mathrm{Angle}\:\mathrm{between}\:\mathrm{the}\:\mathrm{lines}\:\frac{\mathrm{x}−\mathrm{1}}{\mathrm{1}}=\frac{\mathrm{y}−\mathrm{1}}{\mathrm{1}}=\frac{\mathrm{z}−\mathrm{1}}{\mathrm{2}}\mathrm{and}\:\frac{\mathrm{x}−\mathrm{1}}{−\sqrt{\mathrm{3}−\mathrm{1}}}=\frac{\mathrm{y}−\mathrm{1}}{\:\sqrt{\mathrm{3}−\mathrm{1}}}=\frac{\mathrm{z}−\mathrm{1}}{\mathrm{4}}\:\mathrm{is} \\ $$
Answered by tanmay.chaudhury50@gmail.com last updated on 16/Jan/19
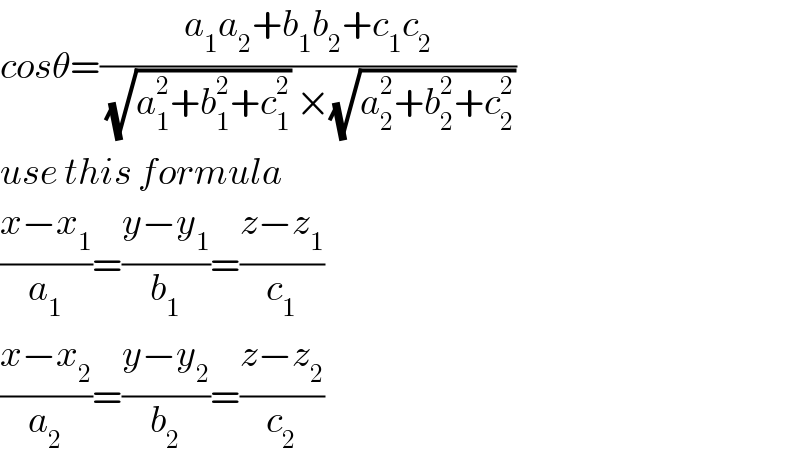
$${cos}\theta=\frac{{a}_{\mathrm{1}} {a}_{\mathrm{2}} +{b}_{\mathrm{1}} {b}_{\mathrm{2}} +{c}_{\mathrm{1}} {c}_{\mathrm{2}} }{\:\sqrt{{a}_{\mathrm{1}} ^{\mathrm{2}} +{b}_{\mathrm{1}} ^{\mathrm{2}} +{c}_{\mathrm{1}} ^{\mathrm{2}} }\:×\sqrt{{a}_{\mathrm{2}} ^{\mathrm{2}} +{b}_{\mathrm{2}} ^{\mathrm{2}} +{c}_{\mathrm{2}} ^{\mathrm{2}} }} \\ $$$${use}\:{this}\:{formula} \\ $$$$\frac{{x}−{x}_{\mathrm{1}} }{{a}_{\mathrm{1}} }=\frac{{y}−{y}_{\mathrm{1}} }{{b}_{\mathrm{1}} }=\frac{{z}−{z}_{\mathrm{1}} }{{c}_{\mathrm{1}} } \\ $$$$\frac{{x}−{x}_{\mathrm{2}} }{{a}_{\mathrm{2}} }=\frac{{y}−{y}_{\mathrm{2}} }{{b}_{\mathrm{2}} }=\frac{{z}−{z}_{\mathrm{2}} }{{c}_{\mathrm{2}} }\:\:\: \\ $$
Answered by ajfour last updated on 16/Jan/19
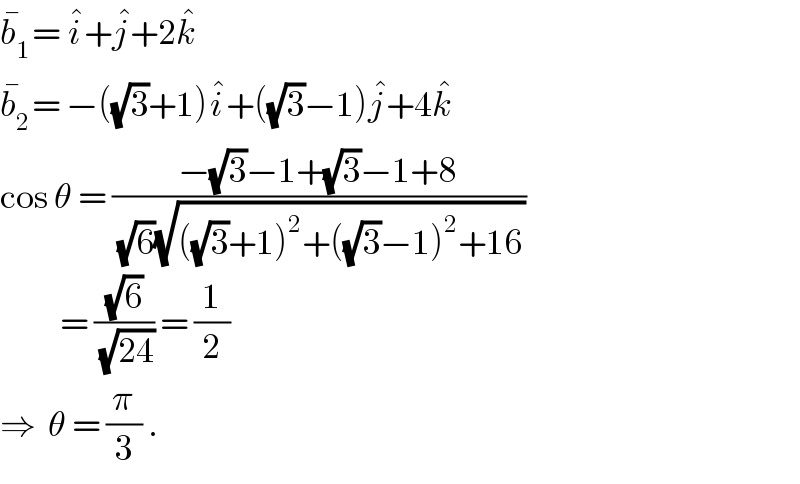
$$\bar {{b}}_{\mathrm{1}} =\:\hat {{i}}+\hat {{j}}+\mathrm{2}\hat {{k}} \\ $$$$\bar {{b}}_{\mathrm{2}} =\:−\left(\sqrt{\mathrm{3}}+\mathrm{1}\right)\hat {{i}}+\left(\sqrt{\mathrm{3}}−\mathrm{1}\right)\hat {{j}}+\mathrm{4}\hat {{k}} \\ $$$$\mathrm{cos}\:\theta\:=\:\frac{−\sqrt{\mathrm{3}}−\mathrm{1}+\sqrt{\mathrm{3}}−\mathrm{1}+\mathrm{8}}{\:\sqrt{\mathrm{6}}\sqrt{\left(\sqrt{\mathrm{3}}+\mathrm{1}\right)^{\mathrm{2}} +\left(\sqrt{\mathrm{3}}−\mathrm{1}\right)^{\mathrm{2}} +\mathrm{16}}} \\ $$$$\:\:\:\:\:\:\:\:\:\:=\:\frac{\sqrt{\mathrm{6}}}{\:\sqrt{\mathrm{24}}}\:=\:\frac{\mathrm{1}}{\mathrm{2}}\: \\ $$$$\Rightarrow\:\:\theta\:=\:\frac{\pi}{\mathrm{3}}\:. \\ $$
