Menu Close

Given-f-x-f-x-pi-6-x-R-if-0-pi-6-f-x-dx-T-find-the-value-of-pi-4pi-3-f-x-pi-dx-nice-integral-

Tinku Tara
Pin




Question Number 131496 by benjo_mathlover last updated on 05/Feb/21
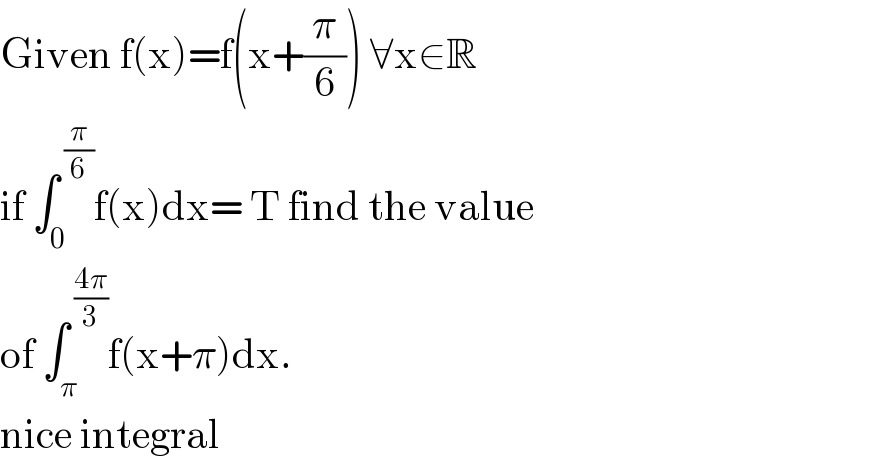
Given f(x)=f(x+(π/6)) ∀x∈R if ∫_0 ^( (π/6)) f(x)dx= T find the value of ∫_π ^( ((4π)/3)) f(x+π)dx. nice integral
$$\mathrm{Given}\:\mathrm{f}\left(\mathrm{x}\right)=\mathrm{f}\left(\mathrm{x}+\frac{\pi}{\mathrm{6}}\right)\:\forall\mathrm{x}\in\mathbb{R} \\ $$$$\mathrm{if}\:\int_{\mathrm{0}} ^{\:\frac{\pi}{\mathrm{6}}} \mathrm{f}\left(\mathrm{x}\right)\mathrm{dx}=\:\mathrm{T}\:\mathrm{find}\:\mathrm{the}\:\mathrm{value} \\ $$$$\mathrm{of}\:\int_{\pi} ^{\:\frac{\mathrm{4}\pi}{\mathrm{3}}} \mathrm{f}\left(\mathrm{x}+\pi\right)\mathrm{dx}. \\ $$$$\mathrm{nice}\:\mathrm{integral} \\ $$
Answered by talminator2856791 last updated on 05/Feb/21
2T
$$\:\mathrm{2T} \\ $$
Commented by benjo_mathlover last updated on 05/Feb/21
why?
$$\mathrm{why}? \\ $$
Answered by EDWIN88 last updated on 05/Feb/21
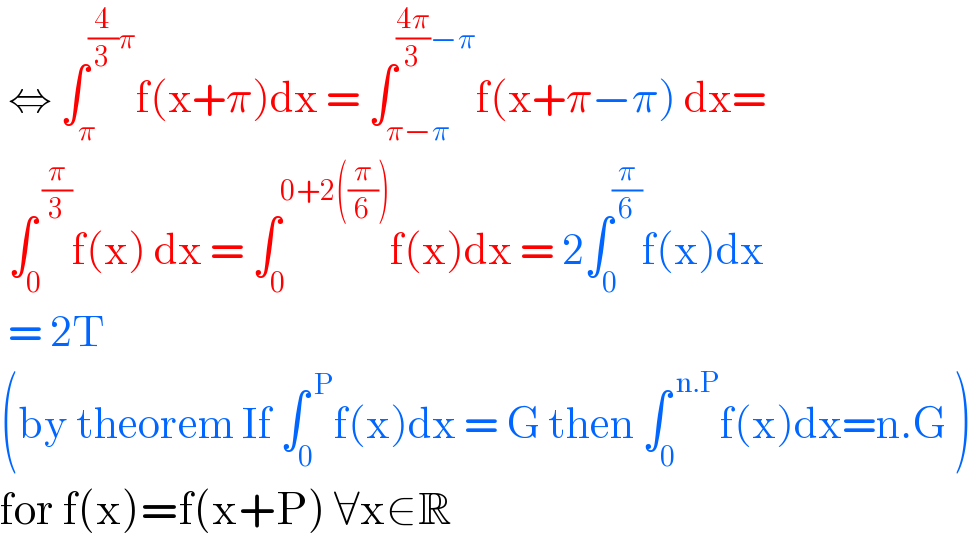
⇔ ∫_π ^((4/3)π) f(x+π)dx = ∫_(π−π) ^(((4π)/3)−π) f(x+π−π) dx= ∫_0 ^( (π/3)) f(x) dx = ∫_0 ^(0+2((π/6))) f(x)dx = 2∫_0 ^(π/6) f(x)dx = 2T (by theorem If ∫_0 ^( P) f(x)dx = G then ∫_0 ^( n.P) f(x)dx=n.G ) for f(x)=f(x+P) ∀x∈R
$$\:\Leftrightarrow\:\int_{\pi} ^{\frac{\mathrm{4}}{\mathrm{3}}\pi} \mathrm{f}\left(\mathrm{x}+\pi\right)\mathrm{dx}\:=\:\int_{\pi−\pi} ^{\frac{\mathrm{4}\pi}{\mathrm{3}}−\pi} \mathrm{f}\left(\mathrm{x}+\pi−\pi\right)\:\mathrm{dx}= \\ $$$$\:\int_{\mathrm{0}} ^{\:\frac{\pi}{\mathrm{3}}} \mathrm{f}\left(\mathrm{x}\right)\:\mathrm{dx}\:=\:\int_{\mathrm{0}} ^{\mathrm{0}+\mathrm{2}\left(\frac{\pi}{\mathrm{6}}\right)} \mathrm{f}\left(\mathrm{x}\right)\mathrm{dx}\:=\:\mathrm{2}\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{6}}} \mathrm{f}\left(\mathrm{x}\right)\mathrm{dx} \\ $$$$\:=\:\mathrm{2T}\: \\ $$$$\left(\mathrm{by}\:\mathrm{theorem}\:\mathrm{If}\:\int_{\mathrm{0}} ^{\:\mathrm{P}} \mathrm{f}\left(\mathrm{x}\right)\mathrm{dx}\:=\:\mathrm{G}\:\mathrm{then}\:\int_{\mathrm{0}} ^{\:\mathrm{n}.\mathrm{P}} \mathrm{f}\left(\mathrm{x}\right)\mathrm{dx}=\mathrm{n}.\mathrm{G}\:\right) \\ $$$$\mathrm{for}\:\mathrm{f}\left(\mathrm{x}\right)=\mathrm{f}\left(\mathrm{x}+\mathrm{P}\right)\:\forall\mathrm{x}\in\mathbb{R} \\ $$
Commented by benjo_mathlover last updated on 05/Feb/21
thank you
$$\mathrm{thank}\:\mathrm{you} \\ $$
Answered by mr W last updated on 05/Feb/21
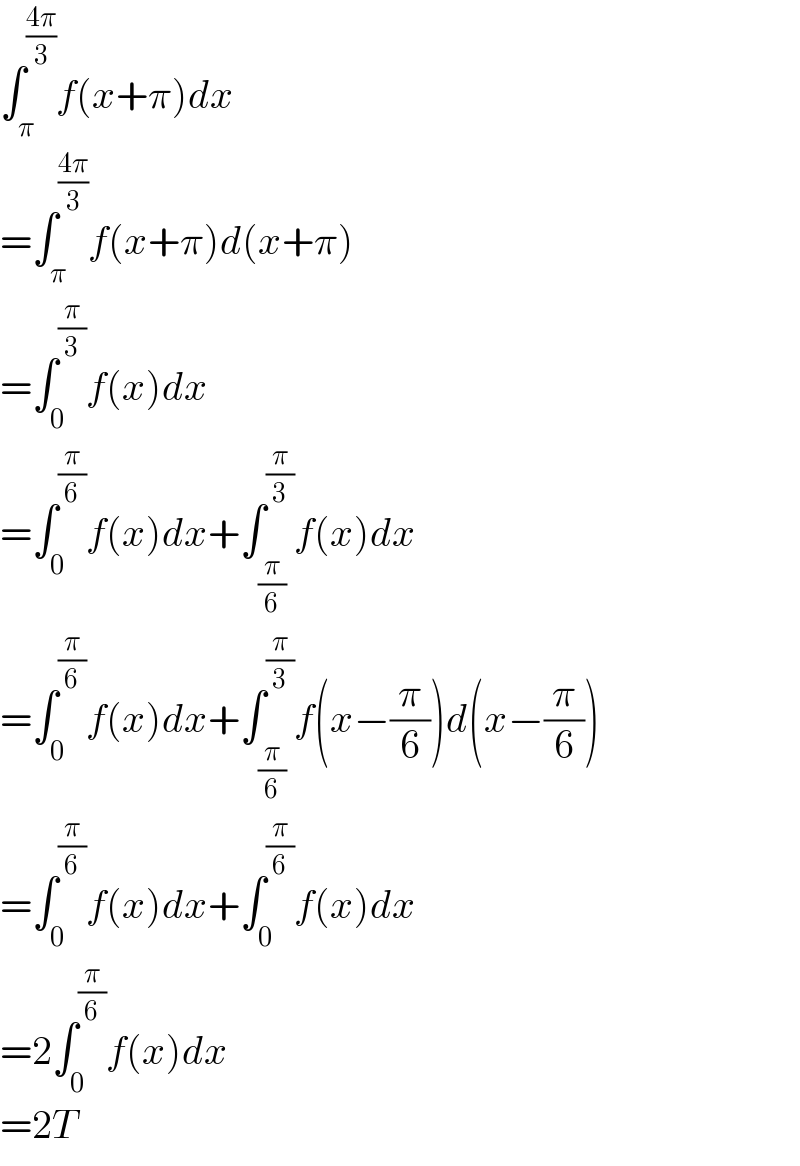
∫_π ^((4π)/3) f(x+π)dx =∫_π ^((4π)/3) f(x+π)d(x+π) =∫_0 ^(π/3) f(x)dx =∫_0 ^(π/6) f(x)dx+∫_(π/6) ^(π/3) f(x)dx =∫_0 ^(π/6) f(x)dx+∫_(π/6) ^(π/3) f(x−(π/6))d(x−(π/6)) =∫_0 ^(π/6) f(x)dx+∫_0 ^(π/6) f(x)dx =2∫_0 ^(π/6) f(x)dx =2T
$$\int_{\pi} ^{\frac{\mathrm{4}\pi}{\mathrm{3}}} {f}\left({x}+\pi\right){dx} \\ $$$$=\int_{\pi} ^{\frac{\mathrm{4}\pi}{\mathrm{3}}} {f}\left({x}+\pi\right){d}\left({x}+\pi\right) \\ $$$$=\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{3}}} {f}\left({x}\right){dx} \\ $$$$=\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{6}}} {f}\left({x}\right){dx}+\int_{\frac{\pi}{\mathrm{6}}} ^{\frac{\pi}{\mathrm{3}}} {f}\left({x}\right){dx} \\ $$$$=\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{6}}} {f}\left({x}\right){dx}+\int_{\frac{\pi}{\mathrm{6}}} ^{\frac{\pi}{\mathrm{3}}} {f}\left({x}−\frac{\pi}{\mathrm{6}}\right){d}\left({x}−\frac{\pi}{\mathrm{6}}\right) \\ $$$$=\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{6}}} {f}\left({x}\right){dx}+\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{6}}} {f}\left({x}\right){dx} \\ $$$$=\mathrm{2}\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{6}}} {f}\left({x}\right){dx} \\ $$$$=\mathrm{2}{T} \\ $$
Commented by benjo_mathlover last updated on 05/Feb/21
thank you
$$\mathrm{thank}\:\mathrm{you} \\ $$

Pin