Menu Close

x-sin-x-1-cos-2-x-dx-

Tinku Tara 0 Comments
Pin




Question Number 118668 by bemath last updated on 19/Oct/20
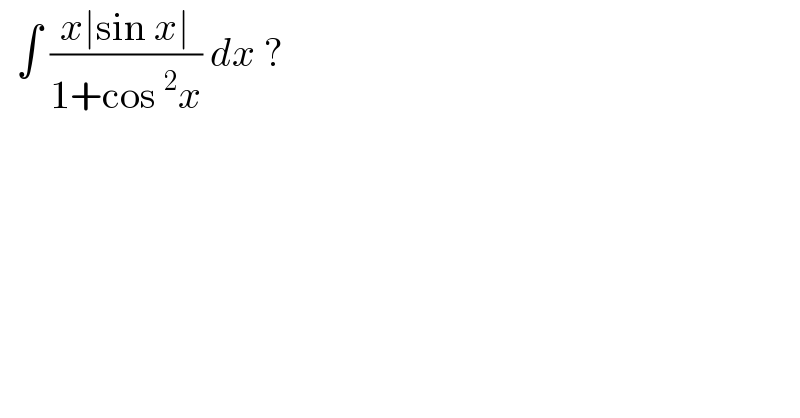
∫ ((x∣sin x∣)/(1+cos^2 x)) dx ?
$$\:\:\int\:\frac{{x}\mid\mathrm{sin}\:{x}\mid}{\mathrm{1}+\mathrm{cos}\:^{\mathrm{2}} {x}}\:{dx}\:? \\ $$
Answered by Lordose last updated on 19/Oct/20
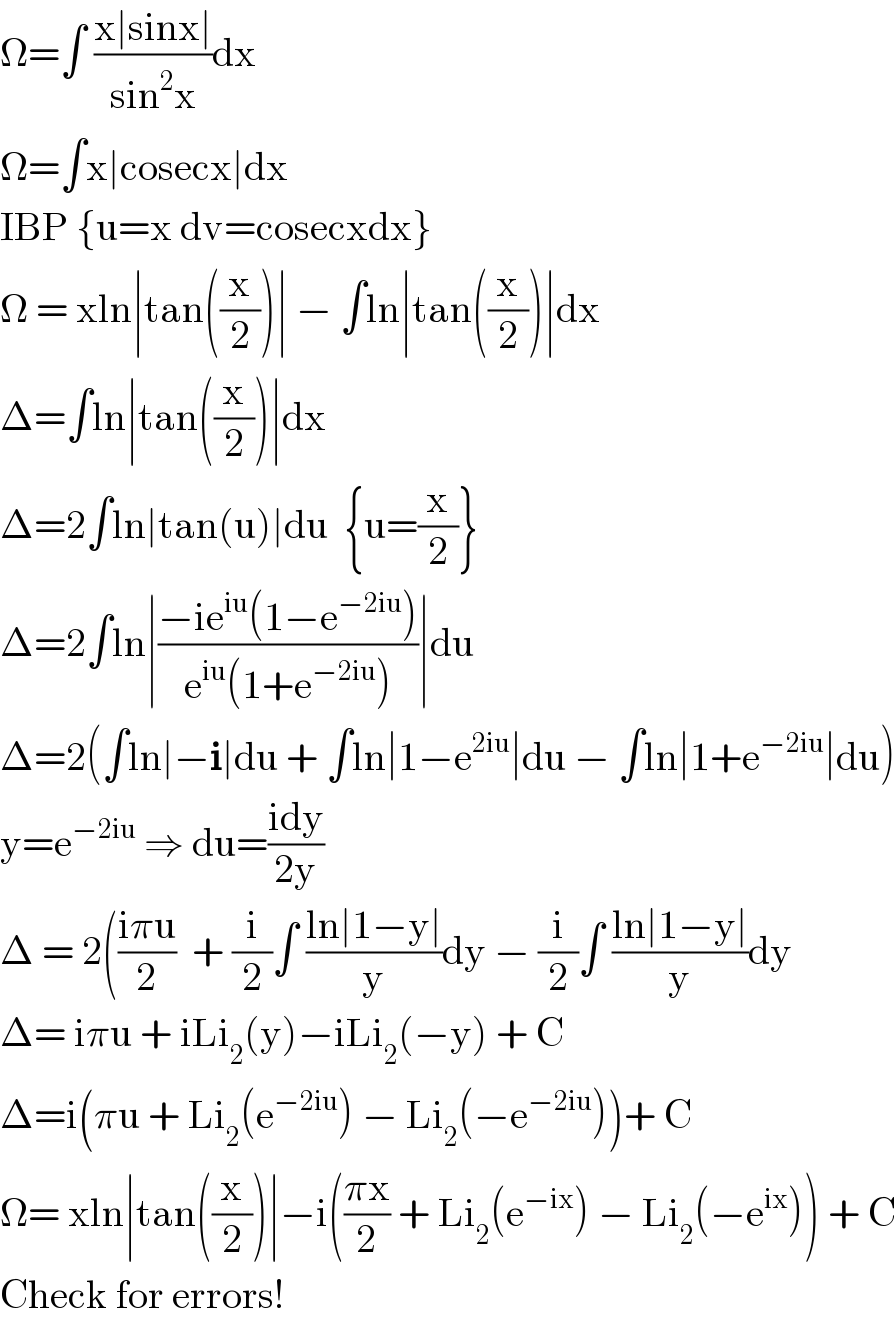
Ω=∫ ((x∣sinx∣)/(sin^2 x))dx Ω=∫x∣cosecx∣dx IBP {u=x dv=cosecxdx} Ω = xln∣tan((x/2))∣ − ∫ln∣tan((x/2))∣dx Δ=∫ln∣tan((x/2))∣dx Δ=2∫ln∣tan(u)∣du {u=(x/2)} Δ=2∫ln∣((−ie^(iu) (1−e^(−2iu) ))/(e^(iu) (1+e^(−2iu) )))∣du Δ=2(∫ln∣−i∣du + ∫ln∣1−e^(2iu) ∣du − ∫ln∣1+e^(−2iu) ∣du) y=e^(−2iu) ⇒ du=((idy)/(2y)) Δ = 2(((iπu)/2) + (i/2)∫ ((ln∣1−y∣)/y)dy − (i/2)∫ ((ln∣1−y∣)/y)dy Δ= iπu + iLi_2 (y)−iLi_2 (−y) + C Δ=i(πu + Li_2 (e^(−2iu) ) − Li_2 (−e^(−2iu) ))+ C Ω= xln∣tan((x/2))∣−i(((πx)/2) + Li_2 (e^(−ix) ) − Li_2 (−e^(ix) )) + C Check for errors!
$$\Omega=\int\:\frac{\mathrm{x}\mid\mathrm{sinx}\mid}{\mathrm{sin}^{\mathrm{2}} \mathrm{x}}\mathrm{dx} \\ $$$$\Omega=\int\mathrm{x}\mid\mathrm{cosecx}\mid\mathrm{dx}\: \\ $$$$\mathrm{IBP}\:\left\{\mathrm{u}=\mathrm{x}\:\mathrm{dv}=\mathrm{cosecxdx}\right\} \\ $$$$\Omega\:=\:\mathrm{xln}\mid\mathrm{tan}\left(\frac{\mathrm{x}}{\mathrm{2}}\right)\mid\:−\:\int\mathrm{ln}\mid\mathrm{tan}\left(\frac{\mathrm{x}}{\mathrm{2}}\right)\mid\mathrm{dx} \\ $$$$\Delta=\int\mathrm{ln}\mid\mathrm{tan}\left(\frac{\mathrm{x}}{\mathrm{2}}\right)\mid\mathrm{dx} \\ $$$$\Delta=\mathrm{2}\int\mathrm{ln}\mid\mathrm{tan}\left(\mathrm{u}\right)\mid\mathrm{du}\:\:\left\{\mathrm{u}=\frac{\mathrm{x}}{\mathrm{2}}\right\} \\ $$$$\Delta=\mathrm{2}\int\mathrm{ln}\mid\frac{−\mathrm{ie}^{\mathrm{iu}} \left(\mathrm{1}−\mathrm{e}^{−\mathrm{2iu}} \right)}{\mathrm{e}^{\mathrm{iu}} \left(\mathrm{1}+\mathrm{e}^{−\mathrm{2iu}} \right)}\mid\mathrm{du} \\ $$$$\Delta=\mathrm{2}\left(\int\mathrm{ln}\mid−\boldsymbol{\mathrm{i}}\mid\mathrm{du}\:+\:\int\mathrm{ln}\mid\mathrm{1}−\mathrm{e}^{\mathrm{2iu}} \mid\mathrm{du}\:−\:\int\mathrm{ln}\mid\mathrm{1}+\mathrm{e}^{−\mathrm{2iu}} \mid\mathrm{du}\right) \\ $$$$\mathrm{y}=\mathrm{e}^{−\mathrm{2iu}} \:\Rightarrow\:\mathrm{du}=\frac{\mathrm{idy}}{\mathrm{2y}} \\ $$$$\Delta\:=\:\mathrm{2}\left(\frac{\mathrm{i}\pi\mathrm{u}}{\mathrm{2}}\:\:+\:\frac{\mathrm{i}}{\mathrm{2}}\int\:\frac{\mathrm{ln}\mid\mathrm{1}−\mathrm{y}\mid}{\mathrm{y}}\mathrm{dy}\:−\:\frac{\mathrm{i}}{\mathrm{2}}\int\:\frac{\mathrm{ln}\mid\mathrm{1}−\mathrm{y}\mid}{\mathrm{y}}\mathrm{dy}\right. \\ $$$$\Delta=\:\mathrm{i}\pi\mathrm{u}\:+\:\mathrm{iLi}_{\mathrm{2}} \left(\mathrm{y}\right)−\mathrm{iLi}_{\mathrm{2}} \left(−\mathrm{y}\right)\:+\:\mathrm{C} \\ $$$$\Delta=\mathrm{i}\left(\pi\mathrm{u}\:+\:\mathrm{Li}_{\mathrm{2}} \left(\mathrm{e}^{−\mathrm{2iu}} \right)\:−\:\mathrm{Li}_{\mathrm{2}} \left(−\mathrm{e}^{−\mathrm{2iu}} \right)\right)+\:\mathrm{C} \\ $$$$\Omega=\:\mathrm{xln}\mid\mathrm{tan}\left(\frac{\mathrm{x}}{\mathrm{2}}\right)\mid−\mathrm{i}\left(\frac{\pi\mathrm{x}}{\mathrm{2}}\:+\:\mathrm{Li}_{\mathrm{2}} \left(\mathrm{e}^{−\mathrm{ix}} \right)\:−\:\mathrm{Li}_{\mathrm{2}} \left(−\mathrm{e}^{\mathrm{ix}} \right)\right)\:+\:\mathrm{C} \\ $$$$\mathrm{Check}\:\mathrm{for}\:\mathrm{errors}! \\ $$
Commented by bemath last updated on 19/Oct/20
thank you sir
$${thank}\:{you}\:{sir}\: \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *