Question Number 118868 by bemath last updated on 20/Oct/20

$${If}\:{the}\:{graphs}\:{of}\:{y}={x}^{\mathrm{2}} +\mathrm{2}{ax}+\mathrm{6}{b}\: \\ $$$${and}\:{y}={x}^{\mathrm{2}} +\mathrm{2}{bx}+\mathrm{6}{a}\:{intersect}\:{at}? \\ $$$${only}\:{one}\:{point}\:{in}\:{the}\:{xy}−{plane} \\ $$$$,\:{what}\:{is}\:{the}\:{x}−{coordinate}\:{of}\:{the} \\ $$$${point}\:{of}\:{intersection}\:? \\ $$
Answered by bobhans last updated on 20/Oct/20
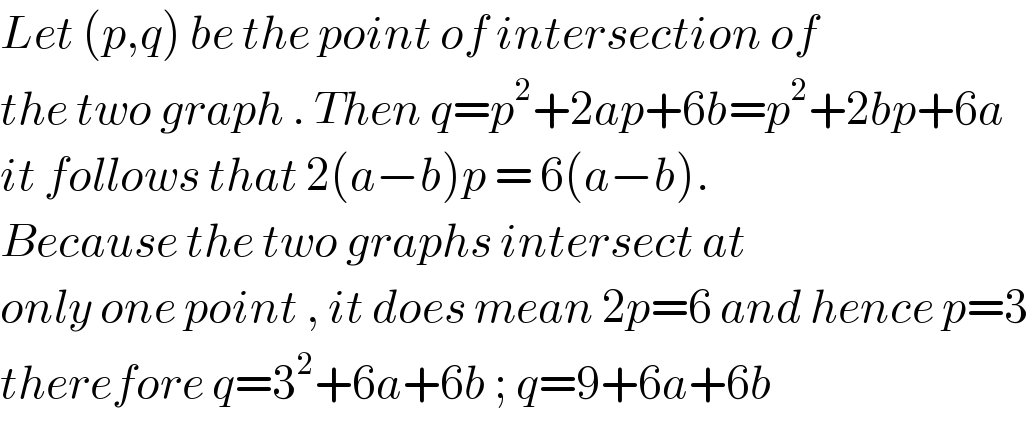
$${Let}\:\left({p},{q}\right)\:{be}\:{the}\:{point}\:{of}\:{intersection}\:{of} \\ $$$${the}\:{two}\:{graph}\:.\:{Then}\:{q}={p}^{\mathrm{2}} +\mathrm{2}{ap}+\mathrm{6}{b}={p}^{\mathrm{2}} +\mathrm{2}{bp}+\mathrm{6}{a} \\ $$$${it}\:{follows}\:{that}\:\mathrm{2}\left({a}−{b}\right){p}\:=\:\mathrm{6}\left({a}−{b}\right). \\ $$$${Because}\:{the}\:{two}\:{graphs}\:{intersect}\:{at} \\ $$$${only}\:{one}\:{point}\:,\:{it}\:{does}\:{mean}\:\mathrm{2}{p}=\mathrm{6}\:{and}\:{hence}\:{p}=\mathrm{3} \\ $$$${therefore}\:{q}=\mathrm{3}^{\mathrm{2}} +\mathrm{6}{a}+\mathrm{6}{b}\:;\:{q}=\mathrm{9}+\mathrm{6}{a}+\mathrm{6}{b} \\ $$
