Menu Close

Question-53422

Tinku Tara 0 Comments
Pin




Question Number 53422 by ajfour last updated on 21/Jan/19
Commented by ajfour last updated on 21/Jan/19
Find maximum inradius and minimum circumradius in terms of a and b if AB of △ABC is variable.
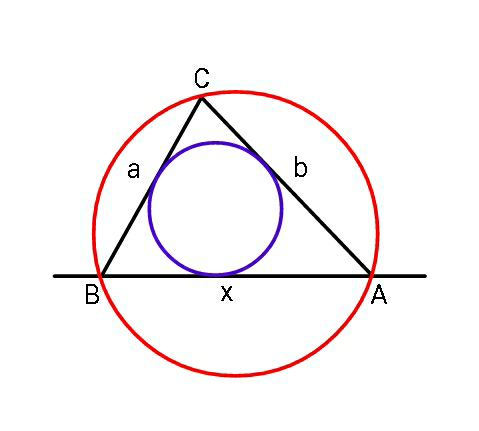
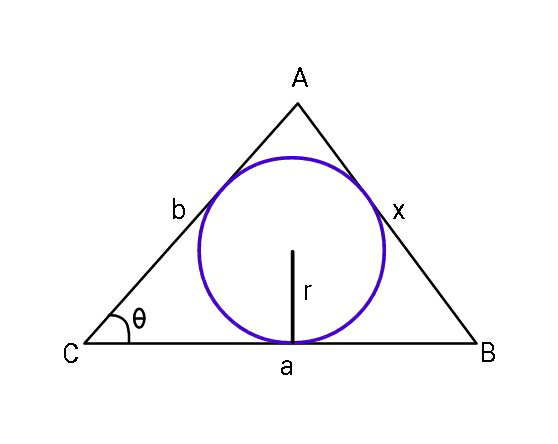
$${Find}\:{maximum}\:{inradius}\:{and} \\ $$$${minimum}\:{circumradius}\:{in}\:{terms} \\ $$$${of}\:{a}\:{and}\:{b}\:{if}\:{AB}\:{of}\:\bigtriangleup{ABC}\:{is}\:{variable}. \\ $$
Commented by mr W last updated on 21/Jan/19
very very nice question sir!
$${very}\:{very}\:{nice}\:{question}\:{sir}! \\ $$
Answered by mr W last updated on 21/Jan/19
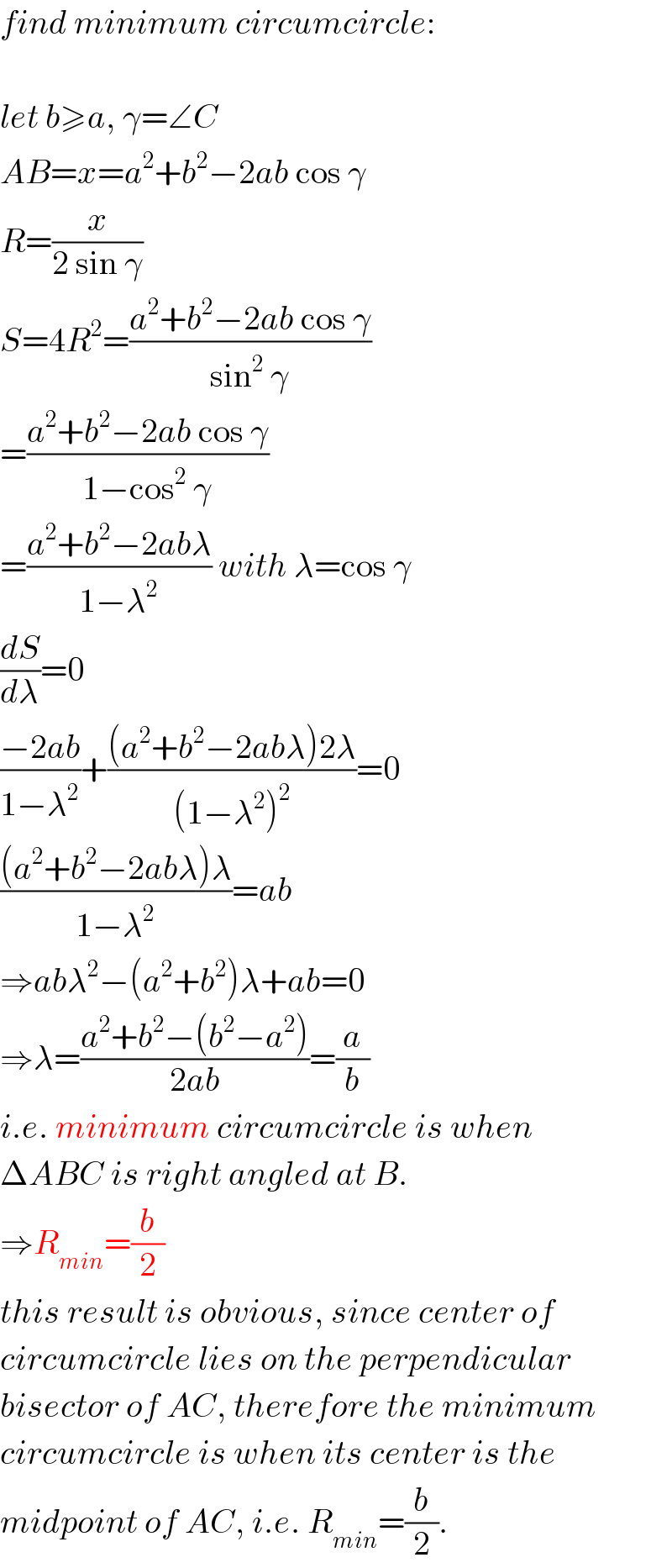
find minimum circumcircle: let b≥a, γ=∠C AB=x=a^2 +b^2 −2ab cos γ R=(x/(2 sin γ)) S=4R^2 =((a^2 +b^2 −2ab cos γ)/(sin^2 γ)) =((a^2 +b^2 −2ab cos γ)/(1−cos^2 γ)) =((a^2 +b^2 −2abλ)/(1−λ^2 )) with λ=cos γ (dS/dλ)=0 ((−2ab)/(1−λ^2 ))+(((a^2 +b^2 −2abλ)2λ)/((1−λ^2 )^2 ))=0 (((a^2 +b^2 −2abλ)λ)/(1−λ^2 ))=ab ⇒abλ^2 −(a^2 +b^2 )λ+ab=0 ⇒λ=((a^2 +b^2 −(b^2 −a^2 ))/(2ab))=(a/b) i.e. minimum circumcircle is when ΔABC is right angled at B. ⇒R_(min) =(b/2) this result is obvious, since center of circumcircle lies on the perpendicular bisector of AC, therefore the minimum circumcircle is when its center is the midpoint of AC, i.e. R_(min) =(b/2).
$${find}\:{minimum}\:{circumcircle}: \\ $$$$ \\ $$$${let}\:{b}\geqslant{a},\:\gamma=\angle{C} \\ $$$${AB}={x}={a}^{\mathrm{2}} +{b}^{\mathrm{2}} −\mathrm{2}{ab}\:\mathrm{cos}\:\gamma \\ $$$${R}=\frac{{x}}{\mathrm{2}\:\mathrm{sin}\:\gamma} \\ $$$${S}=\mathrm{4}{R}^{\mathrm{2}} =\frac{{a}^{\mathrm{2}} +{b}^{\mathrm{2}} −\mathrm{2}{ab}\:\mathrm{cos}\:\gamma}{\mathrm{sin}^{\mathrm{2}} \:\gamma} \\ $$$$=\frac{{a}^{\mathrm{2}} +{b}^{\mathrm{2}} −\mathrm{2}{ab}\:\mathrm{cos}\:\gamma}{\mathrm{1}−\mathrm{cos}^{\mathrm{2}} \:\gamma} \\ $$$$=\frac{{a}^{\mathrm{2}} +{b}^{\mathrm{2}} −\mathrm{2}{ab}\lambda}{\mathrm{1}−\lambda^{\mathrm{2}} }\:{with}\:\lambda=\mathrm{cos}\:\gamma \\ $$$$\frac{{dS}}{{d}\lambda}=\mathrm{0} \\ $$$$\frac{−\mathrm{2}{ab}}{\mathrm{1}−\lambda^{\mathrm{2}} }+\frac{\left({a}^{\mathrm{2}} +{b}^{\mathrm{2}} −\mathrm{2}{ab}\lambda\right)\mathrm{2}\lambda}{\left(\mathrm{1}−\lambda^{\mathrm{2}} \right)^{\mathrm{2}} }=\mathrm{0} \\ $$$$\frac{\left({a}^{\mathrm{2}} +{b}^{\mathrm{2}} −\mathrm{2}{ab}\lambda\right)\lambda}{\mathrm{1}−\lambda^{\mathrm{2}} }={ab} \\ $$$$\Rightarrow{ab}\lambda^{\mathrm{2}} −\left({a}^{\mathrm{2}} +{b}^{\mathrm{2}} \right)\lambda+{ab}=\mathrm{0} \\ $$$$\Rightarrow\lambda=\frac{{a}^{\mathrm{2}} +{b}^{\mathrm{2}} −\left({b}^{\mathrm{2}} −{a}^{\mathrm{2}} \right)}{\mathrm{2}{ab}}=\frac{{a}}{{b}} \\ $$$${i}.{e}.\:{minimum}\:{circumcircle}\:{is}\:{when} \\ $$$$\Delta{ABC}\:{is}\:{right}\:{angled}\:{at}\:{B}. \\ $$$$\Rightarrow{R}_{{min}} =\frac{{b}}{\mathrm{2}} \\ $$$${this}\:{result}\:{is}\:{obvious},\:{since}\:{center}\:{of} \\ $$$${circumcircle}\:{lies}\:{on}\:{the}\:{perpendicular} \\ $$$${bisector}\:{of}\:{AC},\:{therefore}\:{the}\:{minimum} \\ $$$${circumcircle}\:{is}\:{when}\:{its}\:{center}\:{is}\:{the} \\ $$$${midpoint}\:{of}\:{AC},\:{i}.{e}.\:{R}_{{min}} =\frac{{b}}{\mathrm{2}}. \\ $$
Commented by ajfour last updated on 21/Jan/19
Thanks for a great solution and the correction, Sir.
$${Thanks}\:{for}\:{a}\:{great}\:{solution}\:{and}\:{the} \\ $$$${correction},\:{Sir}. \\ $$
Answered by ajfour last updated on 21/Jan/19
Answered by mr W last updated on 22/Jan/19
find maximum incircle: Δ=((ab sin γ)/2)=(((a+b+x)r)/2) ⇒r=((ab sin γ)/(a+b+x))=((ab sin γ)/(a+b+(√(a^2 +b^2 −2ab cos γ)))) (dr/dγ)=0 cos γ=((ab sin^2 γ)/(a^2 +b^2 −2ab cos γ+(a+b)(√(a^2 +b^2 −2ab cos γ)))) cos γ=((sin^2 γ)/((((a+b)^2 )/(ab))−2(1+cos γ)+(((a+b)^2 )/(ab))(√(1−((2(1+cos γ))/(((a+b)^2 )/(ab))))))) with μ=(((a+b)^2 )/(ab)), λ=cos γ ⇒μ−2(1+λ)+(√(μ[μ−2(1+λ)]))=(1/λ)−λ ⇒λ=λ(μ).... examples: a=4, b=4⇒γ=76.3454° a=4, b=3⇒γ=76.9848° a=4, b=2⇒γ=79.3510°
$${find}\:{maximum}\:{incircle}: \\ $$$$\Delta=\frac{{ab}\:\mathrm{sin}\:\gamma}{\mathrm{2}}=\frac{\left({a}+{b}+{x}\right){r}}{\mathrm{2}} \\ $$$$\Rightarrow{r}=\frac{{ab}\:\mathrm{sin}\:\gamma}{{a}+{b}+{x}}=\frac{{ab}\:\mathrm{sin}\:\gamma}{{a}+{b}+\sqrt{{a}^{\mathrm{2}} +{b}^{\mathrm{2}} −\mathrm{2}{ab}\:\mathrm{cos}\:\gamma}} \\ $$$$\frac{{dr}}{{d}\gamma}=\mathrm{0} \\ $$$$\mathrm{cos}\:\gamma=\frac{{ab}\:\mathrm{sin}^{\mathrm{2}} \:\gamma}{{a}^{\mathrm{2}} +{b}^{\mathrm{2}} −\mathrm{2}{ab}\:\mathrm{cos}\:\gamma+\left({a}+{b}\right)\sqrt{{a}^{\mathrm{2}} +{b}^{\mathrm{2}} −\mathrm{2}{ab}\:\mathrm{cos}\:\gamma}} \\ $$$$\mathrm{cos}\:\gamma=\frac{\mathrm{sin}^{\mathrm{2}} \:\gamma}{\frac{\left({a}+{b}\right)^{\mathrm{2}} }{{ab}}−\mathrm{2}\left(\mathrm{1}+\mathrm{cos}\:\gamma\right)+\frac{\left({a}+{b}\right)^{\mathrm{2}} }{{ab}}\sqrt{\mathrm{1}−\frac{\mathrm{2}\left(\mathrm{1}+\mathrm{cos}\:\gamma\right)}{\frac{\left({a}+{b}\right)^{\mathrm{2}} }{{ab}}}}} \\ $$$${with}\:\mu=\frac{\left({a}+{b}\right)^{\mathrm{2}} }{{ab}},\:\lambda=\mathrm{cos}\:\gamma \\ $$$$\Rightarrow\mu−\mathrm{2}\left(\mathrm{1}+\lambda\right)+\sqrt{\mu\left[\mu−\mathrm{2}\left(\mathrm{1}+\lambda\right)\right]}=\frac{\mathrm{1}}{\lambda}−\lambda \\ $$$$\Rightarrow\lambda=\lambda\left(\mu\right)…. \\ $$$$ \\ $$$${examples}: \\ $$$${a}=\mathrm{4},\:{b}=\mathrm{4}\Rightarrow\gamma=\mathrm{76}.\mathrm{3454}° \\ $$$${a}=\mathrm{4},\:{b}=\mathrm{3}\Rightarrow\gamma=\mathrm{76}.\mathrm{9848}° \\ $$$${a}=\mathrm{4},\:{b}=\mathrm{2}\Rightarrow\gamma=\mathrm{79}.\mathrm{3510}° \\ $$
Commented by mr W last updated on 21/Jan/19
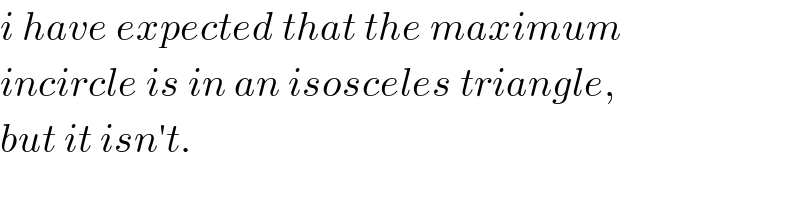
i have expected that the maximum incircle is in an isosceles triangle, but it isn′t.
$${i}\:{have}\:{expected}\:{that}\:{the}\:{maximum} \\ $$$${incircle}\:{is}\:{in}\:{an}\:{isosceles}\:{triangle}, \\ $$$${but}\:{it}\:{isn}'{t}. \\ $$
Commented by ajfour last updated on 21/Jan/19
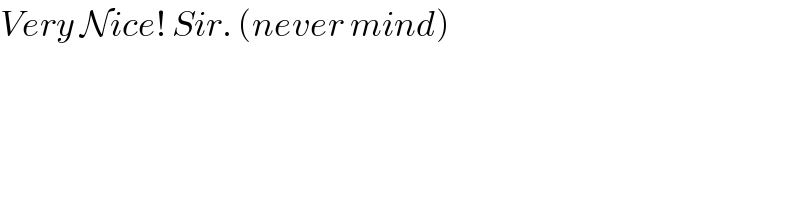
Very Nice! Sir. (never mind)
$${Very}\:\mathcal{N}{ice}!\:{Sir}.\:\left({never}\:{mind}\right) \\ $$
Answered by MJS last updated on 23/Jan/19
the maximum incircle is at x=((a+b)/3)(−1+4sin ((1/3)(π+arcsin ((4a^2 −19ab+4b^2 )/(4(a+b)^2 )))))
$$\mathrm{the}\:\mathrm{maximum}\:\mathrm{incircle}\:\mathrm{is}\:\mathrm{at} \\ $$$${x}=\frac{{a}+{b}}{\mathrm{3}}\left(−\mathrm{1}+\mathrm{4sin}\:\left(\frac{\mathrm{1}}{\mathrm{3}}\left(\pi+\mathrm{arcsin}\:\frac{\mathrm{4}{a}^{\mathrm{2}} −\mathrm{19}{ab}+\mathrm{4}{b}^{\mathrm{2}} }{\mathrm{4}\left({a}+{b}\right)^{\mathrm{2}} }\right)\right)\right) \\ $$
Commented by mr W last updated on 22/Jan/19
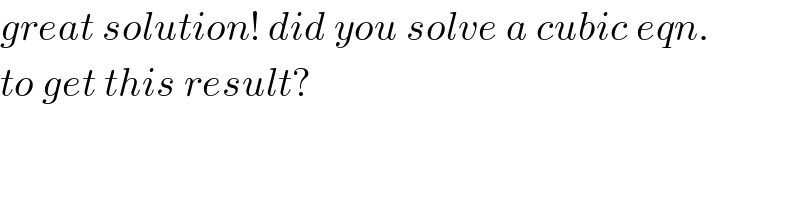
great solution! did you solve a cubic eqn. to get this result?
$${great}\:{solution}!\:{did}\:{you}\:{solve}\:{a}\:{cubic}\:{eqn}. \\ $$$${to}\:{get}\:{this}\:{result}? \\ $$
Commented by MJS last updated on 23/Jan/19
yes Sir. I took Heron′s formula for the incircle and set it′s derivate =0 just to see if it′s possible to go this way... and it has been possible!
$$\mathrm{yes}\:\mathrm{Sir}.\:\mathrm{I}\:\mathrm{took}\:\mathrm{Heron}'\mathrm{s}\:\mathrm{formula}\:\mathrm{for}\:\mathrm{the} \\ $$$$\mathrm{incircle}\:\mathrm{and}\:\mathrm{set}\:\mathrm{it}'\mathrm{s}\:\mathrm{derivate}\:=\mathrm{0}\:\mathrm{just}\:\mathrm{to}\:\mathrm{see} \\ $$$$\mathrm{if}\:\mathrm{it}'\mathrm{s}\:\mathrm{possible}\:\mathrm{to}\:\mathrm{go}\:\mathrm{this}\:\mathrm{way}…\:\mathrm{and}\:\mathrm{it}\:\mathrm{has} \\ $$$$\mathrm{been}\:\mathrm{possible}! \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *