Menu Close

Calculate-the-number-of-ways-in-which-a-5-children-can-be-divided-into-groups-of-2-and-3-b-9-children-can-be-divided-into-groups-of-5-and-4-Hence-calculate-the-number-of-ways-in-which-9-childre

Tinku Tara 0 Comments
Pin




Question Number 5254 by Rasheed Soomro last updated on 02/May/16
Calculate the number of ways in which (a) 5 children can be divided into groups of 2 and 3 , (b) 9 children can be divided into groups of 5 and 4, Hence calculate the number of ways in which 9 children can be divided into groups of 2,3 and 4.
$$\mathrm{Calculate}\:\mathrm{the}\:\mathrm{number}\:\mathrm{of}\:\mathrm{ways}\:\mathrm{in}\:\mathrm{which} \\ $$$$\left(\boldsymbol{\mathrm{a}}\right)\:\mathrm{5}\:\mathrm{children}\:\mathrm{can}\:\mathrm{be}\:\mathrm{divided}\:\mathrm{into}\:\mathrm{groups} \\ $$$$\mathrm{of}\:\mathrm{2}\:\mathrm{and}\:\mathrm{3}\:, \\ $$$$\left(\boldsymbol{\mathrm{b}}\right)\:\mathrm{9}\:\mathrm{children}\:\mathrm{can}\:\mathrm{be}\:\mathrm{divided}\:\mathrm{into}\:\mathrm{groups} \\ $$$$\mathrm{of}\:\mathrm{5}\:\mathrm{and}\:\mathrm{4}, \\ $$$$\mathrm{Hence}\:\mathrm{calculate}\:\mathrm{the}\:\mathrm{number}\:\mathrm{of}\:\mathrm{ways}\:\mathrm{in} \\ $$$$\mathrm{which}\:\mathrm{9}\:\mathrm{children}\:\mathrm{can}\:\mathrm{be}\:\mathrm{divided}\:\mathrm{into} \\ $$$$\mathrm{groups}\:\mathrm{of}\:\mathrm{2},\mathrm{3}\:\mathrm{and}\:\mathrm{4}. \\ $$
Commented by prakash jain last updated on 02/May/16
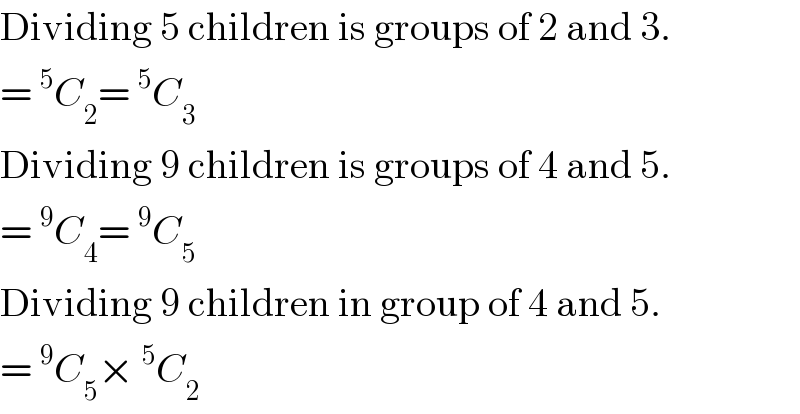
Dividing 5 children is groups of 2 and 3. =^5 C_2 =^5 C_3 Dividing 9 children is groups of 4 and 5. =^9 C_4 =^9 C_5 Dividing 9 children in group of 4 and 5. =^9 C_5 ×^5 C_2
$$\mathrm{Dividing}\:\mathrm{5}\:\mathrm{children}\:\mathrm{is}\:\mathrm{groups}\:\mathrm{of}\:\mathrm{2}\:\mathrm{and}\:\mathrm{3}. \\ $$$$=\:^{\mathrm{5}} {C}_{\mathrm{2}} =\:^{\mathrm{5}} {C}_{\mathrm{3}} \\ $$$$\mathrm{Dividing}\:\mathrm{9}\:\mathrm{children}\:\mathrm{is}\:\mathrm{groups}\:\mathrm{of}\:\mathrm{4}\:\mathrm{and}\:\mathrm{5}. \\ $$$$=\:^{\mathrm{9}} {C}_{\mathrm{4}} =\:^{\mathrm{9}} {C}_{\mathrm{5}} \\ $$$$\mathrm{Dividing}\:\mathrm{9}\:\mathrm{children}\:\mathrm{in}\:\mathrm{group}\:\mathrm{of}\:\mathrm{4}\:\mathrm{and}\:\mathrm{5}. \\ $$$$=\:^{\mathrm{9}} {C}_{\mathrm{5}} ×\:^{\mathrm{5}} {C}_{\mathrm{2}} \\ $$
Answered by Yozzii last updated on 02/May/16
(a) no. of ways= ((5),(2) )= ((5),(3) ) This is because by creating a group of 2 children you simultaneously yield a second group of 3 children corresponding to the group of two children chosen. The answer of ((5),(3) ) shows the converse where 3 children are chosen. (b) no. of ways= ((9),(4) )= ((9),(5) ) To divide 9 children into groups of 2,3 and 4 you can first choose 4 out of 9 ⇒ ((9),(4) ) ways. This leaves a group of 4 and a group of 5. Then, to split 5 into groups of 2 and 3⇒ ((5),(3) ) ways. By the AND principle of counting we must have the event of choosing 4 children and the event of spliting 5 children into groups of 2 and 3 at the same time, in ((9),(4) )× ((5),(3) )=1260 ways.
$$\left(\boldsymbol{\mathrm{a}}\right)\:\mathrm{no}.\:\mathrm{of}\:\mathrm{ways}=\begin{pmatrix}{\mathrm{5}}\\{\mathrm{2}}\end{pmatrix}=\begin{pmatrix}{\mathrm{5}}\\{\mathrm{3}}\end{pmatrix} \\ $$$${This}\:{is}\:{because}\:{by}\:{creating}\:{a}\:{group}\:{of} \\ $$$$\mathrm{2}\:{children}\:{you}\:{simultaneously} \\ $$$${yield}\:{a}\:{second}\:{group}\:{of}\:\mathrm{3}\:{children} \\ $$$${corresponding}\:{to}\:{the}\:{group}\:{of}\:{two}\:{children}\:{chosen}. \\ $$$${The}\:{answer}\:{of}\:\:\begin{pmatrix}{\mathrm{5}}\\{\mathrm{3}}\end{pmatrix}\:{shows}\:{the}\:{converse} \\ $$$${where}\:\mathrm{3}\:{children}\:{are}\:{chosen}. \\ $$$$\left(\boldsymbol{\mathrm{b}}\right)\:\mathrm{no}.\:\mathrm{of}\:\mathrm{ways}=\begin{pmatrix}{\mathrm{9}}\\{\mathrm{4}}\end{pmatrix}=\begin{pmatrix}{\mathrm{9}}\\{\mathrm{5}}\end{pmatrix} \\ $$$$ \\ $$$${To}\:{divide}\:\mathrm{9}\:{children}\:{into}\:{groups}\:{of} \\ $$$$\mathrm{2},\mathrm{3}\:{and}\:\mathrm{4}\:{you}\:{can}\:{first}\:{choose}\: \\ $$$$\mathrm{4}\:{out}\:{of}\:\mathrm{9}\:\Rightarrow\begin{pmatrix}{\mathrm{9}}\\{\mathrm{4}}\end{pmatrix}\:{ways}.\:\:{This}\:{leaves}\:{a}\: \\ $$$${group}\:{of}\:\mathrm{4}\:{and}\:{a}\:{group}\:{of}\:\mathrm{5}.\:{Then},\:{to} \\ $$$${split}\:\mathrm{5}\:{into}\:{groups}\:{of}\:\mathrm{2}\:{and}\:\mathrm{3}\Rightarrow\begin{pmatrix}{\mathrm{5}}\\{\mathrm{3}}\end{pmatrix}\:{ways}. \\ $$$${By}\:{the}\:{AND}\:{principle}\:{of}\:{counting} \\ $$$${we}\:{must}\:{have}\:{the}\:{event}\:{of}\:{choosing} \\ $$$$\mathrm{4}\:{children}\:{and}\:{the}\:{event}\:{of}\:{spliting} \\ $$$$\mathrm{5}\:{children}\:{into}\:{groups}\:{of}\:\mathrm{2}\:{and}\:\mathrm{3} \\ $$$${at}\:{the}\:{same}\:{time},\:{in}\:\begin{pmatrix}{\mathrm{9}}\\{\mathrm{4}}\end{pmatrix}×\begin{pmatrix}{\mathrm{5}}\\{\mathrm{3}}\end{pmatrix}=\mathrm{1260}\:{ways}. \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *