Question Number 53468 by ajfour last updated on 22/Jan/19
Commented by ajfour last updated on 22/Jan/19
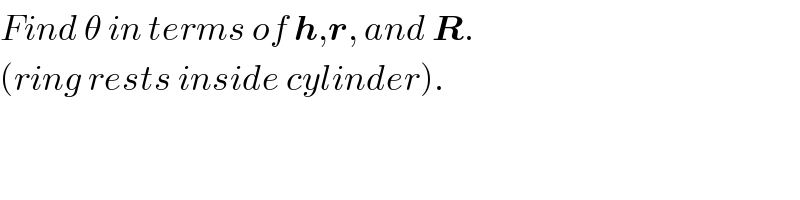
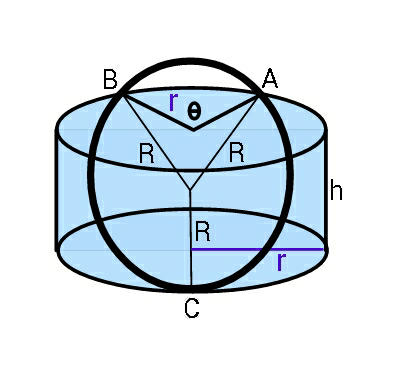
$${Find}\:\theta\:{in}\:{terms}\:{of}\:\boldsymbol{{h}},\boldsymbol{{r}},\:{and}\:\boldsymbol{{R}}. \\ $$$$\left({ring}\:{rests}\:{inside}\:{cylinder}\right).\:\:\: \\ $$
Commented by mr W last updated on 23/Jan/19

$${please}\:{check}\:{sir}: \\ $$$${such}\:{that}\:{the}\:{ring}\:{can}\:{be}\:{placed}\:{into} \\ $$$${the}\:{cylinder}\Rightarrow{R}\leqslant{r} \\ $$$${but}\:{if}\:{R}\leqslant{r}\Rightarrow{the}\:{ring}\:{can}\:{not}\:{rest}\:{on} \\ $$$${the}\:{cylinder}. \\ $$$$\Rightarrow{no}\:{solution}? \\ $$
Commented by ajfour last updated on 23/Jan/19
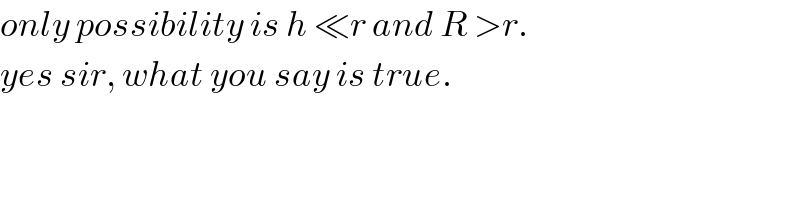
$${only}\:{possibility}\:{is}\:{h}\:\ll{r}\:{and}\:{R}\:>{r}. \\ $$$${yes}\:{sir},\:{what}\:{you}\:{say}\:{is}\:{true}. \\ $$
Answered by mr W last updated on 23/Jan/19

$${AB}=\mathrm{2}{b}=\mathrm{2}{r}\:\mathrm{sin}\:\frac{\theta}{\mathrm{2}} \\ $$$$\Rightarrow{b}={r}\:\mathrm{sin}\:\frac{\theta}{\mathrm{2}} \\ $$$$\left({r}+\sqrt{{r}^{\mathrm{2}} −{b}^{\mathrm{2}} }\right)^{\mathrm{2}} +{h}^{\mathrm{2}} =\left({R}+\sqrt{{R}^{\mathrm{2}} −{b}^{\mathrm{2}} }\right)^{\mathrm{2}} \\ $$$$\Rightarrow{R}\sqrt{{R}^{\mathrm{2}} −{b}^{\mathrm{2}} }−{r}\sqrt{{r}^{\mathrm{2}} −{b}^{\mathrm{2}} }=\frac{{h}^{\mathrm{2}} }{\mathrm{2}}−\left({R}^{\mathrm{2}} −{r}^{\mathrm{2}} \right) \\ $$$$\Rightarrow\frac{{R}}{{r}}\sqrt{\frac{{R}^{\mathrm{2}} }{{r}^{\mathrm{2}} }−\mathrm{sin}^{\mathrm{2}} \:\frac{\theta}{\mathrm{2}}}−\mathrm{cos}\:\frac{\theta}{\mathrm{2}}=\frac{{h}^{\mathrm{2}} }{\mathrm{2}{r}^{\mathrm{2}} }−\frac{{R}^{\mathrm{2}} }{{r}^{\mathrm{2}} }+\mathrm{1} \\ $$$${with}\:\mu=\frac{{R}}{{r}},\:\eta=\frac{{h}}{\:\sqrt{\mathrm{2}}{r}} \\ $$$$\Rightarrow\mu^{\mathrm{2}} +\mu\sqrt{\mu^{\mathrm{2}} −\mathrm{1}+\mathrm{cos}^{\mathrm{2}} \:\frac{\theta}{\mathrm{2}}}−\mathrm{cos}\:\frac{\theta}{\mathrm{2}}=\mathrm{1}+\eta^{\mathrm{2}} \\ $$$$\Rightarrow\mathrm{cos}\:\frac{\theta}{\mathrm{2}}=…. \\ $$
