Menu Close

Given-point-A-7-26-and-B-12-12-find-all-points-P-such-that-AP-BP-and-APB-90-

Tinku Tara 0 Comments
Pin




Question Number 119007 by bramlexs22 last updated on 21/Oct/20
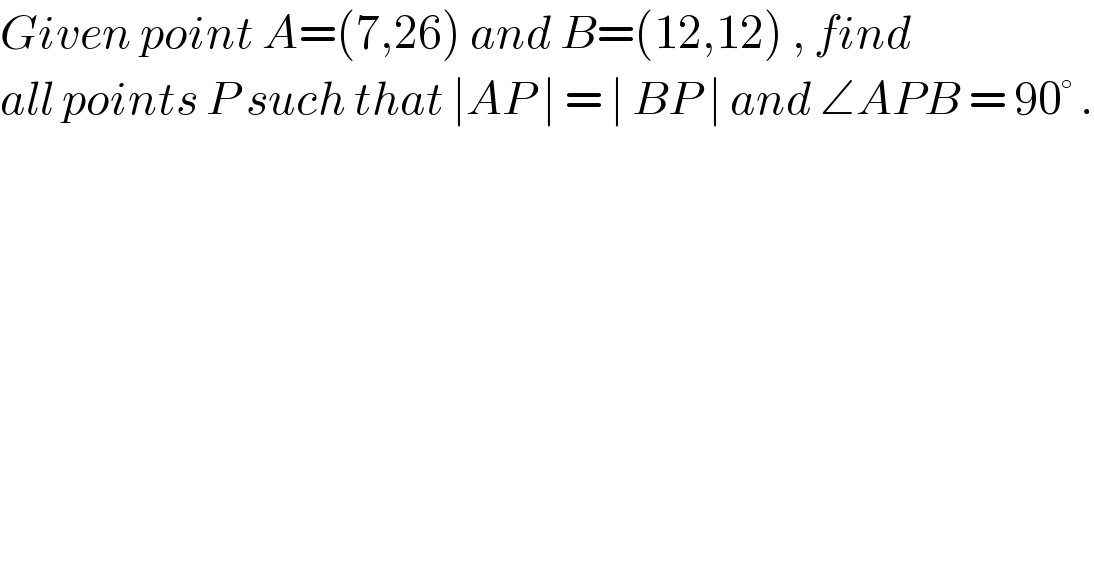
Given point A=(7,26) and B=(12,12) , find all points P such that ∣AP ∣ = ∣ BP ∣ and ∠APB = 90° .
$${Given}\:{point}\:{A}=\left(\mathrm{7},\mathrm{26}\right)\:{and}\:{B}=\left(\mathrm{12},\mathrm{12}\right)\:,\:{find} \\ $$$${all}\:{points}\:{P}\:{such}\:{that}\:\mid{AP}\:\mid\:=\:\mid\:{BP}\:\mid\:{and}\:\angle{APB}\:=\:\mathrm{90}°\:. \\ $$
Answered by bemath last updated on 21/Oct/20
Note that the triangle ABP is an isosceles right triangle with ∣AP ∣ = ∣BP ∣. Let Q be the midpoint of segment AB. Then Q=(((19)/2) ,19), where ∣QA∣ = ∣QB∣ = ∣QP ∣ and QA ⊥ QB Thus Q^→ A^→ = ((5/2),−7) and Q^→ P = (7,(5/2)) or (−7,−(5/2)). Let O=(0,0) be the origin , it follows that OP^→ = OQ^→ + QP^→ = (((19)/2), 19) ±(7,(5/2)). Consequently P = (((33)/2), ((43)/2)) or ((5/2), ((33)/2))
$$\:{Note}\:{that}\:{the}\:{triangle}\:{ABP}\:{is}\:{an}\:{isosceles}\:{right} \\ $$$${triangle}\:{with}\:\mid{AP}\:\mid\:=\:\mid{BP}\:\mid.\:{Let}\:{Q}\:{be}\:{the}\:{midpoint} \\ $$$${of}\:{segment}\:{AB}.\:{Then}\:{Q}=\left(\frac{\mathrm{19}}{\mathrm{2}}\:,\mathrm{19}\right),\:{where} \\ $$$$\mid{QA}\mid\:=\:\mid{QB}\mid\:=\:\mid{QP}\:\mid\:\:{and}\:{QA}\:\bot\:{QB} \\ $$$${Thus}\:\overset{\rightarrow} {{Q}}\overset{\rightarrow} {{A}}\:=\:\left(\frac{\mathrm{5}}{\mathrm{2}},−\mathrm{7}\right)\:{and}\:\overset{\rightarrow} {{Q}P}\:=\:\left(\mathrm{7},\frac{\mathrm{5}}{\mathrm{2}}\right)\: \\ $$$${or}\:\left(−\mathrm{7},−\frac{\mathrm{5}}{\mathrm{2}}\right).\:{Let}\:{O}=\left(\mathrm{0},\mathrm{0}\right)\:{be}\:{the}\:{origin}\:,\:{it}\:{follows}\:{that} \\ $$$${O}\overset{\rightarrow} {{P}}\:=\:{O}\overset{\rightarrow} {{Q}}\:+\:{Q}\overset{\rightarrow} {{P}}\:=\:\left(\frac{\mathrm{19}}{\mathrm{2}},\:\mathrm{19}\right)\:\pm\left(\mathrm{7},\frac{\mathrm{5}}{\mathrm{2}}\right). \\ $$$${Consequently}\:{P}\:=\:\left(\frac{\mathrm{33}}{\mathrm{2}},\:\frac{\mathrm{43}}{\mathrm{2}}\right)\:{or}\:\left(\frac{\mathrm{5}}{\mathrm{2}},\:\frac{\mathrm{33}}{\mathrm{2}}\right) \\ $$
Answered by 1549442205PVT last updated on 21/Oct/20
AB^(→) =(5,−14) Midpoint of AB is M(((19)/2),19),AP=BP ⇒P(x,y) lying on the midline d of AB,so MP^(→) =(((19)/2)−x,19−y) perpendicular to AB^(→) ⇔AB^(→) .MP^(→) =0⇔5(((19)/2)−x)−14(19−y)=0 ⇔5x−14y+218.5=0⇒P(x,((5x+218.5)/(14))) AP^(→) =(x−7,((5x−145.5)/(14))),BP^(→) =(x−12,((5x+50.5)/(14))) APB^(�) =90°⇔AP^(→) ⊥BP^(→) ⇔AP^(→) .BP^(→) =0 ⇔(x−7)(x−12)+(((5x−145.5)/(14)))(((5x+50.5)/(14)))=0 x^2 −19x+84+((25x^2 −475x−7347.25)/(196))=0 221x^2 −4199x+9116.75=0 x_1 =16.5,x_2 =2.5.We get two the pointP P_1 (16.5,((43)/2)),P_2 (2.5,((33)/2))
$$\overset{\rightarrow} {\mathrm{AB}}=\left(\mathrm{5},−\mathrm{14}\right) \\ $$$$\mathrm{Midpoint}\:\mathrm{of}\:\mathrm{AB}\:\mathrm{is}\:\mathrm{M}\left(\frac{\mathrm{19}}{\mathrm{2}},\mathrm{19}\right),\mathrm{AP}=\mathrm{BP} \\ $$$$\Rightarrow\mathrm{P}\left(\mathrm{x},\mathrm{y}\right)\:\mathrm{lying}\:\mathrm{on}\:\mathrm{the}\:\mathrm{midline}\:\mathrm{d}\:\mathrm{of}\:\mathrm{AB},\mathrm{so} \\ $$$$\overset{\rightarrow} {\mathrm{MP}}=\left(\frac{\mathrm{19}}{\mathrm{2}}−\mathrm{x},\mathrm{19}−\mathrm{y}\right)\:\mathrm{perpendicular}\:\mathrm{to} \\ $$$$\overset{\rightarrow} {\mathrm{AB}}\Leftrightarrow\overset{\rightarrow} {\mathrm{AB}}.\overset{\rightarrow} {\mathrm{MP}}=\mathrm{0}\Leftrightarrow\mathrm{5}\left(\frac{\mathrm{19}}{\mathrm{2}}−\mathrm{x}\right)−\mathrm{14}\left(\mathrm{19}−\mathrm{y}\right)=\mathrm{0} \\ $$$$\Leftrightarrow\mathrm{5x}−\mathrm{14y}+\mathrm{218}.\mathrm{5}=\mathrm{0}\Rightarrow\mathrm{P}\left(\mathrm{x},\frac{\mathrm{5x}+\mathrm{218}.\mathrm{5}}{\mathrm{14}}\right) \\ $$$$\overset{\rightarrow} {\mathrm{AP}}=\left(\mathrm{x}−\mathrm{7},\frac{\mathrm{5x}−\mathrm{145}.\mathrm{5}}{\mathrm{14}}\right),\overset{\rightarrow} {\mathrm{BP}}=\left(\mathrm{x}−\mathrm{12},\frac{\mathrm{5x}+\mathrm{50}.\mathrm{5}}{\mathrm{14}}\right) \\ $$$$\widehat {\mathrm{APB}}=\mathrm{90}°\Leftrightarrow\overset{\rightarrow} {\mathrm{AP}}\bot\overset{\rightarrow} {\mathrm{BP}}\Leftrightarrow\overset{\rightarrow} {\mathrm{AP}}.\overset{\rightarrow} {\mathrm{BP}}=\mathrm{0} \\ $$$$\Leftrightarrow\left(\mathrm{x}−\mathrm{7}\right)\left(\mathrm{x}−\mathrm{12}\right)+\left(\frac{\mathrm{5x}−\mathrm{145}.\mathrm{5}}{\mathrm{14}}\right)\left(\frac{\mathrm{5x}+\mathrm{50}.\mathrm{5}}{\mathrm{14}}\right)=\mathrm{0} \\ $$$$\mathrm{x}^{\mathrm{2}} −\mathrm{19x}+\mathrm{84}+\frac{\mathrm{25x}^{\mathrm{2}} −\mathrm{475x}−\mathrm{7347}.\mathrm{25}}{\mathrm{196}}=\mathrm{0} \\ $$$$\mathrm{221x}^{\mathrm{2}} −\mathrm{4199x}+\mathrm{9116}.\mathrm{75}=\mathrm{0} \\ $$$$\mathrm{x}_{\mathrm{1}} =\mathrm{16}.\mathrm{5},\mathrm{x}_{\mathrm{2}} =\mathrm{2}.\mathrm{5}.\mathrm{We}\:\mathrm{get}\:\mathrm{two}\:\mathrm{the}\:\mathrm{pointP} \\ $$$$\mathrm{P}_{\mathrm{1}} \left(\mathrm{16}.\mathrm{5},\frac{\mathrm{43}}{\mathrm{2}}\right),\mathrm{P}_{\mathrm{2}} \left(\mathrm{2}.\mathrm{5},\frac{\mathrm{33}}{\mathrm{2}}\right) \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *