Question Number 53570 by ajfour last updated on 23/Jan/19

Commented by ajfour last updated on 23/Jan/19

$${Regular}\:{pentagon}\:{side}\:{a}.\:{Find}\:{the} \\ $$$${central}\:{uncoloured}\:{area}. \\ $$
Commented by tanmay.chaudhury50@gmail.com last updated on 23/Jan/19
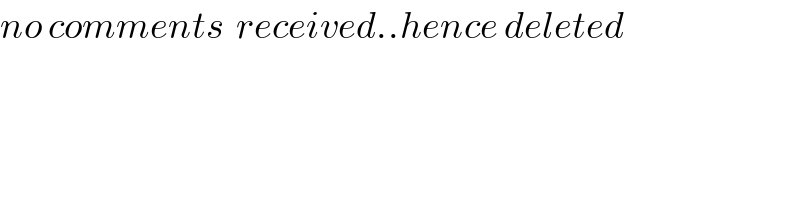
$${no}\:{comments}\:\:{received}..{hence}\:{deleted} \\ $$
Commented by tanmay.chaudhury50@gmail.com last updated on 23/Jan/19

Commented by ajfour last updated on 23/Jan/19
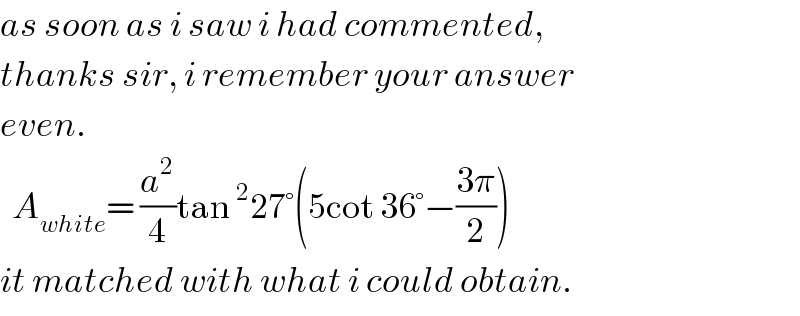
$${as}\:{soon}\:{as}\:{i}\:{saw}\:{i}\:{had}\:{commented}, \\ $$$${thanks}\:{sir},\:{i}\:{remember}\:{your}\:{answer} \\ $$$${even}. \\ $$$$\:\:{A}_{{white}} =\:\frac{{a}^{\mathrm{2}} }{\mathrm{4}}\mathrm{tan}\:^{\mathrm{2}} \mathrm{27}°\left(\mathrm{5cot}\:\mathrm{36}°−\frac{\mathrm{3}\pi}{\mathrm{2}}\right) \\ $$$${it}\:{matched}\:{with}\:{what}\:{i}\:{could}\:{obtain}. \\ $$
Commented by ajfour last updated on 23/Jan/19

$${Tanmay}\:{Sir},\:{why}\:{you}\:{deleted}\:{your} \\ $$$${posted}\:{solution}\:? \\ $$
Commented by tanmay.chaudhury50@gmail.com last updated on 23/Jan/19
![tanα=(r/(a/2)) r=(a/2)tanα....(1) 5θ=2π θ=((2π)/5).....(2) 2β+θ=π β=((π−((2π)/5))/2)=((3π)/(10 ))....(3) now area of small pentagon... 5×(1/2)×2r×h tan(θ/2)=(r/h) so h=rcot(θ/2) so area of small pentagon=5×(1/2)×2r×rcot((θ/2)) area of five sector of circle=5×((πr^2 )/(2π))×2β =5r^2 β so area of white centre star =area of small pentagon−five sector area =5r^2 cot((θ/2))−5r^2 β =5r^2 [cot((θ/2))−β] =5×((a/2)tanα)^2 [cot((θ/2))−β] now θ=((2π)/5) β=((3π)/(10)) to find α... using formula... number of side=((360)/(external angke)) external angke=((360)/5)=72^o internal+external angld=180^o inyernsl angld=180^o −72=108^o 4α=108= so α=27^o hdnce required answer is =★★ 5×((a/2)tanα)^2 [cot((θ/2))−β]★★ =5×((a/2)tan27^o )^2 [cot(((2π)/(5×2)))−((3π)/(10))] =(a^2 /4)tan^2 27^o ×[5cot36^o −((3π)/2)] now pls check...](https://www.tinkutara.com/question/Q53589.png)
$$ \\ $$$${tan}\alpha=\frac{{r}}{\frac{{a}}{\mathrm{2}}}\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:{r}=\frac{{a}}{\mathrm{2}}{tan}\alpha….\left(\mathrm{1}\right) \\ $$$$\mathrm{5}\theta=\mathrm{2}\pi\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\theta=\frac{\mathrm{2}\pi}{\mathrm{5}}…..\left(\mathrm{2}\right) \\ $$$$\mathrm{2}\beta+\theta=\pi\:\:\:\:\:\:\:\:\beta=\frac{\pi−\frac{\mathrm{2}\pi}{\mathrm{5}}}{\mathrm{2}}=\frac{\mathrm{3}\pi}{\mathrm{10}\:}….\left(\mathrm{3}\right) \\ $$$${now}\:{area}\:{of}\:{small}\:{pentagon}… \\ $$$$\mathrm{5}×\frac{\mathrm{1}}{\mathrm{2}}×\mathrm{2}{r}×{h} \\ $$$${tan}\frac{\theta}{\mathrm{2}}=\frac{{r}}{{h}}\:\:{so}\:{h}={rcot}\frac{\theta}{\mathrm{2}} \\ $$$${so}\:{area}\:{of}\:{small}\:{pentagon}=\mathrm{5}×\frac{\mathrm{1}}{\mathrm{2}}×\mathrm{2}{r}×{rcot}\left(\frac{\theta}{\mathrm{2}}\right) \\ $$$${area}\:{of}\:{five}\:{sector}\:{of}\:{circle}=\mathrm{5}×\frac{\pi{r}^{\mathrm{2}} }{\mathrm{2}\pi}×\mathrm{2}\beta \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:=\mathrm{5}{r}^{\mathrm{2}} \beta \\ $$$$\boldsymbol{{so}}\:\boldsymbol{{area}}\:\boldsymbol{{of}}\:\boldsymbol{{white}}\:\boldsymbol{{centre}}\:\boldsymbol{{star}} \\ $$$$=\boldsymbol{{area}}\:\boldsymbol{{of}}\:\boldsymbol{{small}}\:\boldsymbol{{pentagon}}−\boldsymbol{{five}}\:\boldsymbol{{sector}}\:\boldsymbol{{area}} \\ $$$$=\mathrm{5}\boldsymbol{{r}}^{\mathrm{2}} \boldsymbol{{cot}}\left(\frac{\theta}{\mathrm{2}}\right)−\mathrm{5}\boldsymbol{{r}}^{\mathrm{2}} \beta \\ $$$$=\mathrm{5}{r}^{\mathrm{2}} \left[{cot}\left(\frac{\theta}{\mathrm{2}}\right)−\beta\right] \\ $$$$=\mathrm{5}×\left(\frac{{a}}{\mathrm{2}}{tan}\alpha\right)^{\mathrm{2}} \left[{cot}\left(\frac{\theta}{\mathrm{2}}\right)−\beta\right] \\ $$$${now}\:\:\theta=\frac{\mathrm{2}\pi}{\mathrm{5}}\:\:\:\beta=\frac{\mathrm{3}\pi}{\mathrm{10}}\:\: \\ $$$${to}\:{find}\:\alpha… \\ $$$${using}\:{formula}… \\ $$$${number}\:{of}\:{side}=\frac{\mathrm{360}}{{external}\:{angke}} \\ $$$${external}\:{angke}=\frac{\mathrm{360}}{\mathrm{5}}=\mathrm{72}^{{o}} \\ $$$${internal}+{external}\:{angld}=\mathrm{180}^{{o}} \\ $$$${inyernsl}\:{angld}=\mathrm{180}^{{o}} −\mathrm{72}=\mathrm{108}^{{o}} \\ $$$$\mathrm{4}\alpha=\mathrm{108}=\:\:\boldsymbol{{so}}\:\alpha=\mathrm{27}^{{o}} \\ $$$$\boldsymbol{{hdnce}}\:\boldsymbol{{required}}\:\boldsymbol{{answer}}\:\boldsymbol{{is}} \\ $$$$=\bigstar\bigstar\:\mathrm{5}×\left(\frac{{a}}{\mathrm{2}}{tan}\alpha\right)^{\mathrm{2}} \left[{cot}\left(\frac{\theta}{\mathrm{2}}\right)−\beta\right]\bigstar\bigstar \\ $$$$=\mathrm{5}×\left(\frac{{a}}{\mathrm{2}}{tan}\mathrm{27}^{{o}} \right)^{\mathrm{2}} \left[{cot}\left(\frac{\mathrm{2}\pi}{\mathrm{5}×\mathrm{2}}\right)−\frac{\mathrm{3}\pi}{\mathrm{10}}\right] \\ $$$$=\frac{{a}^{\mathrm{2}} }{\mathrm{4}}{tan}^{\mathrm{2}} \mathrm{27}^{{o}} ×\left[\mathrm{5}{cot}\mathrm{36}^{{o}} −\frac{\mathrm{3}\pi}{\mathrm{2}}\right] \\ $$$${now}\:{pls}\:{check}… \\ $$$$ \\ $$
Commented by tanmay.chaudhury50@gmail.com last updated on 23/Jan/19

$${thank}\:{you}.. \\ $$
Answered by mr W last updated on 23/Jan/19

Commented by mr W last updated on 23/Jan/19
![α=((2π)/(10))=(π/5) (r+(r/(sin α)))tan α=(a/2) r=((a cos α)/(2(1+sin α))) A=10[(r^2 /(2 tan α))−(r^2 /2)((π/2)−α)] A=5r^2 [α+(1/(tan α))−(π/2)] A=((5a^2 cos^2 α)/(4(1+sin α)^2 ))[(π/5)+(1/(tan α))−(π/2)] cos α=(((√5)+1)/4) sin α=((√(2(5−(√5))))/4) tan α=(√(5−2(√5))) A=((a^2 cos^2 α)/(8(1+sin α)^2 ))[((10)/(tan α))−3π] A=((a^2 ((√5)+1)^2 )/(8(4+(√(2(5−(√5))))^2 ))[((10(√(5+2(√5))))/( (√5)))−3π] ⇒A=((a^2 (3+(√5))[2(√(5(5+2(√5))))−3π])/(8[13−(√5)+4(√(2(5−(√5))))]))≈0.14081a^2](https://www.tinkutara.com/question/Q53588.png)
$$\alpha=\frac{\mathrm{2}\pi}{\mathrm{10}}=\frac{\pi}{\mathrm{5}} \\ $$$$\left({r}+\frac{{r}}{\mathrm{sin}\:\alpha}\right)\mathrm{tan}\:\alpha=\frac{{a}}{\mathrm{2}} \\ $$$${r}=\frac{{a}\:\mathrm{cos}\:\alpha}{\mathrm{2}\left(\mathrm{1}+\mathrm{sin}\:\alpha\right)} \\ $$$${A}=\mathrm{10}\left[\frac{{r}^{\mathrm{2}} }{\mathrm{2}\:\mathrm{tan}\:\alpha}−\frac{{r}^{\mathrm{2}} }{\mathrm{2}}\left(\frac{\pi}{\mathrm{2}}−\alpha\right)\right] \\ $$$${A}=\mathrm{5}{r}^{\mathrm{2}} \left[\alpha+\frac{\mathrm{1}}{\mathrm{tan}\:\alpha}−\frac{\pi}{\mathrm{2}}\right] \\ $$$${A}=\frac{\mathrm{5}{a}^{\mathrm{2}} \mathrm{cos}^{\mathrm{2}} \:\alpha}{\mathrm{4}\left(\mathrm{1}+\mathrm{sin}\:\alpha\right)^{\mathrm{2}} }\left[\frac{\pi}{\mathrm{5}}+\frac{\mathrm{1}}{\mathrm{tan}\:\alpha}−\frac{\pi}{\mathrm{2}}\right] \\ $$$$\mathrm{cos}\:\alpha=\frac{\sqrt{\mathrm{5}}+\mathrm{1}}{\mathrm{4}} \\ $$$$\mathrm{sin}\:\alpha=\frac{\sqrt{\mathrm{2}\left(\mathrm{5}−\sqrt{\mathrm{5}}\right)}}{\mathrm{4}} \\ $$$$\mathrm{tan}\:\alpha=\sqrt{\mathrm{5}−\mathrm{2}\sqrt{\mathrm{5}}} \\ $$$${A}=\frac{{a}^{\mathrm{2}} \mathrm{cos}^{\mathrm{2}} \:\alpha}{\mathrm{8}\left(\mathrm{1}+\mathrm{sin}\:\alpha\right)^{\mathrm{2}} }\left[\frac{\mathrm{10}}{\mathrm{tan}\:\alpha}−\mathrm{3}\pi\right] \\ $$$${A}=\frac{{a}^{\mathrm{2}} \left(\sqrt{\mathrm{5}}+\mathrm{1}\right)^{\mathrm{2}} }{\mathrm{8}\left(\mathrm{4}+\sqrt{\mathrm{2}\left(\mathrm{5}−\sqrt{\mathrm{5}}\right.}\right)^{\mathrm{2}} }\left[\frac{\mathrm{10}\sqrt{\mathrm{5}+\mathrm{2}\sqrt{\mathrm{5}}}}{\:\sqrt{\mathrm{5}}}−\mathrm{3}\pi\right] \\ $$$$\Rightarrow{A}=\frac{\left.{a}^{\mathrm{2}} \left(\mathrm{3}+\sqrt{\mathrm{5}}\right)\left[\mathrm{2}\sqrt{\mathrm{5}\left(\mathrm{5}+\mathrm{2}\sqrt{\mathrm{5}}\right.}\right)−\mathrm{3}\pi\right]}{\mathrm{8}\left[\mathrm{13}−\sqrt{\mathrm{5}}+\mathrm{4}\sqrt{\mathrm{2}\left(\mathrm{5}−\sqrt{\mathrm{5}}\right)}\right]}\approx\mathrm{0}.\mathrm{14081}{a}^{\mathrm{2}} \\ $$
Commented by ajfour last updated on 23/Jan/19
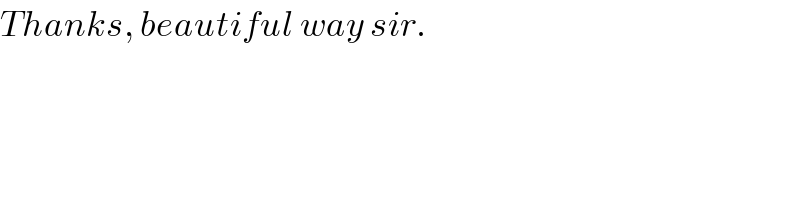
$${Thanks},\:{beautiful}\:{way}\:{sir}. \\ $$
Commented by mr W last updated on 23/Jan/19

$${thanks}\:{sir}! \\ $$
Commented by Otchere Abdullai last updated on 24/Jan/19

$${my}\:{prof} \\ $$
