Question Number 53676 by peter frank last updated on 24/Jan/19
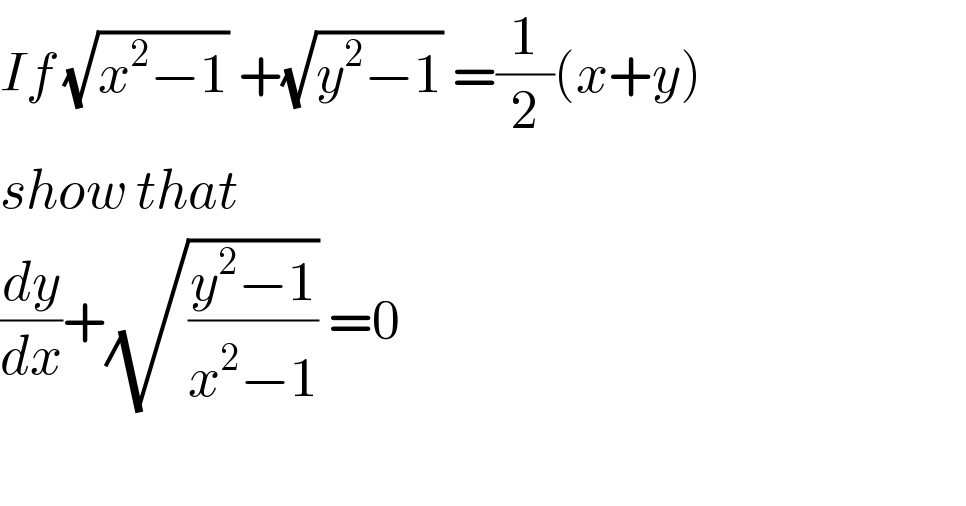
$${If}\:\sqrt{{x}^{\mathrm{2}} −\mathrm{1}}\:+\sqrt{{y}^{\mathrm{2}} −\mathrm{1}}\:=\frac{\mathrm{1}}{\mathrm{2}}\left({x}+{y}\right) \\ $$$${show}\:{that} \\ $$$$\frac{{dy}}{{dx}}+\sqrt{\frac{{y}^{\mathrm{2}} −\mathrm{1}}{{x}^{\mathrm{2}} −\mathrm{1}}}\:=\mathrm{0} \\ $$$$ \\ $$
Commented by math1967 last updated on 25/Jan/19
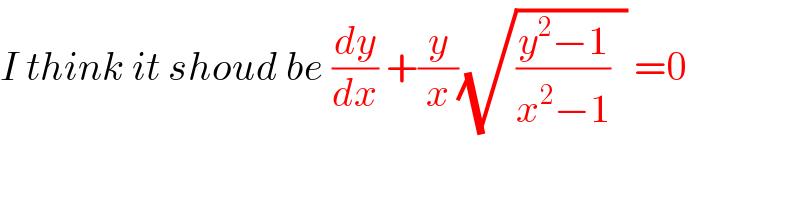
$${I}\:{think}\:{it}\:{shoud}\:{be}\:\frac{{dy}}{{dx}}\:+\frac{{y}}{{x}}\sqrt{\frac{{y}^{\mathrm{2}} −\mathrm{1}}{{x}^{\mathrm{2}} −\mathrm{1}}\:\:}\:=\mathrm{0} \\ $$
Commented by peter frank last updated on 25/Jan/19
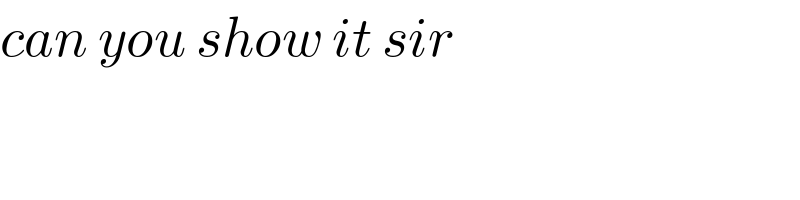
$${can}\:{you}\:{show}\:{it}\:{sir} \\ $$
Commented by math1967 last updated on 25/Jan/19

$${it}\:{is}\:{not}\:{true}\:{for}\:\frac{{dy}}{{dx}}\:+\frac{{y}}{{x}}\sqrt{\frac{{y}^{\mathrm{2}} −\mathrm{1}}{{x}^{\mathrm{2}} −\mathrm{1}}}=\mathrm{0} \\ $$$${it}\:{is}\:{my}\:{mistake} \\ $$
Commented by tanmay.chaudhury50@gmail.com last updated on 25/Jan/19
![let find true questin... 1)(dy/dx)+(√((y^2 −1)/(x^2 −1))) =0 (dy/( (√(y^2 −1))))+(dx/( (√(x^2 −1))))=0 ∫(dy/( (√(y^2 −1)) ))+∫(dx/( (√(x^2 −1)) ))=c ln(y+(√(y^2 −1)) )+ln(x+(√(x^2 −1))) =lnc (y+(√(y^2 −1)) )(x+(√(x^2 −1)) )=c 2)(dy/dx)+((y(√(y^2 −1)))/(x(√(x^2 −1))))=0 (dy/(y(√(y^2 −1))))+(dx/(x(√(x^2 −1))))=0 ∫(dy/(y(√(y^2 −1))))+∫(dx/(x(√(x^2 −1))))=c y=secθ_1 ∫((secθ_1 tanθ_1 dθ_1 )/(secθ_1 tanθ_1 ))+∫((secθ_2 tanθ_2 dθ_2 )/(secθ_2 tanθ_2 ))=c θ_1 +θ_2 =c sec^(−1) (y)+sec^(−1) (x)=c cos^(−1) ((1/y))+cos^(−1) ((1/x))=c cos[cos^(−1) ((1/y))+cos^(−1) ((1/x))]=cosc (1/y)×(1/x)−(√(1−(1/y^2 ))) ×(√(1−(1/x^2 ))) =cosc (1/(xy))−(((√(y^2 −1)) ×(√(x^2 −1)) )/(xy))=cosc 1−(√(y^2 −1)) ×(√(x^2 −1)) =xy×c_1 so pls recheck your auestion](https://www.tinkutara.com/question/Q53731.png)
$${let}\:{find}\:{true}\:{questin}… \\ $$$$\left.\mathrm{1}\right)\frac{{dy}}{{dx}}+\sqrt{\frac{{y}^{\mathrm{2}} −\mathrm{1}}{{x}^{\mathrm{2}} −\mathrm{1}}}\:=\mathrm{0} \\ $$$$\frac{{dy}}{\:\sqrt{{y}^{\mathrm{2}} −\mathrm{1}}}+\frac{{dx}}{\:\sqrt{{x}^{\mathrm{2}} −\mathrm{1}}}=\mathrm{0} \\ $$$$\int\frac{{dy}}{\:\sqrt{{y}^{\mathrm{2}} −\mathrm{1}}\:}+\int\frac{{dx}}{\:\sqrt{{x}^{\mathrm{2}} −\mathrm{1}}\:}={c} \\ $$$${ln}\left({y}+\sqrt{{y}^{\mathrm{2}} −\mathrm{1}}\:\right)+{ln}\left({x}+\sqrt{\left.{x}^{\mathrm{2}} −\mathrm{1}\right)}\:={lnc}\right. \\ $$$$\left({y}+\sqrt{{y}^{\mathrm{2}} −\mathrm{1}}\:\right)\left({x}+\sqrt{{x}^{\mathrm{2}} −\mathrm{1}}\:\right)={c} \\ $$$$ \\ $$$$\left.\mathrm{2}\right)\frac{{dy}}{{dx}}+\frac{{y}\sqrt{{y}^{\mathrm{2}} −\mathrm{1}}}{{x}\sqrt{{x}^{\mathrm{2}} −\mathrm{1}}}=\mathrm{0} \\ $$$$\frac{{dy}}{{y}\sqrt{{y}^{\mathrm{2}} −\mathrm{1}}}+\frac{{dx}}{{x}\sqrt{{x}^{\mathrm{2}} −\mathrm{1}}}=\mathrm{0} \\ $$$$\int\frac{{dy}}{{y}\sqrt{{y}^{\mathrm{2}} −\mathrm{1}}}+\int\frac{{dx}}{{x}\sqrt{{x}^{\mathrm{2}} −\mathrm{1}}}={c} \\ $$$${y}={sec}\theta_{\mathrm{1}} \\ $$$$\int\frac{{sec}\theta_{\mathrm{1}} {tan}\theta_{\mathrm{1}} {d}\theta_{\mathrm{1}} }{{sec}\theta_{\mathrm{1}} {tan}\theta_{\mathrm{1}} }+\int\frac{{sec}\theta_{\mathrm{2}} {tan}\theta_{\mathrm{2}} {d}\theta_{\mathrm{2}} }{{sec}\theta_{\mathrm{2}} {tan}\theta_{\mathrm{2}} }={c} \\ $$$$\theta_{\mathrm{1}} +\theta_{\mathrm{2}} ={c} \\ $$$${sec}^{−\mathrm{1}} \left({y}\right)+{sec}^{−\mathrm{1}} \left({x}\right)={c} \\ $$$${cos}^{−\mathrm{1}} \left(\frac{\mathrm{1}}{{y}}\right)+{cos}^{−\mathrm{1}} \left(\frac{\mathrm{1}}{{x}}\right)={c} \\ $$$${cos}\left[{cos}^{−\mathrm{1}} \left(\frac{\mathrm{1}}{{y}}\right)+{cos}^{−\mathrm{1}} \left(\frac{\mathrm{1}}{{x}}\right)\right]={cosc} \\ $$$$\frac{\mathrm{1}}{{y}}×\frac{\mathrm{1}}{{x}}−\sqrt{\mathrm{1}−\frac{\mathrm{1}}{{y}^{\mathrm{2}} }}\:×\sqrt{\mathrm{1}−\frac{\mathrm{1}}{{x}^{\mathrm{2}} }}\:={cosc} \\ $$$$\frac{\mathrm{1}}{{xy}}−\frac{\sqrt{{y}^{\mathrm{2}} −\mathrm{1}}\:×\sqrt{{x}^{\mathrm{2}} −\mathrm{1}}\:}{{xy}}={cosc} \\ $$$$\mathrm{1}−\sqrt{{y}^{\mathrm{2}} −\mathrm{1}}\:×\sqrt{{x}^{\mathrm{2}} −\mathrm{1}}\:={xy}×{c}_{\mathrm{1}} \\ $$$${so}\:{pls}\:{recheck}\:{your}\:{auestion} \\ $$$$ \\ $$
Commented by peter frank last updated on 25/Jan/19
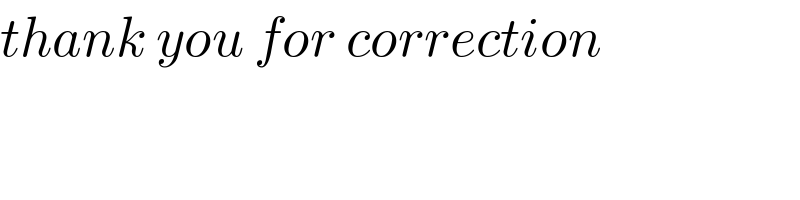
$${thank}\:{you}\:{for}\:{correction} \\ $$
