Menu Close

Question-119250

Tinku Tara 0 Comments
Pin




Question Number 119250 by Pengu last updated on 23/Oct/20
Commented by Pengu last updated on 23/Oct/20
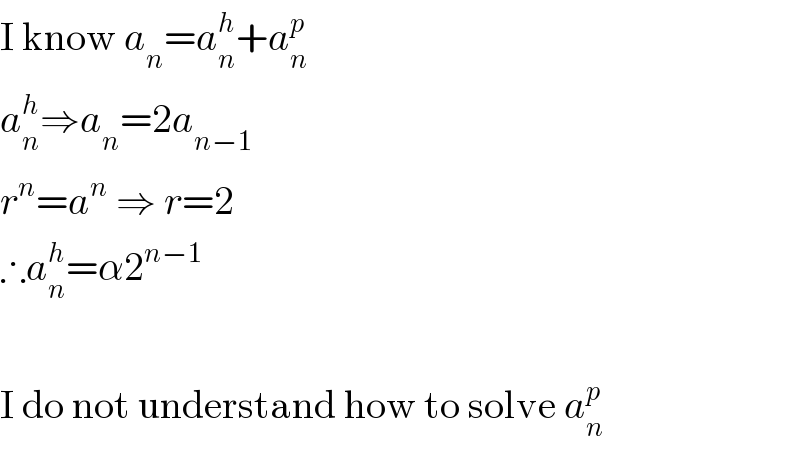
I know a_n =a_n ^h +a_n ^p a_n ^h ⇒a_n =2a_(n−1) r^n =a^n ⇒ r=2 ∴a_n ^h =α2^(n−1) I do not understand how to solve a_n ^p
$$\mathrm{I}\:\mathrm{know}\:{a}_{{n}} ={a}_{{n}} ^{{h}} +{a}_{{n}} ^{{p}} \\ $$$${a}_{{n}} ^{{h}} \Rightarrow{a}_{{n}} =\mathrm{2}{a}_{{n}−\mathrm{1}} \\ $$$${r}^{{n}} ={a}^{{n}} \:\Rightarrow\:{r}=\mathrm{2} \\ $$$$\therefore{a}_{{n}} ^{{h}} =\alpha\mathrm{2}^{{n}−\mathrm{1}} \\ $$$$\: \\ $$$$\mathrm{I}\:\mathrm{do}\:\mathrm{not}\:\mathrm{understand}\:\mathrm{how}\:\mathrm{to}\:\mathrm{solve}\:{a}_{{n}} ^{{p}} \\ $$
Commented by Pengu last updated on 23/Oct/20
Also, hello. I am not new. I am Filup, and have used this app for many years, but forgot my various account details. I wonder if anyone remembers me �� Filup, FilupErwinSmith, and Penguin have been my previous aliases. I am finally doing a mathematics degree, after many years.
Commented by mr W last updated on 23/Oct/20
welcome back sir! i still remember the discussion about the interesting question 12883 from you some years ago.
$${welcome}\:{back}\:{sir}! \\ $$$${i}\:{still}\:{remember}\:{the}\:{discussion}\:{about} \\ $$$${the}\:{interesting}\:{question}\:\mathrm{12883}\:{from} \\ $$$${you}\:{some}\:{years}\:{ago}. \\ $$
Commented by Pengu last updated on 23/Oct/20
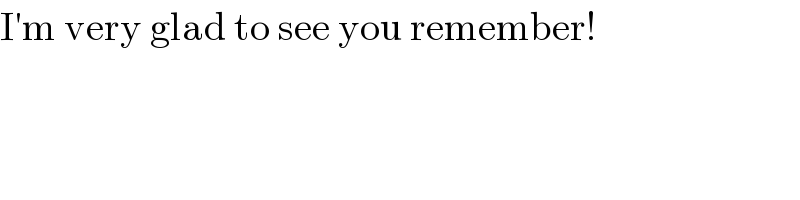
I′m very glad to see you remember!
$$\mathrm{I}'\mathrm{m}\:\mathrm{very}\:\mathrm{glad}\:\mathrm{to}\:\mathrm{see}\:\mathrm{you}\:\mathrm{remember}! \\ $$
Commented by prakash jain last updated on 24/Oct/20
Hi Filup, How are you?
Answered by 1549442205PVT last updated on 23/Oct/20
a)Given a_n =2a_(n−1) +2^n Consider solution a_n =n2^n ⇒a_(n−1) =(n−1)2^(n−1) ⇒2a_(n−1) =(n−1).2^n ⇒2a_(n−1) +2^n =n.2^n ⇒a_n =2a_(n−1) +2^n which shows that a_n =n2^n is a solution of the given concurrent relation b)Put a_n =2^n u_n ⇒a_(n+1) =2a_n +2^(n+1) ⇔2^(n+1) u_(n+1) =2.2^n u_n +2^(n+1) ⇒u_(n+1) =u_n +1⇒(u_n )is a A.P. with first term equal to u_0 =a_0 and common difference equal to 1.We infer u_n =a_0 +n⇒a_n =(a_0 +n)2^n .Thus, a_n =(n+a_0 )2^n is general term we need find c)For a_0 =2 we get a_n =(n+2)2^n
$$\left.\mathrm{a}\right)\mathrm{Given}\:\mathrm{a}_{\mathrm{n}} =\mathrm{2a}_{\mathrm{n}−\mathrm{1}} +\mathrm{2}^{\mathrm{n}} \\ $$$$\mathrm{Consider}\:\mathrm{solution}\:\mathrm{a}_{\mathrm{n}} =\mathrm{n2}^{\mathrm{n}} \Rightarrow\mathrm{a}_{\mathrm{n}−\mathrm{1}} =\left(\mathrm{n}−\mathrm{1}\right)\mathrm{2}^{\mathrm{n}−\mathrm{1}} \\ $$$$\Rightarrow\mathrm{2a}_{\mathrm{n}−\mathrm{1}} =\left(\mathrm{n}−\mathrm{1}\right).\mathrm{2}^{\mathrm{n}} \Rightarrow\mathrm{2a}_{\mathrm{n}−\mathrm{1}} +\mathrm{2}^{\mathrm{n}} =\mathrm{n}.\mathrm{2}^{\mathrm{n}} \\ $$$$\Rightarrow\mathrm{a}_{\mathrm{n}} =\mathrm{2a}_{\mathrm{n}−\mathrm{1}} +\mathrm{2}^{\mathrm{n}} \mathrm{which}\:\mathrm{shows}\:\mathrm{that} \\ $$$$\mathrm{a}_{\mathrm{n}} =\mathrm{n2}^{\mathrm{n}} \:\mathrm{is}\:\mathrm{a}\:\mathrm{solution}\:\mathrm{of}\:\mathrm{the}\:\mathrm{given}\:\mathrm{concurrent}\: \\ $$$$\mathrm{relation} \\ $$$$\left.\mathrm{b}\right)\mathrm{Put}\:\mathrm{a}_{\mathrm{n}} =\mathrm{2}^{\mathrm{n}} \mathrm{u}_{\mathrm{n}} \Rightarrow\mathrm{a}_{\mathrm{n}+\mathrm{1}} =\mathrm{2a}_{\mathrm{n}} +\mathrm{2}^{\mathrm{n}+\mathrm{1}} \\ $$$$\Leftrightarrow\mathrm{2}^{\mathrm{n}+\mathrm{1}} \mathrm{u}_{\mathrm{n}+\mathrm{1}} =\mathrm{2}.\mathrm{2}^{\mathrm{n}} \mathrm{u}_{\mathrm{n}} +\mathrm{2}^{\mathrm{n}+\mathrm{1}} \\ $$$$\Rightarrow\mathrm{u}_{\mathrm{n}+\mathrm{1}} =\mathrm{u}_{\mathrm{n}} +\mathrm{1}\Rightarrow\left(\mathrm{u}_{\mathrm{n}} \right)\mathrm{is}\:\mathrm{a}\:\mathrm{A}.\mathrm{P}.\:\mathrm{with} \\ $$$$\mathrm{first}\:\mathrm{term}\:\mathrm{equal}\:\mathrm{to}\:\mathrm{u}_{\mathrm{0}} =\mathrm{a}_{\mathrm{0}} \:\mathrm{and}\: \\ $$$$\mathrm{common}\:\mathrm{difference}\:\:\mathrm{equal}\:\mathrm{to}\:\mathrm{1}.\mathrm{We}\:\mathrm{infer} \\ $$$$\mathrm{u}_{\mathrm{n}} =\mathrm{a}_{\mathrm{0}} +\mathrm{n}\Rightarrow\mathrm{a}_{\mathrm{n}} =\left(\mathrm{a}_{\mathrm{0}} +\mathrm{n}\right)\mathrm{2}^{\mathrm{n}} .\mathrm{Thus}, \\ $$$$\mathrm{a}_{\mathrm{n}} =\left(\mathrm{n}+\mathrm{a}_{\mathrm{0}} \right)\mathrm{2}^{\mathrm{n}} \mathrm{is}\:\mathrm{general}\:\mathrm{term}\:\mathrm{we}\:\mathrm{need}\:\mathrm{find} \\ $$$$\left.\mathrm{c}\right)\mathrm{For}\:\mathrm{a}_{\mathrm{0}} =\mathrm{2}\:\mathrm{we}\:\mathrm{get}\:\mathrm{a}_{\mathrm{n}} =\left(\mathrm{n}+\mathrm{2}\right)\mathrm{2}^{\mathrm{n}} \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *