Question Number 119262 by bemath last updated on 23/Oct/20
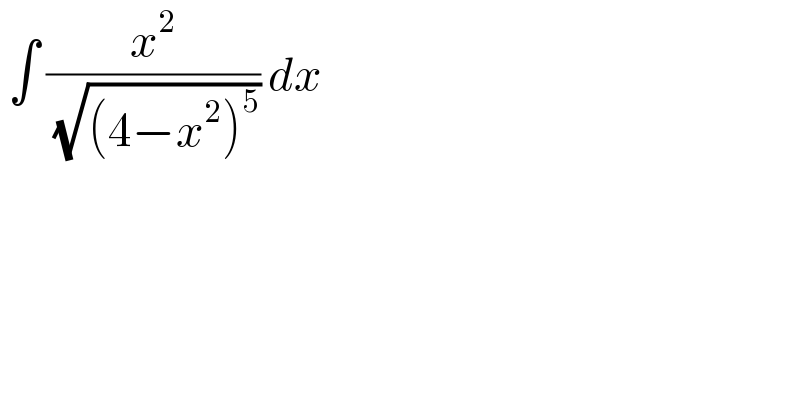
$$\:\int\:\frac{{x}^{\mathrm{2}} }{\:\sqrt{\left(\mathrm{4}−{x}^{\mathrm{2}} \right)^{\mathrm{5}} }}\:{dx}\: \\ $$
Answered by benjo_mathlover last updated on 23/Oct/20
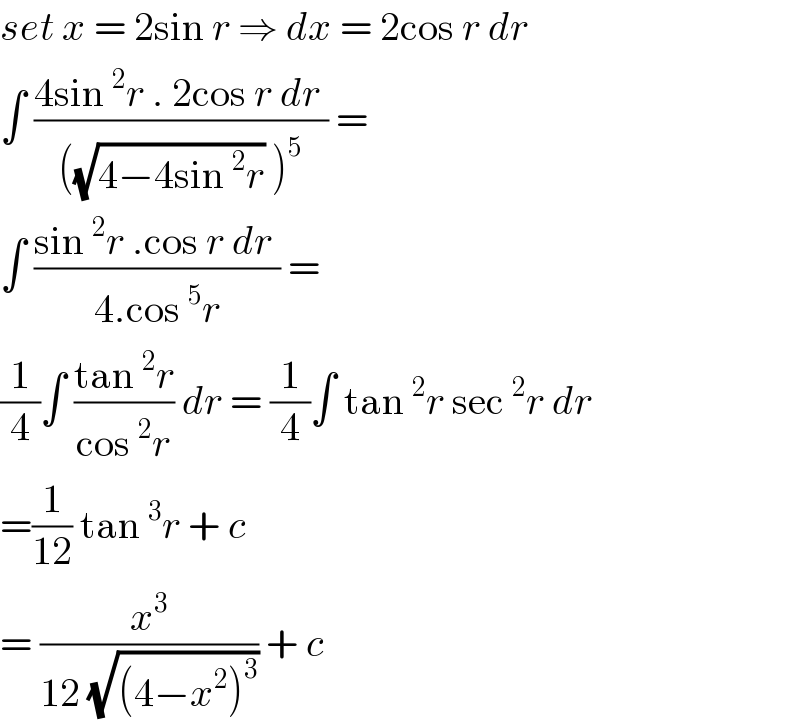
$${set}\:{x}\:=\:\mathrm{2sin}\:{r}\:\Rightarrow\:{dx}\:=\:\mathrm{2cos}\:{r}\:{dr}\: \\ $$$$\int\:\frac{\mathrm{4sin}\:^{\mathrm{2}} {r}\:.\:\mathrm{2cos}\:{r}\:{dr}\:}{\left(\sqrt{\mathrm{4}−\mathrm{4sin}\:^{\mathrm{2}} {r}}\:\right)^{\mathrm{5}} }\:= \\ $$$$\int\:\frac{\mathrm{sin}\:^{\mathrm{2}} {r}\:.\mathrm{cos}\:{r}\:{dr}\:}{\mathrm{4}.\mathrm{cos}\:^{\mathrm{5}} {r}}\:=\: \\ $$$$\frac{\mathrm{1}}{\mathrm{4}}\int\:\frac{\mathrm{tan}\:^{\mathrm{2}} {r}}{\mathrm{cos}\:^{\mathrm{2}} {r}}\:{dr}\:=\:\frac{\mathrm{1}}{\mathrm{4}}\int\:\mathrm{tan}\:^{\mathrm{2}} {r}\:\mathrm{sec}\:^{\mathrm{2}} {r}\:{dr} \\ $$$$=\frac{\mathrm{1}}{\mathrm{12}}\:\mathrm{tan}\:^{\mathrm{3}} {r}\:+\:{c}\: \\ $$$$=\:\frac{{x}^{\mathrm{3}} }{\mathrm{12}\:\sqrt{\left(\mathrm{4}−{x}^{\mathrm{2}} \right)^{\mathrm{3}} }}\:+\:{c} \\ $$
Answered by mathmax by abdo last updated on 23/Oct/20

$$\mathrm{I}=\int\:\:\frac{\mathrm{x}^{\mathrm{2}} }{\left(\mathrm{4}−\mathrm{x}^{\mathrm{2}} \right)^{\frac{\mathrm{5}}{\mathrm{2}}} }\mathrm{dx}\:\:\mathrm{we}\:\mathrm{do}\:\mathrm{the}\:\mathrm{changement}\:\mathrm{x}=\mathrm{2sint}\:\Rightarrow \\ $$$$\mathrm{I}\:=\int\:\:\frac{\mathrm{4sin}^{\mathrm{2}} \mathrm{t}}{\left(\mathrm{4cos}^{\mathrm{2}} \mathrm{t}\right)^{\frac{\mathrm{5}}{\mathrm{2}}} }\left(\mathrm{2cost}\right)\mathrm{dt}\:=\frac{\mathrm{8}}{\mathrm{4}^{\frac{\mathrm{5}}{\mathrm{2}}} }\int\:\:\frac{\mathrm{sin}^{\mathrm{2}} \mathrm{t}}{\mathrm{cos}^{\mathrm{4}} \mathrm{t}}\mathrm{dt}\:\:\mathrm{we}\:\mathrm{have} \\ $$$$\int\:\:\frac{\mathrm{sin}^{\mathrm{2}} \mathrm{t}}{\mathrm{cos}^{\mathrm{4}} \mathrm{t}}\:\mathrm{dt}\:=\int\:\frac{\mathrm{1}−\mathrm{cos}^{\mathrm{2}} \mathrm{t}}{\mathrm{cos}^{\mathrm{4}} \mathrm{t}}\mathrm{dt}\:=\int\:\frac{\mathrm{dt}}{\mathrm{cos}^{\mathrm{4}} \mathrm{t}}−\int\:\frac{\mathrm{dt}}{\mathrm{cos}^{\mathrm{2}} \mathrm{t}} \\ $$$$\int\:\:\frac{\mathrm{dt}}{\mathrm{cos}^{\mathrm{2}} \mathrm{t}}\:=\mathrm{tant}\:+\mathrm{c}_{\mathrm{1}} \:=\mathrm{tan}\left(\mathrm{arcsin}\left(\frac{\mathrm{x}}{\mathrm{2}}\right)\right)+\mathrm{c}_{\mathrm{1}} \\ $$$$\int\:\frac{\mathrm{dt}}{\mathrm{cos}^{\mathrm{4}} \mathrm{t}}\:=\int\:\:\frac{\mathrm{dt}}{\left(\frac{\mathrm{1}+\mathrm{cos}\left(\mathrm{2t}\right)}{\mathrm{2}}\right)^{\mathrm{2}} }\:=\int\:\:\frac{\mathrm{4dt}}{\mathrm{1}+\mathrm{2cos}\left(\mathrm{2t}\right)+\mathrm{cos}^{\mathrm{2}} \left(\mathrm{2t}\right)} \\ $$$$=\int\:\frac{\mathrm{4dt}}{\mathrm{1}+\mathrm{2cos}\left(\mathrm{2t}\right)+\frac{\mathrm{1}+\mathrm{cos}\left(\mathrm{4t}\right)}{\mathrm{2}}}\:=\int\:\frac{\mathrm{8dt}}{\mathrm{2}+\mathrm{4cos}\left(\mathrm{2t}\right)+\mathrm{1}+\mathrm{cos}\left(\mathrm{4t}\right)} \\ $$$$=\int\:\frac{\mathrm{8dt}}{\mathrm{3}+\mathrm{4cos}\left(\mathrm{2t}\right)+\mathrm{2cos}^{\mathrm{2}} \left(\mathrm{2t}\right)−\mathrm{1}}\:=_{\mathrm{2t}=\mathrm{u}} \:\:\:\:\int\:\:\frac{\mathrm{4du}}{\mathrm{2}+\mathrm{4cosu}+\mathrm{2cos}^{\mathrm{2}} \mathrm{u}} \\ $$$$=\mathrm{2}\int\:\:\frac{\mathrm{du}}{\mathrm{1}+\mathrm{2cosu}\:+\mathrm{cos}^{\mathrm{2}} \mathrm{u}}\:=\mathrm{2}\:\int\:\frac{\mathrm{du}}{\left(\mathrm{1}+\mathrm{cosu}\right)^{\mathrm{2}} }\:=_{\mathrm{tan}\left(\frac{\mathrm{u}}{\mathrm{2}}\right)=\mathrm{y}} \\ $$$$=\mathrm{2}\int\:\:\frac{\mathrm{2dy}}{\left(\mathrm{1}+\mathrm{y}^{\mathrm{2}} \right)\left(\mathrm{1}+\frac{\mathrm{1}−\mathrm{y}^{\mathrm{2}} }{\mathrm{1}+\mathrm{y}^{\mathrm{2}} }\right)^{\mathrm{2}} }\:=\mathrm{4}\int\:\frac{\mathrm{dy}}{\left(\mathrm{1}+\mathrm{y}^{\mathrm{2}} \right)×\frac{\mathrm{4}}{\left(\mathrm{1}+\mathrm{y}^{\mathrm{2}} \right)^{\mathrm{2}} }} \\ $$$$=\int\:\:\:\left(\mathrm{1}+\mathrm{y}^{\mathrm{2}} \right)\mathrm{dy}\:=\mathrm{y}+\frac{\mathrm{y}^{\mathrm{3}} }{\mathrm{3}}\:=\mathrm{tan}\left(\frac{\mathrm{u}}{\mathrm{2}}\right)+\frac{\mathrm{1}}{\mathrm{3}}\mathrm{tan}^{\mathrm{3}} \left(\frac{\mathrm{u}}{\mathrm{2}}\right)+\mathrm{c}_{\mathrm{2}} \\ $$$$=\mathrm{tan}\left(\mathrm{t}\right)+\frac{\mathrm{1}}{\mathrm{3}}\mathrm{tan}^{\mathrm{3}} \left(\mathrm{t}\right)+\mathrm{c}_{\mathrm{2}} \:=\mathrm{tan}\left(\mathrm{arcsn}\left(\frac{\mathrm{x}}{\mathrm{2}}\right)\right)+\frac{\mathrm{1}}{\mathrm{3}}\left(\mathrm{arcsin}\left(\frac{\mathrm{x}}{\mathrm{2}}\right)\right)^{\mathrm{3}} +\mathrm{c}_{\mathrm{2}} \\ $$$$\Rightarrow\mathrm{I}\:=\frac{\mathrm{2}^{\mathrm{3}} }{\mathrm{2}^{\mathrm{5}} }\left\{\mathrm{tan}\left(\mathrm{arcsin}\left(\frac{\mathrm{x}}{\mathrm{2}}\right)\right)+\frac{\mathrm{1}}{\mathrm{3}}\left(\mathrm{tanarcsin}\left(\frac{\mathrm{x}}{\mathrm{2}}\right)\right)^{\mathrm{3}} −\mathrm{tan}\left(\mathrm{arcsin}\left(\frac{\mathrm{x}}{\mathrm{2}}\right)\right)+\mathrm{C}\right. \\ $$$$=\frac{\mathrm{1}}{\mathrm{12}}\left(\mathrm{tan}\left(\mathrm{arcsin}\left(\frac{\mathrm{x}}{\mathrm{2}}\right)\right)^{\mathrm{3}} \right)\:+\mathrm{C} \\ $$
Answered by MJS_new last updated on 23/Oct/20
![without trigonometric substitution ∫(x^2 /((4−x^2 )^(5/2) ))dx= [t=(x/((4−x^2 )^(1/2) )) ⇔ x=((2t)/( (√(t^2 +1)))) → dx=(((4−x^2 )^(3/2) )/4)dt] =(1/4)∫t^2 dt=(1/(12))t^3 =(x^3 /(12(4−x^3 )^(3/2) ))+C](https://www.tinkutara.com/question/Q119284.png)
$$\mathrm{without}\:\mathrm{trigonometric}\:\mathrm{substitution} \\ $$$$\int\frac{{x}^{\mathrm{2}} }{\left(\mathrm{4}−{x}^{\mathrm{2}} \right)^{\mathrm{5}/\mathrm{2}} }{dx}= \\ $$$$\:\:\:\:\:\left[{t}=\frac{{x}}{\left(\mathrm{4}−{x}^{\mathrm{2}} \right)^{\mathrm{1}/\mathrm{2}} }\:\Leftrightarrow\:{x}=\frac{\mathrm{2}{t}}{\:\sqrt{{t}^{\mathrm{2}} +\mathrm{1}}}\:\rightarrow\:{dx}=\frac{\left(\mathrm{4}−{x}^{\mathrm{2}} \right)^{\mathrm{3}/\mathrm{2}} }{\mathrm{4}}{dt}\right] \\ $$$$=\frac{\mathrm{1}}{\mathrm{4}}\int{t}^{\mathrm{2}} {dt}=\frac{\mathrm{1}}{\mathrm{12}}{t}^{\mathrm{3}} =\frac{{x}^{\mathrm{3}} }{\mathrm{12}\left(\mathrm{4}−{x}^{\mathrm{3}} \right)^{\mathrm{3}/\mathrm{2}} }+{C} \\ $$
Commented by benjo_mathlover last updated on 23/Oct/20

$${amazing}…{sir} \\ $$$$ \\ $$
Commented by MJS_new last updated on 23/Oct/20

$$\mathrm{just}\:\mathrm{decades}\:\mathrm{of}\:\mathrm{experience} \\ $$
