Question Number 184938 by mnjuly1970 last updated on 14/Jan/23
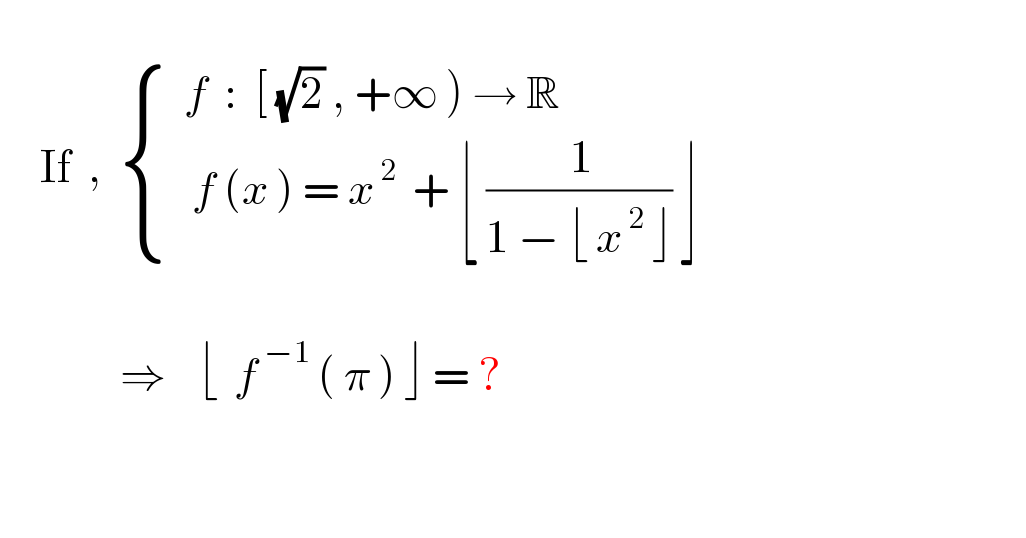
$$ \\ $$$$\:\:\:\:\:\mathrm{If}\:\:,\:\:\begin{cases}{\:\:{f}\:\::\:\:\left[\:\sqrt{\mathrm{2}}\:,\:+\infty\:\right)\:\rightarrow\:\mathbb{R}\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:}\\{\:\:\:{f}\:\left({x}\:\right)\:=\:{x}^{\:\mathrm{2}} \:\:+\:\lfloor\:\frac{\:\mathrm{1}}{\mathrm{1}\:−\:\lfloor\:{x}^{\:\mathrm{2}} \:\rfloor}\:\rfloor\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:}\end{cases} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\: \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\Rightarrow\:\:\:\:\lfloor\:\:{f}^{\:−\mathrm{1}} \:\left(\:\pi\:\right)\:\rfloor\:=\:? \\ $$$$ \\ $$$$ \\ $$
Answered by Frix last updated on 14/Jan/23

$$\sqrt{\pi+\mathrm{1}} \\ $$
Commented by mnjuly1970 last updated on 14/Jan/23

$${thanks}\:{alot}… \\ $$
Commented by Frix last updated on 14/Jan/23

$$\mathrm{Sorry}\:\mathrm{for}\:\mathrm{the}\:\mathrm{missing}\:\mathrm{solution},\:\mathrm{it}'\mathrm{s}\:\mathrm{just}\:\mathrm{the} \\ $$$$\mathrm{result}\:\mathrm{of}\:\mathrm{my}\:\mathrm{playing}\:\mathrm{around}\:\mathrm{with}\:\mathrm{it} \\ $$
Answered by mnjuly1970 last updated on 14/Jan/23

$$\:\:\:\:\:{my}\:{solution}\:: \\ $$$$\:\:\:\:{x}\geqslant\sqrt{\mathrm{2}}\:\Rightarrow\:{x}^{\:\mathrm{2}} \:\geqslant\:\mathrm{2}\:\Rightarrow\:\lfloor{x}\:^{\mathrm{2}} \:\rfloor\:\geqslant\:\mathrm{2} \\ $$$$\:\:\:\Rightarrow\:\:\:\mathrm{1}−\lfloor\:{x}^{\:\mathrm{2}} \:\rfloor\:\leqslant\:−\mathrm{1}<\mathrm{0} \\ $$$$\:\:\:\:\:\Rightarrow\:\mathrm{0}>\:\:\frac{\mathrm{1}}{\mathrm{1}−\lfloor{x}^{\:\mathrm{2}} \:\rfloor}\:\geqslant−\mathrm{1} \\ $$$$\:\:\:\:\:\:\:{f}\:\left({x}\right)=\:{x}^{\:\mathrm{2}} −\mathrm{1} \\ $$$$\:\:\:\:\:\:\:\:{f}^{\:−\mathrm{1}} \left({x}\right)\:=\sqrt{\:{x}+\mathrm{1}} \\ $$$$\:\:\:\:\:\:\:\:\lfloor\:{f}^{\:−\mathrm{1}} \left(\pi\:\right)\rfloor=\:\lfloor\:\sqrt{\pi+\mathrm{1}}\:\rfloor=\:\mathrm{2} \\ $$$$\:\:\:\: \\ $$
Commented by aba last updated on 14/Jan/23

$$\mathrm{good} \\ $$
Commented by Mastermind last updated on 15/Jan/23

$$\mathrm{Is}\:\mathrm{this}\:\mathrm{a}\:\mathrm{solution}\:\mathrm{to}\:\mathrm{my}\:\mathrm{question} \\ $$$$\mathrm{pls},\:\mathrm{could}\:\mathrm{you}\:\mathrm{please}\:\mathrm{make}\:\mathrm{it}\:\mathrm{easier} \\ $$$$\mathrm{than}\:\mathrm{this}? \\ $$
