Question Number 131507 by Chhing last updated on 05/Feb/21
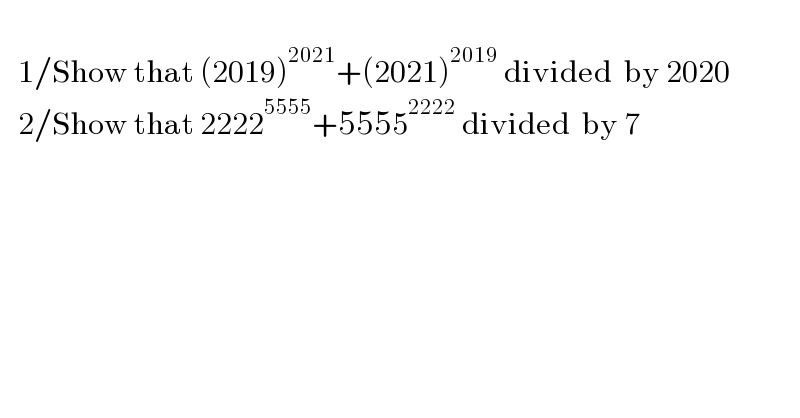
$$ \\ $$$$\:\:\:\mathrm{1}/\mathrm{Show}\:\mathrm{that}\:\left(\mathrm{2019}\right)^{\mathrm{2021}} +\left(\mathrm{2021}\right)^{\mathrm{2019}} \:\mathrm{divided}\:\:\mathrm{by}\:\mathrm{2020} \\ $$$$\:\:\:\mathrm{2}/\mathrm{Show}\:\mathrm{that}\:\mathrm{2222}^{\mathrm{5555}} +\mathrm{5555}^{\mathrm{2222}} \:\mathrm{divided}\:\:\mathrm{by}\:\mathrm{7} \\ $$$$ \\ $$
Answered by JDamian last updated on 05/Feb/21
![1/ (2019^(2021) +2021^(2019) )mod 2020= =[(2020−1)^(2021) +(2020+1)^(2019) ] mod 2020= =[(−1)^(2021) +1^(2019) ]mod 2020= =(−1+1)mod 2020=0](https://www.tinkutara.com/question/Q131511.png)
$$\mathrm{1}/ \\ $$$$\left(\mathrm{2019}^{\mathrm{2021}} +\mathrm{2021}^{\mathrm{2019}} \right){mod}\:\mathrm{2020}= \\ $$$$=\left[\left(\mathrm{2020}−\mathrm{1}\right)^{\mathrm{2021}} \:+\left(\mathrm{2020}+\mathrm{1}\right)^{\mathrm{2019}} \right]\:{mod}\:\mathrm{2020}= \\ $$$$=\left[\left(−\mathrm{1}\right)^{\mathrm{2021}} +\mathrm{1}^{\mathrm{2019}} \right]{mod}\:\mathrm{2020}= \\ $$$$=\left(−\mathrm{1}+\mathrm{1}\right){mod}\:\mathrm{2020}=\mathrm{0} \\ $$$$ \\ $$
