Question Number 53910 by ajfour last updated on 27/Jan/19

Commented by ajfour last updated on 27/Jan/19

$${Find}\:{maximum}\:{area}\:{of}\:{quadrilateral} \\ $$$${ABCD}. \\ $$
Commented by ajfour last updated on 27/Jan/19

Commented by ajfour last updated on 27/Jan/19

$${At}\:{least}\:{find}\:\theta\:{and}\:\phi\:{in}\:{terms}\:{of} \\ $$$${R}\:{and}\:{r}\:{such}\:{that}\:{area}\:{ABCDA}\:{is} \\ $$$${maximum}. \\ $$
Commented by ajfour last updated on 27/Jan/19
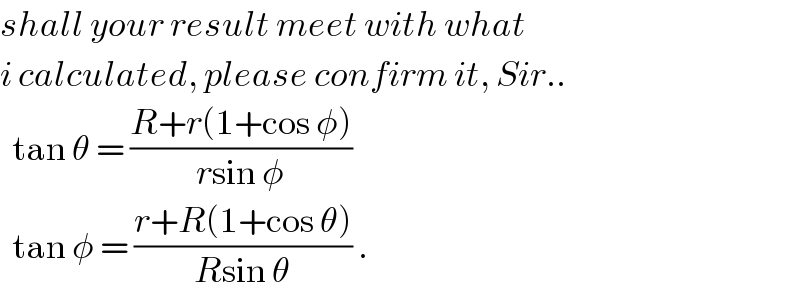
$${shall}\:{your}\:{result}\:{meet}\:{with}\:{what} \\ $$$${i}\:{calculated},\:{please}\:{confirm}\:{it},\:{Sir}.. \\ $$$$\:\:\mathrm{tan}\:\theta\:=\:\frac{{R}+{r}\left(\mathrm{1}+\mathrm{cos}\:\phi\right)}{{r}\mathrm{sin}\:\phi} \\ $$$$\:\:\mathrm{tan}\:\phi\:=\:\frac{{r}+{R}\left(\mathrm{1}+\mathrm{cos}\:\theta\right)}{{R}\mathrm{sin}\:\theta}\:. \\ $$
Commented by mr W last updated on 27/Jan/19

$${without}\:{calculation}\:{i}\:{guess}\:{the}\:{result} \\ $$$${is}\:{when}\:{tangent}\:{at}\:{D}\:{is}\:{parallel}\:{to} \\ $$$${diagonal}\:{AC}\:{and}\:{tangent}\:{at}\:{C}\:{is} \\ $$$${parallel}\:{to}\:{diagonal}\:{BD}.\: \\ $$$${i}.{e}.\:{CA}\bot{AD},\:{BD}\bot{BC}. \\ $$
Commented by ajfour last updated on 27/Jan/19

$${Brilliant}\:{professor}\:{Sir},\:{but}\:{my} \\ $$$${final}\:{cubic}\:{solution}\:{had}\:{error}, \\ $$$${i}\:{am}\:{trying}\:{to}\:{see}\:{if}\:{Cardano}'{s}\:{fit}, \\ $$$${please}\:{help}\:{there}. \\ $$
Commented by mr W last updated on 27/Jan/19

$${yes},\:{i}\:{can}\:{confirm}\:{that}\:{your}\:{solution} \\ $$$${matches}\:{that}\:{what}\:{i}\:{guess}. \\ $$
Commented by mr W last updated on 27/Jan/19

Commented by mr W last updated on 27/Jan/19
![∠BAC=(π/2)−θ [R+r(1+cos φ)]tan ((π/2)−θ)=r sin φ ⇒tan θ=((R+r(1+cos φ))/(r sin φ)) similarly: [r+R(1+cos θ)]tan ((π/2)−φ)=R sin θ ⇒tan φ=((r+R(1+cos θ))/(R sin θ))](https://www.tinkutara.com/question/Q53938.png)
$$\angle{BAC}=\frac{\pi}{\mathrm{2}}−\theta \\ $$$$\left[{R}+{r}\left(\mathrm{1}+\mathrm{cos}\:\phi\right)\right]\mathrm{tan}\:\left(\frac{\pi}{\mathrm{2}}−\theta\right)={r}\:\mathrm{sin}\:\phi \\ $$$$\Rightarrow\mathrm{tan}\:\theta=\frac{{R}+{r}\left(\mathrm{1}+\mathrm{cos}\:\phi\right)}{{r}\:\mathrm{sin}\:\phi} \\ $$$${similarly}: \\ $$$$\left[{r}+{R}\left(\mathrm{1}+\mathrm{cos}\:\theta\right)\right]\mathrm{tan}\:\left(\frac{\pi}{\mathrm{2}}−\phi\right)={R}\:\mathrm{sin}\:\theta \\ $$$$\Rightarrow\mathrm{tan}\:\phi=\frac{{r}+{R}\left(\mathrm{1}+\mathrm{cos}\:\theta\right)}{{R}\:\mathrm{sin}\:\theta} \\ $$
Commented by mr W last updated on 27/Jan/19

$${this}\:{is}\:{how}\:{i}\:{guess}\:{the}\:{result}: \\ $$$${if}\:{C}\:{is}\:{fixed}\:{on}\:{the}\:{second}\:{circle},\:{i}.{e}. \\ $$$$\Delta{ACB}\:{is}\:{fixed},\:{max}.\:\Delta{ACD}\:{is}\:{when} \\ $$$${tangent}\:{at}\:{D}\:{is}\:{parallel}\:{to}\:{AC},\:{for}\:{this} \\ $$$${is}\:{the}\:{max}.\:{altitude}\:{over}\:{AC}. \\ $$$${similarly}\:{if}\:{D}\:{is}\:{fixed}\:{on}\:{the}\:{first} \\ $$$${circle},\:{max}.\:\Delta{BDC}\:{is}\:{when}\:{tangent} \\ $$$${at}\:{C}\:{is}\:{parallel}\:{to}\:{BD}. \\ $$
Commented by mr W last updated on 27/Jan/19
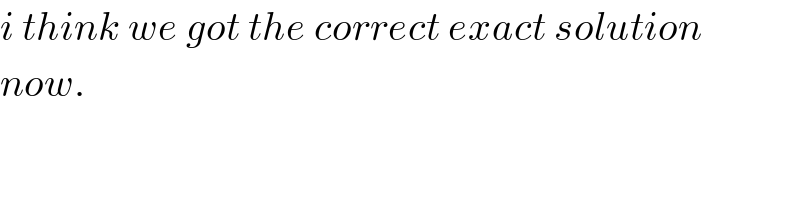
$${i}\:{think}\:{we}\:{got}\:{the}\:{correct}\:{exact}\:{solution} \\ $$$${now}. \\ $$
Commented by ajfour last updated on 28/Jan/19

$${I}\:{too}\:{believed}\:{Cardano}'{s}\:{method} \\ $$$${shall}\:{fetch}\:{all}\:{roots},\:{whether}\:{real} \\ $$$${or}\:{complex};\:{MjS}\:{sir}'{s}\:{comment} \\ $$$${once}\:{had}\:{let}\:{me}\:{doubt}\:{this}\:{belief} \\ $$$${for}\:{some}\:{time};\:{or}\:{may}\:{be}\:{i} \\ $$$${misinterpreted}\:{it}..{thanks}! \\ $$
Answered by ajfour last updated on 27/Jan/19

Commented by ajfour last updated on 27/Jan/19
![C(R+r+rcos φ, rsin φ) A=Area(△ABC)+Area(△ACD) A=(((R+r)/2))rsin φ+((Rh)/2) Eq. of AD: y=−xtan θ h=[rsin φ+(R+r+rcos φ)tan θ]cos θ =rsin φcos θ+(R+r+rcos φ)sin θ = (R+r)sin θ+rsin (θ+φ) 2A=(R+r)rsin φ+R(R+r)sin θ +Rrsin (θ+φ) let μ=(R/r) ⇒ 2A/r^2 =(μ+1)sin φ+μ(1+μ)sin θ +μsin (θ+φ) ((2A)/((μ+1)r^2 ))=sin φ+μsin θ+λsin (θ+φ) where λ=(μ/(μ+1)) =(R/(R+r)) ((2/((μ+1)r^2 )))((∂(A))/∂θ)=μcos θ+λcos (θ+φ)=0 ⇒ μcos θ = −λcos (θ+φ) ...(i) ((2/((μ+1)r^2 )))((∂(A))/∂φ)= cos φ+λcos (θ+φ)=0 ⇒ cos φ = −λcos (θ+φ) ...(ii) ⇒ cos φ = μcos θ Now using (i) with μ/λ = b=μ+1 bcos θ+cos θcos φ−sin θsin φ=0 cos^2 θ(b+μcos θ)^2 =(1−cos^2 θ)(1−μ^2 cos^2 θ) let cos θ= z ⇒ b^2 z^2 +2μbz^3 =1−μ^2 z^2 −z^2 but b=μ+1 , ⇒ 2(μ^2 +μ+1)z^2 +2μ(μ+1)z^3 −1=0 ⇒ (1/z^3 )−2(μ^2 +μ+1)(1/z)−2μ(μ+1)=0 (1/z)=(1/(cos θ))=sec θ = t ⇒ t^3 +pt+q =0 with p=−2(μ^2 +μ+1) ; q=−2μ(μ+1) (q^2 /4)+(p^3 /(27)) = μ^2 (μ+1)^2 −((8(μ^2 +μ+1)^3 )/(27)) D < 0 perhaps (as μ>1) ....](https://www.tinkutara.com/question/Q53940.png)
$${C}\left({R}+{r}+{r}\mathrm{cos}\:\phi,\:{r}\mathrm{sin}\:\phi\right) \\ $$$${A}={Area}\left(\bigtriangleup{ABC}\right)+{Area}\left(\bigtriangleup{ACD}\right) \\ $$$${A}=\left(\frac{{R}+{r}}{\mathrm{2}}\right){r}\mathrm{sin}\:\phi+\frac{{Rh}}{\mathrm{2}} \\ $$$${Eq}.\:{of}\:{AD}:\:\:\:{y}=−{x}\mathrm{tan}\:\theta \\ $$$$\:{h}=\left[{r}\mathrm{sin}\:\phi+\left({R}+{r}+{r}\mathrm{cos}\:\phi\right)\mathrm{tan}\:\theta\right]\mathrm{cos}\:\theta \\ $$$$\:\:={r}\mathrm{sin}\:\phi\mathrm{cos}\:\theta+\left({R}+{r}+{r}\mathrm{cos}\:\phi\right)\mathrm{sin}\:\theta \\ $$$$\:\:=\:\left({R}+{r}\right)\mathrm{sin}\:\theta+{r}\mathrm{sin}\:\left(\theta+\phi\right) \\ $$$$\mathrm{2}{A}=\left({R}+{r}\right){r}\mathrm{sin}\:\phi+{R}\left({R}+{r}\right)\mathrm{sin}\:\theta \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:+{Rr}\mathrm{sin}\:\left(\theta+\phi\right) \\ $$$${let}\:\:\mu=\frac{{R}}{{r}}\: \\ $$$$\Rightarrow\:\mathrm{2}{A}/{r}^{\mathrm{2}} =\left(\mu+\mathrm{1}\right)\mathrm{sin}\:\phi+\mu\left(\mathrm{1}+\mu\right)\mathrm{sin}\:\theta \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:+\mu\mathrm{sin}\:\left(\theta+\phi\right) \\ $$$$\frac{\mathrm{2}{A}}{\left(\mu+\mathrm{1}\right){r}^{\mathrm{2}} }=\mathrm{sin}\:\phi+\mu\mathrm{sin}\:\theta+\lambda\mathrm{sin}\:\left(\theta+\phi\right) \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:{where}\:\lambda=\frac{\mu}{\mu+\mathrm{1}}\:=\frac{{R}}{{R}+{r}} \\ $$$$\left(\frac{\mathrm{2}}{\left(\mu+\mathrm{1}\right){r}^{\mathrm{2}} }\right)\frac{\partial\left({A}\right)}{\partial\theta}=\mu\mathrm{cos}\:\theta+\lambda\mathrm{cos}\:\left(\theta+\phi\right)=\mathrm{0} \\ $$$$\Rightarrow\:\:\mu\mathrm{cos}\:\theta\:=\:−\lambda\mathrm{cos}\:\left(\theta+\phi\right)\:\:\:\:…\left({i}\right) \\ $$$$\left(\frac{\mathrm{2}}{\left(\mu+\mathrm{1}\right){r}^{\mathrm{2}} }\right)\frac{\partial\left({A}\right)}{\partial\phi}=\:\mathrm{cos}\:\phi+\lambda\mathrm{cos}\:\left(\theta+\phi\right)=\mathrm{0} \\ $$$$\Rightarrow\:\:\mathrm{cos}\:\phi\:=\:−\lambda\mathrm{cos}\:\left(\theta+\phi\right)\:\:\:\:\:…\left({ii}\right) \\ $$$$\Rightarrow\:\:\:\:\mathrm{cos}\:\phi\:=\:\mu\mathrm{cos}\:\theta \\ $$$$\:\:\:\:{Now}\:{using}\:\left({i}\right)\:{with}\:\mu/\lambda\:=\:{b}=\mu+\mathrm{1} \\ $$$$\:\:\:{b}\mathrm{cos}\:\theta+\mathrm{cos}\:\theta\mathrm{cos}\:\phi−\mathrm{sin}\:\theta\mathrm{sin}\:\phi=\mathrm{0} \\ $$$$\mathrm{cos}\:^{\mathrm{2}} \theta\left({b}+\mu\mathrm{cos}\:\theta\right)^{\mathrm{2}} =\left(\mathrm{1}−\mathrm{cos}\:^{\mathrm{2}} \theta\right)\left(\mathrm{1}−\mu^{\mathrm{2}} \mathrm{cos}\:^{\mathrm{2}} \theta\right) \\ $$$${let}\:\:\mathrm{cos}\:\theta=\:{z} \\ $$$$\Rightarrow\:{b}^{\mathrm{2}} {z}^{\mathrm{2}} +\mathrm{2}\mu{bz}^{\mathrm{3}} =\mathrm{1}−\mu^{\mathrm{2}} {z}^{\mathrm{2}} −{z}^{\mathrm{2}} \\ $$$${but}\:{b}=\mu+\mathrm{1}\:,\:\Rightarrow \\ $$$$\:\:\:\:\:\mathrm{2}\left(\mu^{\mathrm{2}} +\mu+\mathrm{1}\right){z}^{\mathrm{2}} +\mathrm{2}\mu\left(\mu+\mathrm{1}\right){z}^{\mathrm{3}} −\mathrm{1}=\mathrm{0} \\ $$$$\Rightarrow\:\:\frac{\mathrm{1}}{{z}^{\mathrm{3}} }−\mathrm{2}\left(\mu^{\mathrm{2}} +\mu+\mathrm{1}\right)\frac{\mathrm{1}}{{z}}−\mathrm{2}\mu\left(\mu+\mathrm{1}\right)=\mathrm{0} \\ $$$$\frac{\mathrm{1}}{{z}}=\frac{\mathrm{1}}{\mathrm{cos}\:\theta}=\mathrm{sec}\:\theta\:=\:{t} \\ $$$$\Rightarrow\:\boldsymbol{{t}}^{\mathrm{3}} +\boldsymbol{{pt}}+\boldsymbol{{q}}\:=\mathrm{0} \\ $$$${with}\:\:{p}=−\mathrm{2}\left(\mu^{\mathrm{2}} +\mu+\mathrm{1}\right)\:;\:{q}=−\mathrm{2}\mu\left(\mu+\mathrm{1}\right) \\ $$$$\frac{{q}^{\mathrm{2}} }{\mathrm{4}}+\frac{{p}^{\mathrm{3}} }{\mathrm{27}}\:=\:\mu^{\mathrm{2}} \left(\mu+\mathrm{1}\right)^{\mathrm{2}} −\frac{\mathrm{8}\left(\mu^{\mathrm{2}} +\mu+\mathrm{1}\right)^{\mathrm{3}} }{\mathrm{27}} \\ $$$$\:{D}\:<\:\mathrm{0}\:{perhaps}\:\left({as}\:\mu>\mathrm{1}\right) \\ $$$$…. \\ $$
Commented by ajfour last updated on 27/Jan/19

$${Thanks}\:{a}\:{lot}\:{Sir}! \\ $$
Commented by mr W last updated on 27/Jan/19

Commented by mr W last updated on 28/Jan/19
![t^3 −pt−q =0 with p=2(μ^2 +μ+1) ; q=2μ(μ+1) (u+v)^3 −3uv(u+v)−(u^3 +v^3 )=0 let t=u+v u^3 v^3 =((p/3))^3 =(8/(27))(μ^2 +μ+1)^3 u^3 +v^3 =q=2μ(μ+1) u^3 and v^3 are roots of x^2 −2μ(μ+1)x+(8/(27))(μ^2 +μ+1)^3 =0 D=4[μ^2 (μ+1)^2 −(8/(27))(μ^2 +μ+1)^3 ]<0 u^3 (v^3 )=μ(μ+1)±i(√((8/(27))(μ^2 +μ+1)^3 −μ^2 (μ+1)^2 ))=A±iB with A=μ(μ+1), B=(√((8/(27))(μ^2 +μ+1)^3 −μ^2 (μ+1)^2 )) A+iB=(√(A^2 +B^2 ))((A/( (√(A^2 +B^2 ))))+i(B/( (√(A^2 +B^2 )))))=(√(A^2 +B^2 ))(cos α+i sin α) with α=tan^(−1) (B/A)=tan^(−1) (√(((8(μ^2 +μ+1)^3 )/(27μ^2 (μ+1)^2 ))−1)) A^2 +B^2 =(8/(27))(μ^2 +μ+1)^3 u^3 (v^3 )=(√(A^2 +B^2 ))(cos α±i sin α) ⇒u=((A^2 +B^2 ))^(1/6) [cos (((α+2nπ)/3))+i sin (((α+2nπ)/3))] ⇒v=((A^2 +B^2 ))^(1/6) [cos (((α+2nπ)/3))−i sin (((α+2nπ)/3))] ⇒t=u+v=2((A^2 +B^2 ))^(1/6) cos (((α+2nπ)/3)), n=0,1,2 ⇒t=sec θ=2(√((2(μ^2 +μ+1))/3)) cos ((1/3)tan^(−1) (√(((8(μ^2 +μ+1)^3 )/(27μ^2 (μ+1)^2 ))−1)))](https://www.tinkutara.com/question/Q53975.png)
$$\:\boldsymbol{{t}}^{\mathrm{3}} −\boldsymbol{{pt}}−\boldsymbol{{q}}\:=\mathrm{0} \\ $$$${with}\:\:{p}=\mathrm{2}\left(\mu^{\mathrm{2}} +\mu+\mathrm{1}\right)\:;\:{q}=\mathrm{2}\mu\left(\mu+\mathrm{1}\right) \\ $$$$\left({u}+{v}\right)^{\mathrm{3}} −\mathrm{3}{uv}\left({u}+{v}\right)−\left({u}^{\mathrm{3}} +{v}^{\mathrm{3}} \right)=\mathrm{0} \\ $$$${let}\:{t}={u}+{v} \\ $$$${u}^{\mathrm{3}} {v}^{\mathrm{3}} =\left(\frac{{p}}{\mathrm{3}}\right)^{\mathrm{3}} =\frac{\mathrm{8}}{\mathrm{27}}\left(\mu^{\mathrm{2}} +\mu+\mathrm{1}\right)^{\mathrm{3}} \\ $$$${u}^{\mathrm{3}} +{v}^{\mathrm{3}} ={q}=\mathrm{2}\mu\left(\mu+\mathrm{1}\right) \\ $$$${u}^{\mathrm{3}} \:{and}\:{v}^{\mathrm{3}} \:{are}\:{roots}\:{of}\: \\ $$$${x}^{\mathrm{2}} −\mathrm{2}\mu\left(\mu+\mathrm{1}\right){x}+\frac{\mathrm{8}}{\mathrm{27}}\left(\mu^{\mathrm{2}} +\mu+\mathrm{1}\right)^{\mathrm{3}} =\mathrm{0} \\ $$$${D}=\mathrm{4}\left[\mu^{\mathrm{2}} \left(\mu+\mathrm{1}\right)^{\mathrm{2}} −\frac{\mathrm{8}}{\mathrm{27}}\left(\mu^{\mathrm{2}} +\mu+\mathrm{1}\right)^{\mathrm{3}} \right]<\mathrm{0} \\ $$$${u}^{\mathrm{3}} \left({v}^{\mathrm{3}} \right)=\mu\left(\mu+\mathrm{1}\right)\pm{i}\sqrt{\frac{\mathrm{8}}{\mathrm{27}}\left(\mu^{\mathrm{2}} +\mu+\mathrm{1}\right)^{\mathrm{3}} −\mu^{\mathrm{2}} \left(\mu+\mathrm{1}\right)^{\mathrm{2}} }={A}\pm{iB} \\ $$$${with}\:{A}=\mu\left(\mu+\mathrm{1}\right),\:{B}=\sqrt{\frac{\mathrm{8}}{\mathrm{27}}\left(\mu^{\mathrm{2}} +\mu+\mathrm{1}\right)^{\mathrm{3}} −\mu^{\mathrm{2}} \left(\mu+\mathrm{1}\right)^{\mathrm{2}} } \\ $$$${A}+{iB}=\sqrt{{A}^{\mathrm{2}} +{B}^{\mathrm{2}} }\left(\frac{{A}}{\:\sqrt{{A}^{\mathrm{2}} +{B}^{\mathrm{2}} }}+{i}\frac{{B}}{\:\sqrt{{A}^{\mathrm{2}} +{B}^{\mathrm{2}} }}\right)=\sqrt{{A}^{\mathrm{2}} +{B}^{\mathrm{2}} }\left(\mathrm{cos}\:\alpha+{i}\:\mathrm{sin}\:\alpha\right) \\ $$$${with}\:\alpha=\mathrm{tan}^{−\mathrm{1}} \frac{{B}}{{A}}=\mathrm{tan}^{−\mathrm{1}} \sqrt{\frac{\mathrm{8}\left(\mu^{\mathrm{2}} +\mu+\mathrm{1}\right)^{\mathrm{3}} }{\mathrm{27}\mu^{\mathrm{2}} \left(\mu+\mathrm{1}\right)^{\mathrm{2}} }−\mathrm{1}} \\ $$$${A}^{\mathrm{2}} +{B}^{\mathrm{2}} =\frac{\mathrm{8}}{\mathrm{27}}\left(\mu^{\mathrm{2}} +\mu+\mathrm{1}\right)^{\mathrm{3}} \\ $$$${u}^{\mathrm{3}} \left({v}^{\mathrm{3}} \right)=\sqrt{{A}^{\mathrm{2}} +{B}^{\mathrm{2}} }\left(\mathrm{cos}\:\alpha\pm{i}\:\mathrm{sin}\:\alpha\right) \\ $$$$\Rightarrow{u}=\sqrt[{\mathrm{6}}]{{A}^{\mathrm{2}} +{B}^{\mathrm{2}} }\left[\mathrm{cos}\:\left(\frac{\alpha+\mathrm{2}{n}\pi}{\mathrm{3}}\right)+{i}\:\mathrm{sin}\:\left(\frac{\alpha+\mathrm{2}{n}\pi}{\mathrm{3}}\right)\right] \\ $$$$\Rightarrow{v}=\sqrt[{\mathrm{6}}]{{A}^{\mathrm{2}} +{B}^{\mathrm{2}} }\left[\mathrm{cos}\:\left(\frac{\alpha+\mathrm{2}{n}\pi}{\mathrm{3}}\right)−{i}\:\mathrm{sin}\:\left(\frac{\alpha+\mathrm{2}{n}\pi}{\mathrm{3}}\right)\right] \\ $$$$\Rightarrow{t}={u}+{v}=\mathrm{2}\sqrt[{\mathrm{6}}]{{A}^{\mathrm{2}} +{B}^{\mathrm{2}} }\:\mathrm{cos}\:\left(\frac{\alpha+\mathrm{2}{n}\pi}{\mathrm{3}}\right),\:{n}=\mathrm{0},\mathrm{1},\mathrm{2} \\ $$$$\Rightarrow{t}=\mathrm{sec}\:\theta=\mathrm{2}\sqrt{\frac{\mathrm{2}\left(\mu^{\mathrm{2}} +\mu+\mathrm{1}\right)}{\mathrm{3}}}\:\mathrm{cos}\:\left(\frac{\mathrm{1}}{\mathrm{3}}\mathrm{tan}^{−\mathrm{1}} \sqrt{\frac{\mathrm{8}\left(\mu^{\mathrm{2}} +\mu+\mathrm{1}\right)^{\mathrm{3}} }{\mathrm{27}\mu^{\mathrm{2}} \left(\mu+\mathrm{1}\right)^{\mathrm{2}} }−\mathrm{1}}\right) \\ $$
Commented by ajfour last updated on 27/Jan/19

$$\mathcal{EXCELLENT}\:\:\:{Sir},\:{but}\:\:{wont}\:{any}\:{of} \\ $$$${the}\:{other}\:{two}\:{solutions}\:{might}\:{fit}? \\ $$
Commented by mr W last updated on 27/Jan/19

$${no},\:{because}\:{we}\:{expect}\:{that}\:\mathrm{0}<\theta<\frac{\pi}{\mathrm{2}}. \\ $$
Commented by mr W last updated on 27/Jan/19

$${example}: \\ $$$$\mu=\frac{{R}}{{r}}=\mathrm{1},\:\theta=\phi=\mathrm{68}.\mathrm{53}° \\ $$$${check}: \\ $$$${from}\:\mathrm{tan}\:\theta=\frac{{R}+{r}\left(\mathrm{1}+\mathrm{cos}\:\phi\right)}{{r}\:\mathrm{sin}\:\phi} \\ $$$$\Rightarrow\mathrm{tan}\:\theta=\frac{\mathrm{2}+\mathrm{cos}\:\theta}{\mathrm{sin}\:\theta} \\ $$$$\mathrm{2cos}^{\mathrm{2}} \:\theta+\mathrm{2cos}\:\theta−\mathrm{1}=\mathrm{0} \\ $$$$\mathrm{cos}\:\theta=\frac{\sqrt{\mathrm{3}}−\mathrm{1}}{\mathrm{2}} \\ $$$$\Rightarrow\theta=\mathrm{cos}^{−\mathrm{1}} \frac{\sqrt{\mathrm{3}}−\mathrm{1}}{\mathrm{2}}=\mathrm{68}.\mathrm{53}°\: \\ $$
