Question Number 136381 by mnjuly1970 last updated on 21/Mar/21
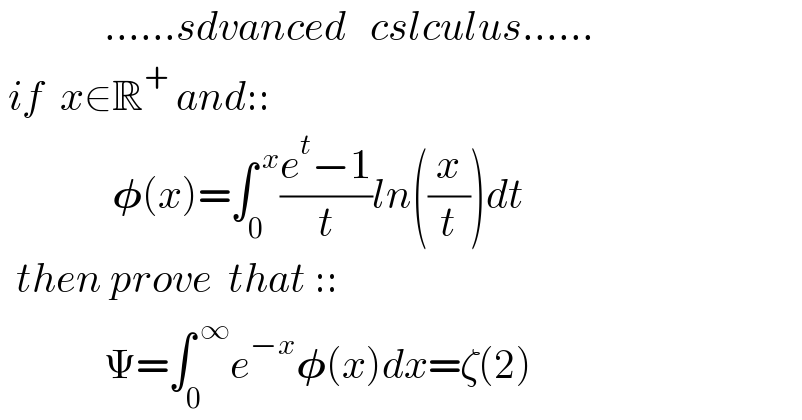
$$\:\:\:\:\:\:\:\:\:\:\:\:\:……{sdvanced}\:\:\:{cslculus}…… \\ $$$$\:{if}\:\:{x}\in\mathbb{R}^{+} \:{and}::\: \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\boldsymbol{\phi}\left({x}\right)=\int_{\mathrm{0}} ^{\:{x}} \frac{{e}^{{t}} −\mathrm{1}}{{t}}{ln}\left(\frac{{x}}{{t}}\right){dt} \\ $$$$\:\:{then}\:{prove}\:\:{that}\::: \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\Psi=\int_{\mathrm{0}} ^{\:\infty} {e}^{−{x}} \boldsymbol{\phi}\left({x}\right){dx}=\zeta\left(\mathrm{2}\right) \\ $$
Answered by Ñï= last updated on 21/Mar/21
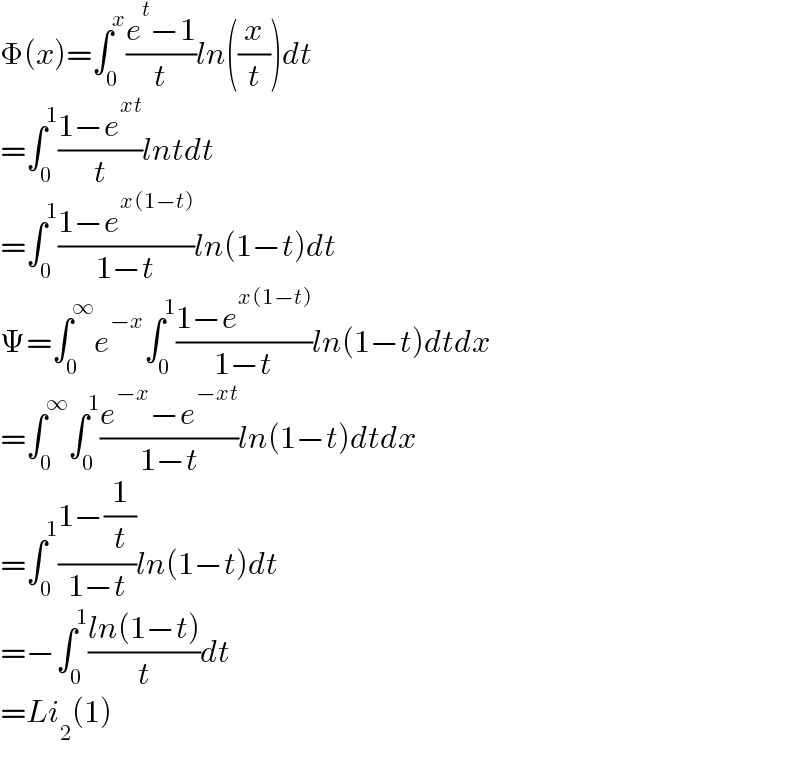
$$\Phi\left({x}\right)=\int_{\mathrm{0}} ^{{x}} \frac{{e}^{{t}} −\mathrm{1}}{{t}}{ln}\left(\frac{{x}}{{t}}\right){dt} \\ $$$$=\int_{\mathrm{0}} ^{\mathrm{1}} \frac{\mathrm{1}−{e}^{{xt}} }{{t}}{lntdt} \\ $$$$=\int_{\mathrm{0}} ^{\mathrm{1}} \frac{\mathrm{1}−{e}^{{x}\left(\mathrm{1}−{t}\right)} }{\mathrm{1}−{t}}{ln}\left(\mathrm{1}−{t}\right){dt} \\ $$$$\Psi=\int_{\mathrm{0}} ^{\infty} {e}^{−{x}} \int_{\mathrm{0}} ^{\mathrm{1}} \frac{\mathrm{1}−{e}^{{x}\left(\mathrm{1}−{t}\right)} }{\mathrm{1}−{t}}{ln}\left(\mathrm{1}−{t}\right){dtdx} \\ $$$$=\int_{\mathrm{0}} ^{\infty} \int_{\mathrm{0}} ^{\mathrm{1}} \frac{{e}^{−{x}} −{e}^{−{xt}} }{\mathrm{1}−{t}}{ln}\left(\mathrm{1}−{t}\right){dtdx} \\ $$$$=\int_{\mathrm{0}} ^{\mathrm{1}} \frac{\mathrm{1}−\frac{\mathrm{1}}{{t}}}{\mathrm{1}−{t}}{ln}\left(\mathrm{1}−{t}\right){dt} \\ $$$$=−\int_{\mathrm{0}} ^{\mathrm{1}} \frac{{ln}\left(\mathrm{1}−{t}\right)}{{t}}{dt} \\ $$$$={Li}_{\mathrm{2}} \left(\mathrm{1}\right) \\ $$
Commented by mnjuly1970 last updated on 21/Mar/21
$${thank}\:{you}\:{sir}…{grateful}.. \\ $$
