Question Number 5319 by Rasheed Soomro last updated on 07/May/16

$$\mathrm{A}\:\boldsymbol{\mathrm{sphere}}\:\mathrm{of}\:\mathrm{radius}\:\boldsymbol{\mathrm{r}}\:\mathrm{contains}\:\mathrm{a}\:\boldsymbol{\mathrm{cube}} \\ $$$$\mathrm{inside}\:\mathrm{it}.\:\mathrm{All}\:\mathrm{the}\:\boldsymbol{\mathrm{vertices}}\:\mathrm{of}\:\mathrm{the}\:\mathrm{cube} \\ $$$$\mathrm{touch}\:\mathrm{the}\:\boldsymbol{\mathrm{surface}}\:\mathrm{of}\:\mathrm{sphere}. \\ $$$$\mathrm{What}\:\mathrm{is}\:\mathrm{the}\:\boldsymbol{\mathrm{volume}}\:\mathrm{of}\:\mathrm{the}\:\mathrm{cube}? \\ $$
Answered by Rasheed Soomro last updated on 08/May/16

Commented by Rasheed Soomro last updated on 08/May/16
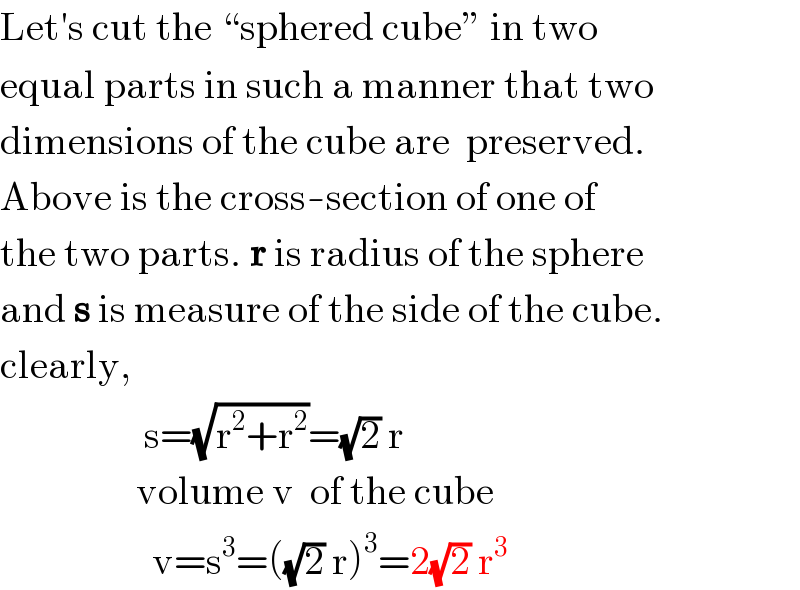
$$\mathrm{Let}'\mathrm{s}\:\mathrm{cut}\:\mathrm{the}\:“\mathrm{sphered}\:\mathrm{cube}''\:\mathrm{in}\:\mathrm{two} \\ $$$$\mathrm{equal}\:\mathrm{parts}\:\mathrm{in}\:\mathrm{such}\:\mathrm{a}\:\mathrm{manner}\:\mathrm{that}\:\mathrm{two} \\ $$$$\mathrm{dimensions}\:\mathrm{of}\:\mathrm{the}\:\mathrm{cube}\:\mathrm{are}\:\:\mathrm{preserved}. \\ $$$$\mathrm{Above}\:\mathrm{is}\:\mathrm{the}\:\mathrm{cross}-\mathrm{section}\:\mathrm{of}\:\mathrm{one}\:\mathrm{of} \\ $$$$\mathrm{the}\:\mathrm{two}\:\mathrm{parts}.\:\boldsymbol{\mathrm{r}}\:\mathrm{is}\:\mathrm{radius}\:\mathrm{of}\:\mathrm{the}\:\mathrm{sphere} \\ $$$$\mathrm{and}\:\boldsymbol{\mathrm{s}}\:\mathrm{is}\:\mathrm{measure}\:\mathrm{of}\:\mathrm{the}\:\mathrm{side}\:\mathrm{of}\:\mathrm{the}\:\mathrm{cube}. \\ $$$$\mathrm{clearly}, \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\mathrm{s}=\sqrt{\mathrm{r}^{\mathrm{2}} +\mathrm{r}^{\mathrm{2}} }=\sqrt{\mathrm{2}}\:\mathrm{r} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\mathrm{volume}\:\mathrm{v}\:\:\mathrm{of}\:\mathrm{the}\:\mathrm{cube} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\mathrm{v}=\mathrm{s}^{\mathrm{3}} =\left(\sqrt{\mathrm{2}}\:\mathrm{r}\right)^{\mathrm{3}} =\mathrm{2}\sqrt{\mathrm{2}}\:\mathrm{r}^{\mathrm{3}} \\ $$
