Menu Close

Question-54170

Tinku Tara 0 Comments
Pin




Question Number 54170 by ajfour last updated on 30/Jan/19
Commented by ajfour last updated on 30/Jan/19
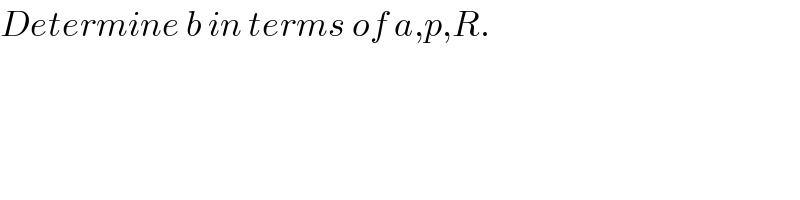
Determine b in terms of a,p,R.
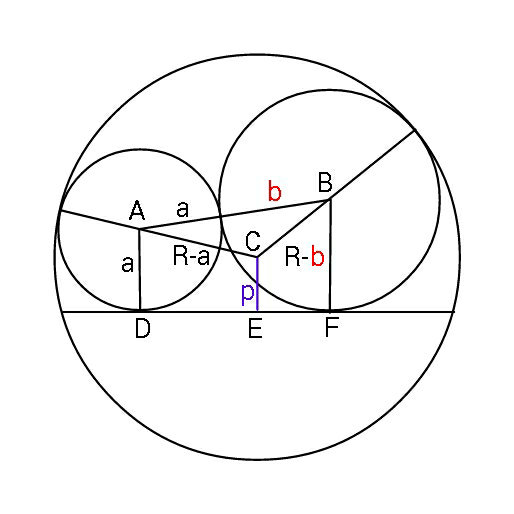
$${Determine}\:{b}\:{in}\:{terms}\:{of}\:{a},{p},{R}. \\ $$
Answered by ajfour last updated on 30/Jan/19
DF = (√((a+b)^2 −(b−a)^2 )) = 2(√(ab)) DE = (√((R−a)^2 −(a−p)^2 )) = (√((R−p)(R+p−2a))) EF = (√((R−b)^2 −(b−p)^2 )) = (√((R−p)(R+p−2b))) DE+EF = DF , ⇒ (√((R−p)(R+p−2a)))+(√((R−p)(R+p−2b))) = 2(√(ab)) let ((2a)/(R−p))=α , ((2b)/(R−p))=β , ((R+p)/(R−p)) = c . ⇒ (√(c−α))+(√(c−β)) =(√(αβ)) squaring 2c−(α+β)+2(√(c^2 −(α+β)c+αβ)) =αβ ⇒ 4(c^2 −(α+β)c+αβ)=(αβ−2c+α+β)^2 ⇒ 4c^2 −4c(α+β)+4αβ = α^2 β^2 +4c^2 +(α+β)^2 −4cαβ −2αβ(α+β)−4c(α+β) ⇒ (α−β)^2 +α^2 β^2 =2αβ(α+β+2c) ⇒ β^2 (α^2 −2α+1)−2α(1+α+2c)+α^2 =0 β = ((α(1+α+2c)+(√((1+α+2c)^2 −α^2 (α−1)^2 )))/((α−1)^2 )) ..
$${DF}\:=\:\sqrt{\left({a}+{b}\right)^{\mathrm{2}} −\left({b}−{a}\right)^{\mathrm{2}} }\:=\:\mathrm{2}\sqrt{{ab}} \\ $$$${DE}\:=\:\sqrt{\left({R}−{a}\right)^{\mathrm{2}} −\left({a}−{p}\right)^{\mathrm{2}} }\:=\:\sqrt{\left({R}−{p}\right)\left({R}+{p}−\mathrm{2}{a}\right)} \\ $$$${EF}\:=\:\sqrt{\left({R}−{b}\right)^{\mathrm{2}} −\left({b}−{p}\right)^{\mathrm{2}} }\:=\:\sqrt{\left({R}−{p}\right)\left({R}+{p}−\mathrm{2}{b}\right)} \\ $$$${DE}+{EF}\:=\:{DF}\:,\:\Rightarrow \\ $$$$\sqrt{\left({R}−{p}\right)\left({R}+{p}−\mathrm{2}{a}\right)}+\sqrt{\left({R}−{p}\right)\left({R}+{p}−\mathrm{2}{b}\right)} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:=\:\mathrm{2}\sqrt{{ab}} \\ $$$${let}\:\:\frac{\mathrm{2}{a}}{{R}−{p}}=\alpha\:,\:\:\frac{\mathrm{2}{b}}{{R}−{p}}=\beta\:,\:\:\frac{{R}+{p}}{{R}−{p}}\:=\:{c}\:. \\ $$$$\Rightarrow\:\sqrt{{c}−\alpha}+\sqrt{{c}−\beta}\:=\sqrt{\alpha\beta} \\ $$$${squaring} \\ $$$$\mathrm{2}{c}−\left(\alpha+\beta\right)+\mathrm{2}\sqrt{{c}^{\mathrm{2}} −\left(\alpha+\beta\right){c}+\alpha\beta}\:=\alpha\beta \\ $$$$\Rightarrow\:\mathrm{4}\left({c}^{\mathrm{2}} −\left(\alpha+\beta\right){c}+\alpha\beta\right)=\left(\alpha\beta−\mathrm{2}{c}+\alpha+\beta\right)^{\mathrm{2}} \\ $$$$\Rightarrow\:\mathrm{4}{c}^{\mathrm{2}} −\mathrm{4}{c}\left(\alpha+\beta\right)+\mathrm{4}\alpha\beta\: \\ $$$$\:\:\:\:\:\:=\:\alpha^{\mathrm{2}} \beta^{\mathrm{2}} +\mathrm{4}{c}^{\mathrm{2}} +\left(\alpha+\beta\right)^{\mathrm{2}} −\mathrm{4}{c}\alpha\beta\:\:\:\:\:\:\: \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:−\mathrm{2}\alpha\beta\left(\alpha+\beta\right)−\mathrm{4}{c}\left(\alpha+\beta\right) \\ $$$$\Rightarrow\:\left(\alpha−\beta\right)^{\mathrm{2}} +\alpha^{\mathrm{2}} \beta^{\mathrm{2}} =\mathrm{2}\alpha\beta\left(\alpha+\beta+\mathrm{2}{c}\right) \\ $$$$\Rightarrow \\ $$$$\beta^{\mathrm{2}} \left(\alpha^{\mathrm{2}} −\mathrm{2}\alpha+\mathrm{1}\right)−\mathrm{2}\alpha\left(\mathrm{1}+\alpha+\mathrm{2}{c}\right)+\alpha^{\mathrm{2}} =\mathrm{0} \\ $$$$\beta\:=\:\frac{\alpha\left(\mathrm{1}+\alpha+\mathrm{2}{c}\right)+\sqrt{\left(\mathrm{1}+\alpha+\mathrm{2}{c}\right)^{\mathrm{2}} −\alpha^{\mathrm{2}} \left(\alpha−\mathrm{1}\right)^{\mathrm{2}} }}{\left(\alpha−\mathrm{1}\right)^{\mathrm{2}} } \\ $$$$.. \\ $$
Commented by mr W last updated on 30/Jan/19
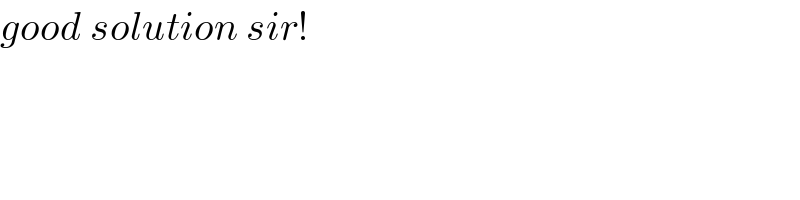
good solution sir!
$${good}\:{solution}\:{sir}! \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *