Question Number 119812 by I want to learn more last updated on 27/Oct/20

Answered by talminator2856791 last updated on 27/Oct/20
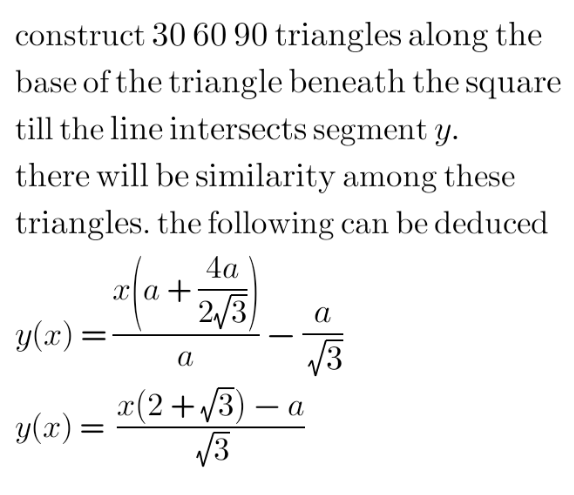
Answered by 1549442205PVT last updated on 27/Oct/20

Commented by 1549442205PVT last updated on 27/Oct/20

$$\mathrm{Given}\:\mathrm{AB}=\mathrm{AD}=\mathrm{AE}=\mathrm{DE}=\mathrm{BC}=\mathrm{a} \\ $$$$\mathrm{AH}=\mathrm{x}.\mathrm{Put}\:\mathrm{BF}=\mathrm{y}\Rightarrow\mathrm{y}\left(\mathrm{x}\right)=? \\ $$$$\mathrm{It}\:\mathrm{is}\:\mathrm{easy}\:\mathrm{to}\:\mathrm{see}\:\mathrm{that}\:\Delta\mathrm{CDE}\:\mathrm{is}\:\mathrm{isosceles} \\ $$$$\mathrm{at}\:\mathrm{D}\:\mathrm{with}\:\mathrm{DC}=\mathrm{DE}=\mathrm{a},\widehat {\mathrm{CDE}}=\mathrm{150}° \\ $$$$\widehat {\mathrm{DCE}}=\widehat {\mathrm{DEC}}=\mathrm{15}°.\mathrm{Since}\:\mathrm{tan15}°=\mathrm{2}−\sqrt{\mathrm{3}} \\ $$$$,\mathrm{in}\:\mathrm{the}\:\mathrm{right}\:\mathrm{triangle}\::\mathrm{DG}=\mathrm{a}\left(\mathrm{2}−\sqrt{\mathrm{3}}\right) \\ $$$$\mathrm{CG}=\sqrt{\mathrm{CD}^{\mathrm{2}} +\mathrm{DG}^{\mathrm{2}} }=\sqrt{\mathrm{a}^{\mathrm{2}} +\mathrm{a}^{\mathrm{2}} \left(\mathrm{7}−\mathrm{4}\sqrt{\mathrm{3}}\right)} \\ $$$$=\sqrt{\mathrm{a}^{\mathrm{2}} \left(\mathrm{8}−\mathrm{4}\sqrt{\mathrm{3}}\right)}=\mathrm{2a}\sqrt{\mathrm{2}−\sqrt{\mathrm{3}}} \\ $$$$\widehat {\mathrm{EDG}}=\mathrm{60}°\:\Rightarrow\mathrm{EG}^{\mathrm{2}} =\mathrm{a}^{\mathrm{2}} +\mathrm{a}^{\mathrm{2}} \left(\mathrm{7}−\mathrm{4}\sqrt{\mathrm{3}}\right)−\mathrm{2a}^{\mathrm{2}} \left(\mathrm{2}−\sqrt{\mathrm{3}}\right)\mathrm{cos60} \\ $$$$=\mathrm{a}^{\mathrm{2}} \left(\mathrm{8}−\mathrm{4}\sqrt{\mathrm{3}}\right)−\mathrm{a}^{\mathrm{2}} \left(\mathrm{2}−\sqrt{\mathrm{3}}\right)=\mathrm{a}^{\mathrm{2}} \left(\mathrm{6}−\mathrm{3}\sqrt{\mathrm{3}}\right) \\ $$$$\Rightarrow\mathrm{EG}=\mathrm{a}\sqrt{\mathrm{6}−\mathrm{3}\sqrt{\mathrm{3}}}=\mathrm{a}\sqrt{\mathrm{3}}\sqrt{\mathrm{2}−\sqrt{\mathrm{3}}} \\ $$$$\Rightarrow\mathrm{CE}=\mathrm{EG}+\mathrm{CG}=\mathrm{2a}\sqrt{\mathrm{2}−\sqrt{\mathrm{3}}}+\mathrm{a}\sqrt{\mathrm{3}}.\sqrt{\mathrm{2}−\sqrt{\mathrm{3}}} \\ $$$$\mathrm{CF}=\mathrm{a}−\mathrm{y},\mathrm{HG}=\mathrm{a}−\mathrm{x}−\mathrm{DG}=\mathrm{a}\left(\sqrt{\mathrm{3}}−\mathrm{1}\right)−\mathrm{x} \\ $$$$\mathrm{HG}//\mathrm{BC},\mathrm{so}\:\mathrm{by}\:\mathrm{Thalet}'\mathrm{s}\:\mathrm{therem}\:\mathrm{we}\:\mathrm{get} \\ $$$$\frac{\mathrm{HG}}{\mathrm{CF}}=\frac{\mathrm{EG}}{\mathrm{CE}}\Rightarrow\frac{\mathrm{a}\left(\sqrt{\mathrm{3}}−\mathrm{1}\right)−\mathrm{x}}{\mathrm{a}−\mathrm{y}}=\frac{\mathrm{a}\sqrt{\mathrm{6}−\mathrm{3}\sqrt{\mathrm{3}}}}{\mathrm{a}\left(\mathrm{2}\sqrt{\mathrm{2}−\sqrt{\mathrm{3}}}+\sqrt{\mathrm{3}}.\sqrt{\left.\mathrm{2}−\sqrt{\mathrm{3}}\right)}\right.} \\ $$$$=\frac{\sqrt{\mathrm{3}}\left(\sqrt{\left.\mathrm{2}−\sqrt{\mathrm{3}}\right)}\right.}{\left(\mathrm{2}+\sqrt{\mathrm{3}}\right)\sqrt{\mathrm{2}−\sqrt{\mathrm{3}}}}=\frac{\mathrm{1}}{\mathrm{2}+\sqrt{\mathrm{3}}}=\sqrt{\mathrm{3}}\left(\mathrm{2}−\sqrt{\mathrm{3}}\right) \\ $$$$\Rightarrow\mathrm{a}−\mathrm{y}=\frac{\mathrm{a}\left(\sqrt{\mathrm{3}}−\mathrm{1}\right)−\mathrm{x}}{\mathrm{2}\sqrt{\mathrm{3}}−\mathrm{3}} \\ $$$$\mathrm{y}=\mathrm{a}−\frac{\mathrm{a}\left(\sqrt{\mathrm{3}}−\mathrm{1}\right)−\mathrm{x}}{\mathrm{2}\sqrt{\mathrm{3}}−\mathrm{3}}=\frac{\mathrm{a}\left(\sqrt{\mathrm{3}}−\mathrm{2}\right)+\mathrm{x}}{\mathrm{2}\sqrt{\mathrm{3}}−\mathrm{3}} \\ $$$$\frac{\mathrm{x}}{\mathrm{2}\sqrt{\mathrm{3}}−\mathrm{3}}+\frac{\mathrm{a}\left(\sqrt{\mathrm{3}}−\mathrm{2}\right)}{\mathrm{2}\sqrt{\mathrm{3}}−\mathrm{3}}=\frac{\left(\mathrm{2}\sqrt{\mathrm{3}}+\mathrm{3}\right)\mathrm{x}}{\mathrm{3}}−\frac{\mathrm{a}\sqrt{\mathrm{3}}}{\mathrm{3}} \\ $$$$\mathrm{Thus}\:\mathrm{y}=\frac{\left(\mathrm{2}\sqrt{\mathrm{3}}+\mathrm{3}\right)\mathrm{x}}{\mathrm{3}}−\frac{\mathrm{a}\sqrt{\mathrm{3}}}{\mathrm{3}} \\ $$$$\boldsymbol{\mathrm{Second}}\:\boldsymbol{\mathrm{way}}: \\ $$$$\mathrm{Construct}\:\mathrm{the}\:\mathrm{coordinate}\:\mathrm{system}\:\mathrm{XOY} \\ $$$$\mathrm{so}\:\mathrm{that}\:\mathrm{A}\equiv\mathrm{O},\mathrm{OX}\equiv\left[\mathrm{AB}\right),\mathrm{OY}\equiv\mathrm{AD}.\mathrm{Then} \\ $$$$\mathrm{E}\left(−\frac{\mathrm{a}\sqrt{\mathrm{3}}}{\mathrm{2}},\frac{\mathrm{a}}{\mathrm{2}}\right),\mathrm{F}\left(\mathrm{a},\mathrm{y}\right).\mathrm{The}\:\mathrm{equation} \\ $$$$\mathrm{of}\:\mathrm{the}\:\mathrm{line}\:\mathrm{pass}\:\mathrm{through}\:\mathrm{EF}\:\mathrm{is} \\ $$$$\frac{\mathrm{Y}−\frac{\mathrm{a}}{\mathrm{2}}}{\mathrm{X}+\frac{\mathrm{a}\sqrt{\mathrm{3}}}{\mathrm{2}}}=\frac{\mathrm{y}−\frac{\mathrm{a}}{\mathrm{2}}}{\mathrm{a}+\frac{\mathrm{a}\sqrt{\mathrm{3}}}{\mathrm{2}}}\Rightarrow\frac{\mathrm{2Y}−\mathrm{a}}{\mathrm{2X}+\mathrm{a}\sqrt{\mathrm{3}}}=\frac{\mathrm{2y}−\mathrm{a}}{\mathrm{2a}+\mathrm{a}\sqrt{\mathrm{3}}} \\ $$$$\mathrm{The}\:\mathrm{this}\:\mathrm{line}\:\mathrm{pass}\:\mathrm{through}\:\mathrm{H}\left(\mathrm{0},\mathrm{x}\right)\:\mathrm{so} \\ $$$$\left(\mathrm{2a}+\mathrm{a}\sqrt{\mathrm{3}}\right)\left(\mathrm{2x}−\mathrm{a}\right)=\left(\mathrm{2y}−\mathrm{a}\right)\mathrm{a}\sqrt{\mathrm{3}} \\ $$$$\Rightarrow\left(\mathrm{2}+\sqrt{\mathrm{3}}\right)\mathrm{2x}−\mathrm{a}\left(\mathrm{2}+\sqrt{\mathrm{3}}\right)+\mathrm{a}\sqrt{\mathrm{3}}=\mathrm{2y}\sqrt{\mathrm{3}} \\ $$$$\Rightarrow\mathrm{y}=\frac{\mathrm{3}+\mathrm{2}\sqrt{\mathrm{3}}}{\mathrm{3}}\mathrm{x}−\frac{\mathrm{a}\sqrt{\mathrm{3}}}{\mathrm{3}} \\ $$
Commented by talminator2856791 last updated on 27/Oct/20

$$\:\mathrm{do}\:\mathrm{your}\:\mathrm{two}\:\mathrm{answers}\:\mathrm{simplify}\:\mathrm{to}\:\mathrm{the}\:\mathrm{same}\:\mathrm{thing}? \\ $$
Commented by talminator2856791 last updated on 27/Oct/20
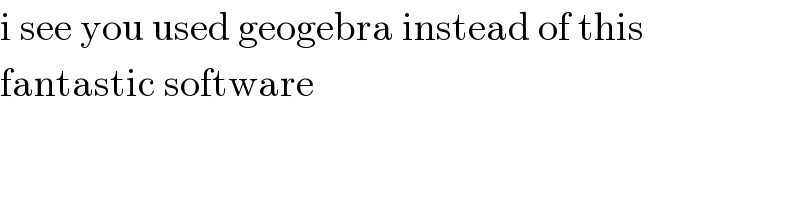
$$\mathrm{i}\:\mathrm{see}\:\mathrm{you}\:\mathrm{used}\:\mathrm{geogebra}\:\mathrm{instead}\:\mathrm{of}\:\mathrm{this} \\ $$$$\mathrm{fantastic}\:\mathrm{software} \\ $$
Commented by 1549442205PVT last updated on 27/Oct/20

$$\mathrm{Yes},\mathrm{it}\:\mathrm{is}\:\mathrm{right} \\ $$
Commented by I want to learn more last updated on 27/Oct/20

$$\mathrm{Wow},\:\mathrm{i}\:\mathrm{appreciate}\:\mathrm{sir}. \\ $$
