Question Number 185394 by mathlove last updated on 21/Jan/23
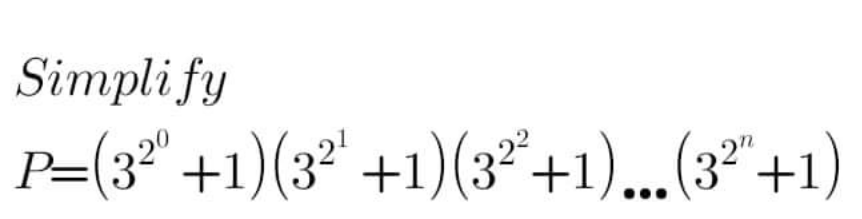
Answered by mr W last updated on 21/Jan/23
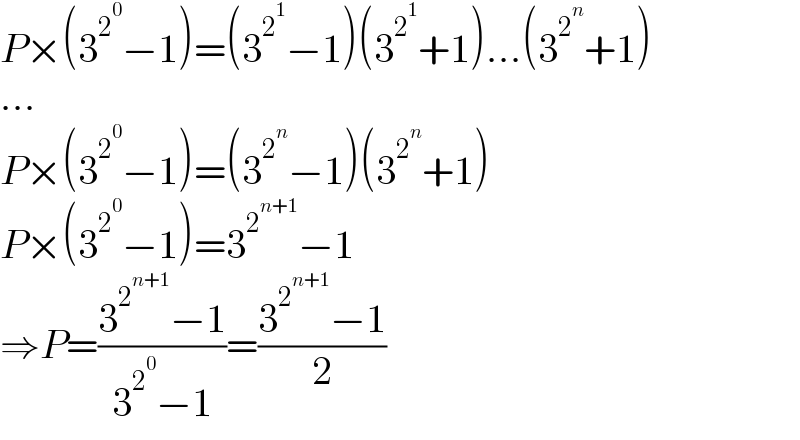
$${P}×\left(\mathrm{3}^{\mathrm{2}^{\mathrm{0}} } −\mathrm{1}\right)=\left(\mathrm{3}^{\mathrm{2}^{\mathrm{1}} } −\mathrm{1}\right)\left(\mathrm{3}^{\mathrm{2}^{\mathrm{1}} } +\mathrm{1}\right)…\left(\mathrm{3}^{\mathrm{2}^{{n}} } +\mathrm{1}\right) \\ $$$$… \\ $$$${P}×\left(\mathrm{3}^{\mathrm{2}^{\mathrm{0}} } −\mathrm{1}\right)=\left(\mathrm{3}^{\mathrm{2}^{{n}} } −\mathrm{1}\right)\left(\mathrm{3}^{\mathrm{2}^{{n}} } +\mathrm{1}\right) \\ $$$${P}×\left(\mathrm{3}^{\mathrm{2}^{\mathrm{0}} } −\mathrm{1}\right)=\mathrm{3}^{\mathrm{2}^{{n}+\mathrm{1}} } −\mathrm{1} \\ $$$$\Rightarrow{P}=\frac{\mathrm{3}^{\mathrm{2}^{{n}+\mathrm{1}} } −\mathrm{1}}{\mathrm{3}^{\mathrm{2}^{\mathrm{0}} } −\mathrm{1}}=\frac{\mathrm{3}^{\mathrm{2}^{{n}+\mathrm{1}} } −\mathrm{1}}{\mathrm{2}} \\ $$
Commented by mathlove last updated on 21/Jan/23

$${thanks} \\ $$
