Question-185424

Question Number 185424 by ajfour last updated on 21/Jan/23

Commented by Frix last updated on 21/Jan/23

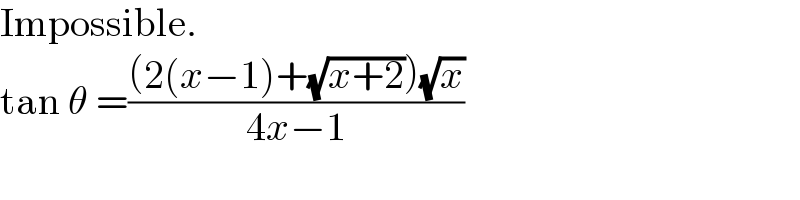
Impossible. tan θ =(((2(x−1)+(√(x+2)))(√x))/(4x−1))

$$\mathrm{Impossible}. \\ $$$$\mathrm{tan}\:\theta\:=\frac{\left(\mathrm{2}\left({x}−\mathrm{1}\right)+\sqrt{{x}+\mathrm{2}}\right)\sqrt{{x}}}{\mathrm{4}{x}−\mathrm{1}} \\ $$

Commented by MJS_new last updated on 22/Jan/23

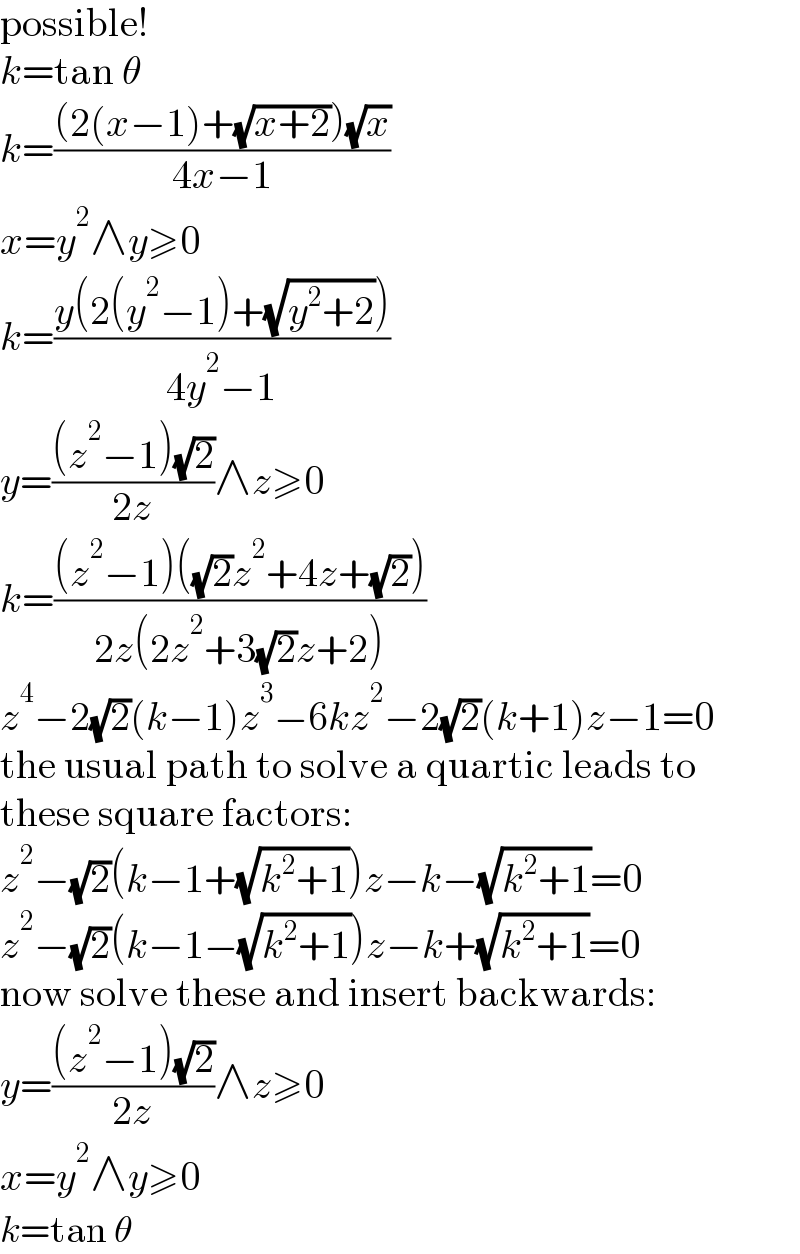
possible! k=tan θ k=(((2(x−1)+(√(x+2)))(√x))/(4x−1)) x=y^2 ∧y≥0 k=((y(2(y^2 −1)+(√(y^2 +2))))/(4y^2 −1)) y=(((z^2 −1)(√2))/(2z))∧z≥0 k=(((z^2 −1)((√2)z^2 +4z+(√2)))/(2z(2z^2 +3(√2)z+2))) z^4 −2(√2)(k−1)z^3 −6kz^2 −2(√2)(k+1)z−1=0 the usual path to solve a quartic leads to these square factors: z^2 −(√2)(k−1+(√(k^2 +1)))z−k−(√(k^2 +1))=0 z^2 −(√2)(k−1−(√(k^2 +1)))z−k+(√(k^2 +1))=0 now solve these and insert backwards: y=(((z^2 −1)(√2))/(2z))∧z≥0 x=y^2 ∧y≥0 k=tan θ

$$\mathrm{possible}! \\ $$$${k}=\mathrm{tan}\:\theta \\ $$$${k}=\frac{\left(\mathrm{2}\left({x}−\mathrm{1}\right)+\sqrt{{x}+\mathrm{2}}\right)\sqrt{{x}}}{\mathrm{4}{x}−\mathrm{1}} \\ $$$${x}={y}^{\mathrm{2}} \wedge{y}\geqslant\mathrm{0} \\ $$$${k}=\frac{{y}\left(\mathrm{2}\left({y}^{\mathrm{2}} −\mathrm{1}\right)+\sqrt{{y}^{\mathrm{2}} +\mathrm{2}}\right)}{\mathrm{4}{y}^{\mathrm{2}} −\mathrm{1}} \\ $$$${y}=\frac{\left({z}^{\mathrm{2}} −\mathrm{1}\right)\sqrt{\mathrm{2}}}{\mathrm{2}{z}}\wedge{z}\geqslant\mathrm{0} \\ $$$${k}=\frac{\left({z}^{\mathrm{2}} −\mathrm{1}\right)\left(\sqrt{\mathrm{2}}{z}^{\mathrm{2}} +\mathrm{4}{z}+\sqrt{\mathrm{2}}\right)}{\mathrm{2}{z}\left(\mathrm{2}{z}^{\mathrm{2}} +\mathrm{3}\sqrt{\mathrm{2}}{z}+\mathrm{2}\right)} \\ $$$${z}^{\mathrm{4}} −\mathrm{2}\sqrt{\mathrm{2}}\left({k}−\mathrm{1}\right){z}^{\mathrm{3}} −\mathrm{6}{kz}^{\mathrm{2}} −\mathrm{2}\sqrt{\mathrm{2}}\left({k}+\mathrm{1}\right){z}−\mathrm{1}=\mathrm{0} \\ $$$$\mathrm{the}\:\mathrm{usual}\:\mathrm{path}\:\mathrm{to}\:\mathrm{solve}\:\mathrm{a}\:\mathrm{quartic}\:\mathrm{leads}\:\mathrm{to} \\ $$$$\mathrm{these}\:\mathrm{square}\:\mathrm{factors}: \\ $$$${z}^{\mathrm{2}} −\sqrt{\mathrm{2}}\left({k}−\mathrm{1}+\sqrt{{k}^{\mathrm{2}} +\mathrm{1}}\right){z}−{k}−\sqrt{{k}^{\mathrm{2}} +\mathrm{1}}=\mathrm{0} \\ $$$${z}^{\mathrm{2}} −\sqrt{\mathrm{2}}\left({k}−\mathrm{1}−\sqrt{{k}^{\mathrm{2}} +\mathrm{1}}\right){z}−{k}+\sqrt{{k}^{\mathrm{2}} +\mathrm{1}}=\mathrm{0} \\ $$$$\mathrm{now}\:\mathrm{solve}\:\mathrm{these}\:\mathrm{and}\:\mathrm{insert}\:\mathrm{backwards}: \\ $$$${y}=\frac{\left({z}^{\mathrm{2}} −\mathrm{1}\right)\sqrt{\mathrm{2}}}{\mathrm{2}{z}}\wedge{z}\geqslant\mathrm{0} \\ $$$${x}={y}^{\mathrm{2}} \wedge{y}\geqslant\mathrm{0} \\ $$$${k}=\mathrm{tan}\:\theta \\ $$

Commented by Frix last updated on 21/Jan/23

$$\mathrm{Great}! \\ $$

Commented by ajfour last updated on 21/Jan/23

$${oh}\:{it}\:{created}\:{so}\:{much}\:{mess},\:{i}\:{am}\: \\ $$$${so}\:{glad}! \\ $$

Commented by MJS_new last updated on 21/Jan/23

have you found another solution? I first tried by squaring & transforming 2 times but this leads to 6^(th) grade polynom...

$$\mathrm{have}\:\mathrm{you}\:\mathrm{found}\:\mathrm{another}\:\mathrm{solution}? \\ $$$$\mathrm{I}\:\mathrm{first}\:\mathrm{tried}\:\mathrm{by}\:\mathrm{squaring}\:\&\:\mathrm{transforming}\:\mathrm{2} \\ $$$$\mathrm{times}\:\mathrm{but}\:\mathrm{this}\:\mathrm{leads}\:\mathrm{to}\:\mathrm{6}^{\mathrm{th}} \:\mathrm{grade}\:\mathrm{polynom}… \\ $$

Answered by mr W last updated on 21/Jan/23

(√((x+1)^2 −(x−1)^2 ))=tan (θ/2)+(x/(tan θ)) (x/(tan θ))−2(√x)+tan (θ/2)=0 ⇒(√x)=tan θ(1+(√(1−((tan (θ/2))/(tan θ))))) ⇒x=tan^2 θ (1+(√(1−((tan (θ/2))/(tan θ)))))^2

$$\sqrt{\left({x}+\mathrm{1}\right)^{\mathrm{2}} −\left({x}−\mathrm{1}\right)^{\mathrm{2}} }=\mathrm{tan}\:\frac{\theta}{\mathrm{2}}+\frac{{x}}{\mathrm{tan}\:\theta} \\ $$$$\frac{{x}}{\mathrm{tan}\:\theta}−\mathrm{2}\sqrt{{x}}+\mathrm{tan}\:\frac{\theta}{\mathrm{2}}=\mathrm{0} \\ $$$$\Rightarrow\sqrt{{x}}=\mathrm{tan}\:\theta\left(\mathrm{1}+\sqrt{\mathrm{1}−\frac{\mathrm{tan}\:\frac{\theta}{\mathrm{2}}}{\mathrm{tan}\:\theta}}\right) \\ $$$$\Rightarrow{x}=\mathrm{tan}^{\mathrm{2}} \:\theta\:\left(\mathrm{1}+\sqrt{\mathrm{1}−\frac{\mathrm{tan}\:\frac{\theta}{\mathrm{2}}}{\mathrm{tan}\:\theta}}\right)^{\mathrm{2}} \\ $$

Commented by MJS_new last updated on 21/Jan/23

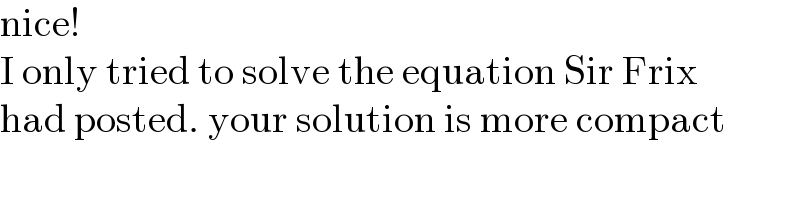
nice! I only tried to solve the equation Sir Frix had posted. your solution is more compact

$$\mathrm{nice}! \\ $$$$\mathrm{I}\:\mathrm{only}\:\mathrm{tried}\:\mathrm{to}\:\mathrm{solve}\:\mathrm{the}\:\mathrm{equation}\:\mathrm{Sir}\:\mathrm{Frix} \\ $$$$\mathrm{had}\:\mathrm{posted}.\:\mathrm{your}\:\mathrm{solution}\:\mathrm{is}\:\mathrm{more}\:\mathrm{compact} \\ $$

Commented by MJS_new last updated on 21/Jan/23

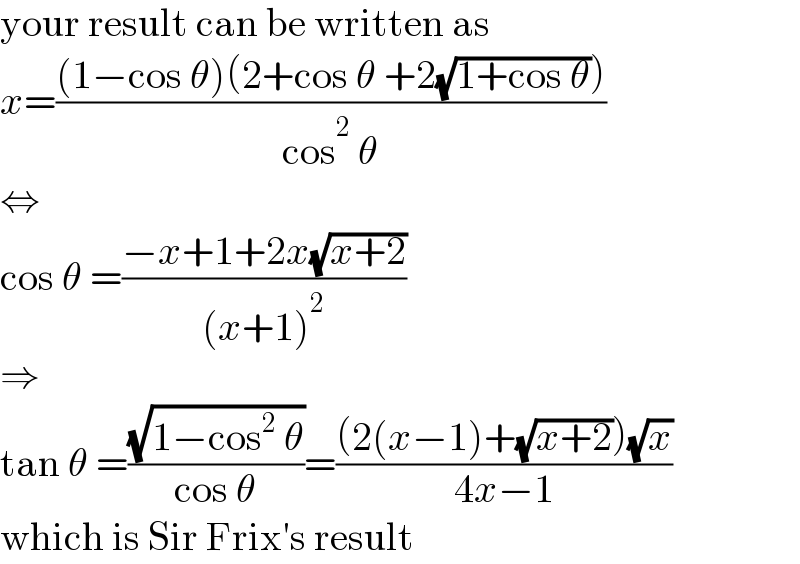
your result can be written as x=(((1−cos θ)(2+cos θ +2(√(1+cos θ))))/(cos^2 θ)) ⇔ cos θ =((−x+1+2x(√(x+2)))/((x+1)^2 )) ⇒ tan θ =((√(1−cos^2 θ))/(cos θ))=(((2(x−1)+(√(x+2)))(√x))/(4x−1)) which is Sir Frix′s result

$$\mathrm{your}\:\mathrm{result}\:\mathrm{can}\:\mathrm{be}\:\mathrm{written}\:\mathrm{as} \\ $$$${x}=\frac{\left(\mathrm{1}−\mathrm{cos}\:\theta\right)\left(\mathrm{2}+\mathrm{cos}\:\theta\:+\mathrm{2}\sqrt{\mathrm{1}+\mathrm{cos}\:\theta}\right)}{\mathrm{cos}^{\mathrm{2}} \:\theta} \\ $$$$\Leftrightarrow \\ $$$$\mathrm{cos}\:\theta\:=\frac{−{x}+\mathrm{1}+\mathrm{2}{x}\sqrt{{x}+\mathrm{2}}}{\left({x}+\mathrm{1}\right)^{\mathrm{2}} } \\ $$$$\Rightarrow \\ $$$$\mathrm{tan}\:\theta\:=\frac{\sqrt{\mathrm{1}−\mathrm{cos}^{\mathrm{2}} \:\theta}}{\mathrm{cos}\:\theta}=\frac{\left(\mathrm{2}\left({x}−\mathrm{1}\right)+\sqrt{{x}+\mathrm{2}}\right)\sqrt{{x}}}{\mathrm{4}{x}−\mathrm{1}} \\ $$$$\mathrm{which}\:\mathrm{is}\:\mathrm{Sir}\:\mathrm{Frix}'\mathrm{s}\:\mathrm{result} \\ $$

Commented by Ar Brandon last updated on 22/Jan/23

��

Commented by Rasheed.Sindhi last updated on 22/Jan/23

��

Commented by Spillover last updated on 23/Jan/23

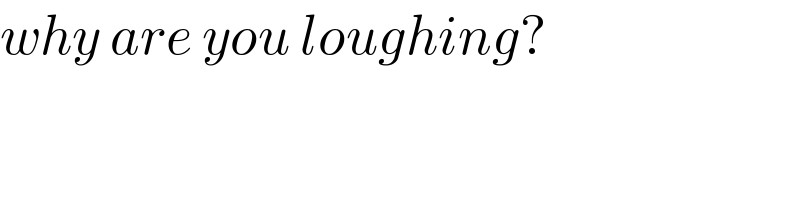
$${why}\:{are}\:{you}\:{loughing}?\: \\ $$

Commented by MJS_new last updated on 23/Jan/23

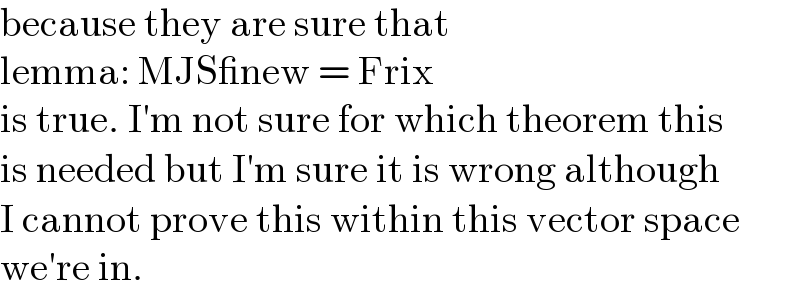
because they are sure that lemma: MJS_new = Frix is true. I′m not sure for which theorem this is needed but I′m sure it is wrong although I cannot prove this within this vector space we′re in.

$$\mathrm{because}\:\mathrm{they}\:\mathrm{are}\:\mathrm{sure}\:\mathrm{that} \\ $$$$\mathrm{lemma}:\:\mathrm{MJS\_new}\:=\:\mathrm{Frix} \\ $$$$\mathrm{is}\:\mathrm{true}.\:\mathrm{I}'\mathrm{m}\:\mathrm{not}\:\mathrm{sure}\:\mathrm{for}\:\mathrm{which}\:\mathrm{theorem}\:\mathrm{this} \\ $$$$\mathrm{is}\:\mathrm{needed}\:\mathrm{but}\:\mathrm{I}'\mathrm{m}\:\mathrm{sure}\:\mathrm{it}\:\mathrm{is}\:\mathrm{wrong}\:\mathrm{although} \\ $$$$\mathrm{I}\:\mathrm{cannot}\:\mathrm{prove}\:\mathrm{this}\:\mathrm{within}\:\mathrm{this}\:\mathrm{vector}\:\mathrm{space} \\ $$$$\mathrm{we}'\mathrm{re}\:\mathrm{in}. \\ $$

Commented by Frix last updated on 23/Jan/23

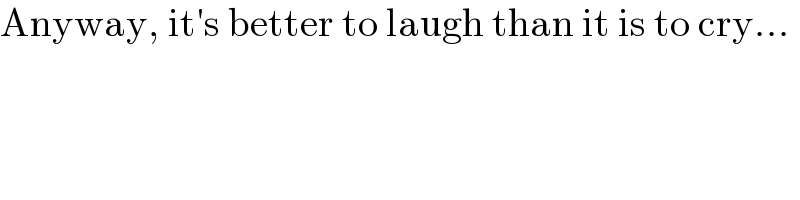
Anyway, it′s better to laugh than it is to cry...

$$\mathrm{Anyway},\:\mathrm{it}'\mathrm{s}\:\mathrm{better}\:\mathrm{to}\:\mathrm{laugh}\:\mathrm{than}\:\mathrm{it}\:\mathrm{is}\:\mathrm{to}\:\mathrm{cry}… \\ $$

Commented by Ar Brandon last updated on 23/Jan/23

Keep on entertaining us Sir MJFrix ��

Commented by Rasheed.Sindhi last updated on 23/Jan/23

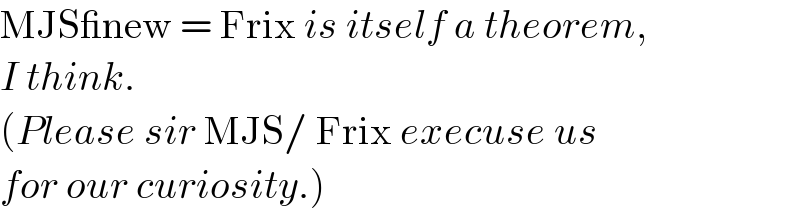
MJS_new = Frix is itself a theorem, I think. (Please sir MJS/ Frix execuse us for our curiosity.)

$$\mathrm{MJS\_new}\:=\:\mathrm{Frix}\:{is}\:{itself}\:{a}\:{theorem},\: \\ $$$${I}\:{think}. \\ $$$$\left({Please}\:{sir}\:\mathrm{MJS}/\:\mathrm{Frix}\:{execuse}\:{us}\:\right. \\ $$$$\left.{for}\:{our}\:{curiosity}.\right) \\ $$

Commented by MJS_new last updated on 23/Jan/23

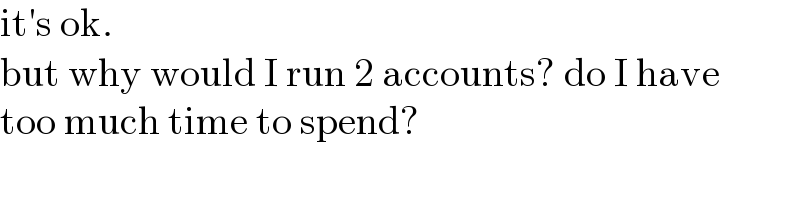
it′s ok. but why would I run 2 accounts? do I have too much time to spend?

$$\mathrm{it}'\mathrm{s}\:\mathrm{ok}. \\ $$$$\mathrm{but}\:\mathrm{why}\:\mathrm{would}\:\mathrm{I}\:\mathrm{run}\:\mathrm{2}\:\mathrm{accounts}?\:\mathrm{do}\:\mathrm{I}\:\mathrm{have} \\ $$$$\mathrm{too}\:\mathrm{much}\:\mathrm{time}\:\mathrm{to}\:\mathrm{spend}? \\ $$

Commented by Ar Brandon last updated on 23/Jan/23

Maybe her Majesty will be able to answer �� Good evening, sir MJFrix ��

Facebook Tweet Pin

Leave a Reply Cancel reply