Question Number 185800 by Rupesh123 last updated on 27/Jan/23
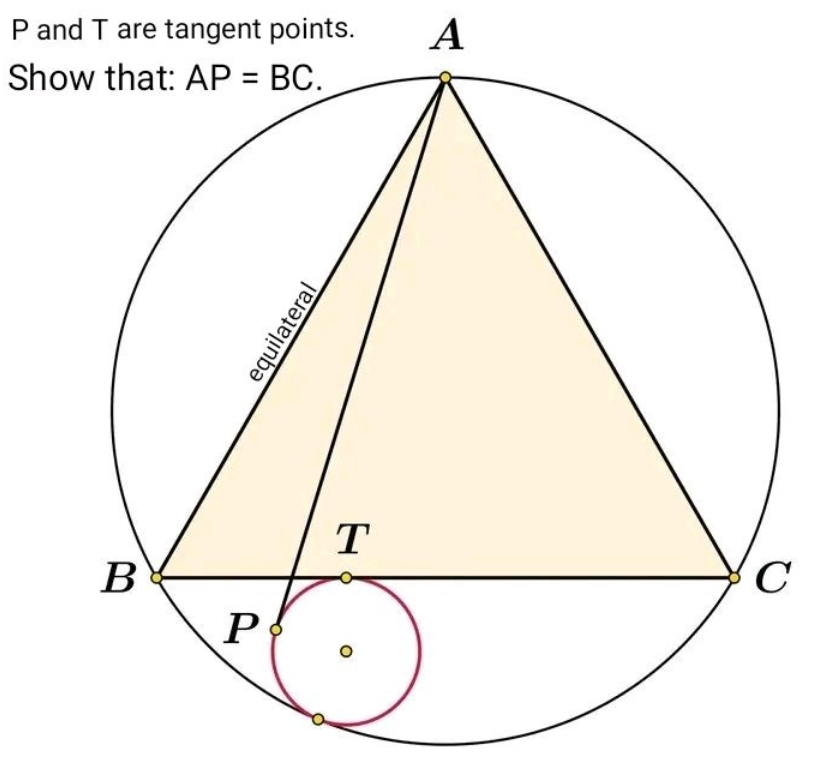
Answered by ajfour last updated on 27/Jan/23

$${let}\:{center}\:{of}\:{small}\:{circle}\:\left(−{h},−{k}\right) \\ $$$${hence}\:{eq}.\:\:\:\left({x}+{h}\right)^{\mathrm{2}} +\left({y}+{k}\right)^{\mathrm{2}} ={r}^{\mathrm{2}} \\ $$$${side}\:{of}\:{eql}.\:\:{triangle}\:{a}={R}\sqrt{\mathrm{3}} \\ $$$${length}\:{of}\:{tangent}\:{from}\:{A}\left(\mathrm{0},{R}\right) \\ $$$${is}\:\:{AP}\:=\sqrt{{h}^{\mathrm{2}} +\left({R}+{k}\right)^{\mathrm{2}} −{r}^{\mathrm{2}} }\:\:..\left({i}\right) \\ $$$${but}\:\:\:{k}=\frac{{R}}{\mathrm{2}}+{r}\:\:\:…\left({ii}\right) \\ $$$${and}\:\:\:{h}^{\mathrm{2}} +{k}^{\mathrm{2}} =\left({R}−{r}\right)^{\mathrm{2}} \:\:\:…\left({iii}\right) \\ $$$${using}\:\left({ii}\right)\:{and}\:\left({iii}\right)\:{in}\:\left({i}\right) \\ $$$${AP}^{\:\mathrm{2}} =\:\left({R}−{r}\right)^{\mathrm{2}} +{R}^{\mathrm{2}} −{r}^{\mathrm{2}} +\mathrm{2}{R}\left(\frac{{R}}{\mathrm{2}}+{r}\right) \\ $$$$\Rightarrow\:{AP}\:^{\mathrm{2}} =\:\:\:\mathrm{3}{R}^{\mathrm{2}} \\ $$$${AP}\:=\:{R}\sqrt{\mathrm{3}}\:=\:{BC} \\ $$
Commented by mr W last updated on 28/Jan/23

$${nice}\:{approach}! \\ $$
Answered by mr W last updated on 28/Jan/23

Commented by mr W last updated on 28/Jan/23

$${R}={radius}\:{of}\:{big}\:{circle} \\ $$$${r}={radius}\:{of}\:{small}\:{circle} \\ $$$${OQ}=\frac{{R}}{\mathrm{2}} \\ $$$${BC}=\sqrt{\mathrm{3}}{R} \\ $$$$\left({AS}^{\mathrm{2}} =\right){AP}^{\mathrm{2}} +{r}^{\mathrm{2}} =\left({R}+\frac{{R}}{\mathrm{2}}+{r}\right)^{\mathrm{2}} +\left({R}−{r}\right)^{\mathrm{2}} −\left(\frac{{R}}{\mathrm{2}}+{r}\right)^{\mathrm{2}} \\ $$$${AP}^{\mathrm{2}} =\mathrm{3}{R}^{\mathrm{2}} \\ $$$$\Rightarrow{AP}=\sqrt{\mathrm{3}}{R}={BC}\:\checkmark \\ $$
