Question Number 70915 by Mr. K last updated on 09/Oct/19

Commented by Mr. K last updated on 09/Oct/19

$${The}\:{circles}\:{have}\:{the}\:{same}\:{radius}.\: \\ $$$${The}\:{triangle}\:{is}\:{equilateral}\:{side} \\ $$$$\mathrm{28}\left(\mathrm{1}+\sqrt{\mathrm{3}}\right).\:{Determine}\:{the}\:{radius} \\ $$$${of}\:{the}\:{circumferences}. \\ $$
Answered by mind is power last updated on 09/Oct/19
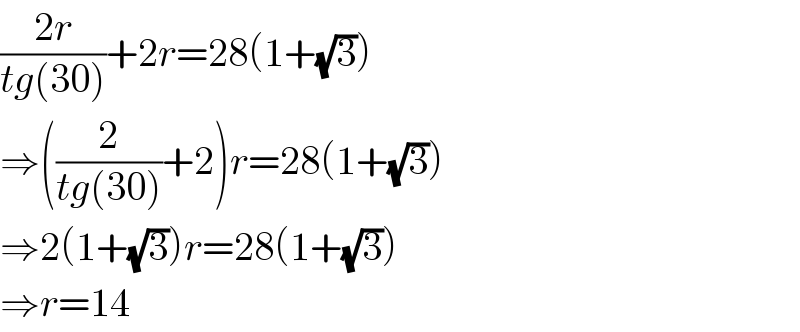
$$\frac{\mathrm{2}{r}}{{tg}\left(\mathrm{30}\right)}+\mathrm{2}{r}=\mathrm{28}\left(\mathrm{1}+\sqrt{\mathrm{3}}\right) \\ $$$$\Rightarrow\left(\frac{\mathrm{2}}{{tg}\left(\mathrm{30}\right)}+\mathrm{2}\right){r}=\mathrm{28}\left(\mathrm{1}+\sqrt{\mathrm{3}}\right) \\ $$$$\Rightarrow\mathrm{2}\left(\mathrm{1}+\sqrt{\mathrm{3}}\right){r}=\mathrm{28}\left(\mathrm{1}+\sqrt{\mathrm{3}}\right) \\ $$$$\Rightarrow{r}=\mathrm{14} \\ $$
