Question Number 120355 by TITA last updated on 30/Oct/20

Commented by TITA last updated on 30/Oct/20

$${please}\:{help} \\ $$
Commented by TITA last updated on 30/Oct/20

$${please}\:{help} \\ $$
Answered by john santu last updated on 30/Oct/20
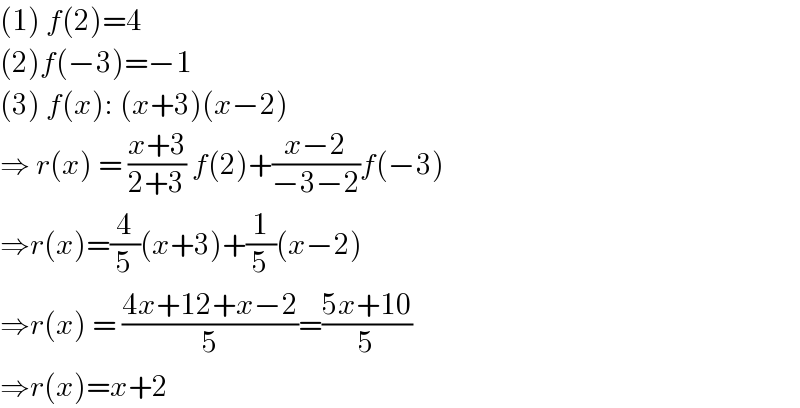
$$\left(\mathrm{1}\right)\:{f}\left(\mathrm{2}\right)=\mathrm{4} \\ $$$$\left(\mathrm{2}\right){f}\left(−\mathrm{3}\right)=−\mathrm{1} \\ $$$$\left(\mathrm{3}\right)\:{f}\left({x}\right):\:\left({x}+\mathrm{3}\right)\left({x}−\mathrm{2}\right) \\ $$$$\Rightarrow\:{r}\left({x}\right)\:=\:\frac{{x}+\mathrm{3}}{\mathrm{2}+\mathrm{3}}\:{f}\left(\mathrm{2}\right)+\frac{{x}−\mathrm{2}}{−\mathrm{3}−\mathrm{2}}{f}\left(−\mathrm{3}\right) \\ $$$$\Rightarrow{r}\left({x}\right)=\frac{\mathrm{4}}{\mathrm{5}}\left({x}+\mathrm{3}\right)+\frac{\mathrm{1}}{\mathrm{5}}\left({x}−\mathrm{2}\right) \\ $$$$\Rightarrow{r}\left({x}\right)\:=\:\frac{\mathrm{4}{x}+\mathrm{12}+{x}−\mathrm{2}}{\mathrm{5}}=\frac{\mathrm{5}{x}+\mathrm{10}}{\mathrm{5}} \\ $$$$\Rightarrow{r}\left({x}\right)={x}+\mathrm{2} \\ $$
Commented by TITA last updated on 30/Oct/20

$${thank}\:{sir} \\ $$$$ \\ $$
Answered by benjo_mathlover last updated on 30/Oct/20

$${in}\:{other}\:{way}\: \\ $$$${let}\:{f}\left({x}\right)\:=\:{g}\left({x}\right)\left({x}+\mathrm{3}\right)\left({x}−\mathrm{2}\right)+{px}+{q} \\ $$$${where}\:{px}+{q}\:{is}\:{remainder}\:{when}\:{f}\left({x}\right)\:{divided} \\ $$$${by}\:{x}^{\mathrm{2}} +{x}−\mathrm{6} \\ $$$${for}\:{x}=\mathrm{2}\Rightarrow\mathrm{2}{p}+{q}=\mathrm{4} \\ $$$${for}\:{x}=−\mathrm{3}\Rightarrow−\mathrm{3}{p}+{q}=−\mathrm{1} \\ $$$$\begin{pmatrix}{\:\:\:\mathrm{2}\:\:\:\:\:\:\mathrm{1}}\\{−\mathrm{3}\:\:\:\:\mathrm{1}}\end{pmatrix}\:\begin{pmatrix}{{p}}\\{{q}}\end{pmatrix}\:=\:\begin{pmatrix}{\:\:\:\mathrm{4}}\\{−\mathrm{1}}\end{pmatrix} \\ $$$$\rightarrow\begin{cases}{{p}=\frac{\begin{vmatrix}{\:\:\:\mathrm{4}\:\:\:\:\:\:\:\mathrm{1}}\\{−\mathrm{1}\:\:\:\:\:\mathrm{1}}\end{vmatrix}}{\mathrm{5}}=\:\frac{\mathrm{5}}{\mathrm{5}}=\mathrm{1}}\\{{q}=\frac{\begin{vmatrix}{\:\:\:\:\mathrm{2}\:\:\:\:\:\:\mathrm{4}}\\{−\mathrm{3}\:\:\:\:−\mathrm{1}}\end{vmatrix}}{\mathrm{5}}=\frac{\mathrm{10}}{\mathrm{5}}=\mathrm{2}}\end{cases} \\ $$$${thus}\:{r}\left({x}\right)=\mathrm{1}.{x}+\mathrm{2}={x}+\mathrm{2} \\ $$
Answered by mathmax by abdo last updated on 30/Oct/20

$$\mathrm{f}\left(\mathrm{x}\right)=\left(\mathrm{x}−\mathrm{2}\right)\mathrm{q}\left(\mathrm{x}\right)+\mathrm{4}\:\mathrm{and}\:\mathrm{f}\left(\mathrm{x}\right)=\left(\mathrm{x}+\mathrm{3}\right)\mathrm{v}\left(\mathrm{x}\right)−\mathrm{1}\:\Rightarrow \\ $$$$\mathrm{f}\left(\mathrm{2}\right)=\mathrm{4}\:\mathrm{and}\:\mathrm{f}\left(−\mathrm{3}\right)=−\mathrm{1} \\ $$$$\mathrm{f}\left(\mathrm{x}\right)=\mathrm{h}\left(\mathrm{x}\right)\left(\mathrm{x}^{\mathrm{2}} +\mathrm{x}−\mathrm{6}\right)+\mathrm{ax}+\mathrm{b} \\ $$$$\mathrm{we}\:\mathrm{have}\:\mathrm{f}\left(\mathrm{2}\right)\:=\mathrm{2a}+\mathrm{b}=\mathrm{4}\:\mathrm{and}\:\mathrm{f}\left(−\mathrm{3}\right)=−\mathrm{3a}+\mathrm{b}\:=−\mathrm{1}\:\Rightarrow \\ $$$$\begin{cases}{\mathrm{2a}+\mathrm{b}=\mathrm{4}}\\{\mathrm{3a}−\mathrm{b}=\mathrm{1}\:\Rightarrow\begin{cases}{\mathrm{5a}=\mathrm{5}}\\{\mathrm{b}=\mathrm{4}−\mathrm{2a}\:\Rightarrow\begin{cases}{\mathrm{a}=\mathrm{1}}\\{\mathrm{b}=\mathrm{2}\:\Rightarrow}\end{cases}}\end{cases}}\end{cases} \\ $$$$\mathrm{f}\left(\mathrm{x}\right)=\mathrm{h}\left(\mathrm{x}^{\mathrm{2}} +\mathrm{x}−\mathrm{6}\right)+\mathrm{x}+\mathrm{2}\:\Rightarrow\mathrm{r}\left(\mathrm{x}\right)=\mathrm{x}+\mathrm{2} \\ $$
