Menu Close

1-x-2-x-dx-

Tinku Tara 0 Comments
Pin




Question Number 120374 by bramlexs22 last updated on 31/Oct/20
∫ ((√(1+x^2 ))/x) dx
$$\:\:\:\:\int\:\frac{\sqrt{\mathrm{1}+{x}^{\mathrm{2}} }}{{x}}\:{dx}\: \\ $$
Answered by Lordose last updated on 31/Oct/20
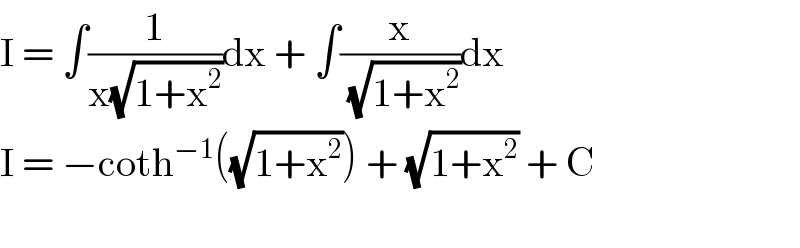
I = ∫(1/(x(√(1+x^2 ))))dx + ∫(x/( (√(1+x^2 ))))dx I = −coth^(−1) ((√(1+x^2 ))) + (√(1+x^2 )) + C
$$\mathrm{I}\:=\:\int\frac{\mathrm{1}}{\mathrm{x}\sqrt{\mathrm{1}+\mathrm{x}^{\mathrm{2}} }}\mathrm{dx}\:+\:\int\frac{\mathrm{x}}{\:\sqrt{\mathrm{1}+\mathrm{x}^{\mathrm{2}} }}\mathrm{dx} \\ $$$$\mathrm{I}\:=\:−\mathrm{coth}^{−\mathrm{1}} \left(\sqrt{\mathrm{1}+\mathrm{x}^{\mathrm{2}} }\right)\:+\:\sqrt{\mathrm{1}+\mathrm{x}^{\mathrm{2}} }\:+\:\mathrm{C} \\ $$$$ \\ $$
Answered by john santu last updated on 31/Oct/20
∫ ((1+x^2 )/(x(√(1+x^2 )))) dx =∫ (1/(x(√(1+x^2 )))) dx + ∫ (x/( (√(1+x^2 )))) dx I_1 = ∫ (1/(x(√(1+x^2 )))) dx = ∫ ((sec^2 q dq)/(tan q. sec q)) [ x = tan q ] I_1 = ∫ ((sec q dq)/(tan q)) = ∫ (1/(cos q))×((cos q)/(sin q)) dq I_1 = ∫ cosec q dq = ln ∣cosec q−cot q ∣+c_1 I_1 = ln ∣(((√(1+x^2 ))−1)/x)∣ +c_1 I_2 = ∫ (x/( (√(1+x^2 )))) dx = (1/2)∫ ((d(1+x^2 ))/( (√(1+x^2 ))))= (√(1+x^2 )) + c_2 I=I_1 +I_2 = ln ∣(((√(1+x^2 ))−1)/x)∣ + (√(1+x^2 )) + C
$$\int\:\frac{\mathrm{1}+{x}^{\mathrm{2}} }{{x}\sqrt{\mathrm{1}+{x}^{\mathrm{2}} }}\:{dx}\:=\int\:\frac{\mathrm{1}}{{x}\sqrt{\mathrm{1}+{x}^{\mathrm{2}} }}\:{dx}\:+\:\int\:\frac{{x}}{\:\sqrt{\mathrm{1}+{x}^{\mathrm{2}} }}\:{dx} \\ $$$${I}_{\mathrm{1}} =\:\int\:\frac{\mathrm{1}}{{x}\sqrt{\mathrm{1}+{x}^{\mathrm{2}} }}\:{dx}\:=\:\int\:\frac{\mathrm{sec}\:^{\mathrm{2}} {q}\:{dq}}{\mathrm{tan}\:{q}.\:\mathrm{sec}\:{q}}\:\:\left[\:{x}\:=\:\mathrm{tan}\:{q}\:\right] \\ $$$${I}_{\mathrm{1}} =\:\int\:\frac{\mathrm{sec}\:{q}\:{dq}}{\mathrm{tan}\:{q}}\:=\:\int\:\frac{\mathrm{1}}{\mathrm{cos}\:{q}}×\frac{\mathrm{cos}\:{q}}{\mathrm{sin}\:{q}}\:{dq} \\ $$$${I}_{\mathrm{1}} =\:\int\:\mathrm{cosec}\:{q}\:{dq}\:=\:\mathrm{ln}\:\mid\mathrm{cosec}\:{q}−\mathrm{cot}\:{q}\:\mid+{c}_{\mathrm{1}} \\ $$$${I}_{\mathrm{1}} =\:\mathrm{ln}\:\mid\frac{\sqrt{\mathrm{1}+{x}^{\mathrm{2}} }−\mathrm{1}}{{x}}\mid\:+{c}_{\mathrm{1}} \\ $$$${I}_{\mathrm{2}} =\:\int\:\frac{{x}}{\:\sqrt{\mathrm{1}+{x}^{\mathrm{2}} }}\:{dx}\:=\:\frac{\mathrm{1}}{\mathrm{2}}\int\:\frac{{d}\left(\mathrm{1}+{x}^{\mathrm{2}} \right)}{\:\sqrt{\mathrm{1}+{x}^{\mathrm{2}} }}=\:\sqrt{\mathrm{1}+{x}^{\mathrm{2}} }\:+\:{c}_{\mathrm{2}} \\ $$$${I}={I}_{\mathrm{1}} +{I}_{\mathrm{2}} =\:\mathrm{ln}\:\mid\frac{\sqrt{\mathrm{1}+{x}^{\mathrm{2}} }−\mathrm{1}}{{x}}\mid\:+\:\sqrt{\mathrm{1}+{x}^{\mathrm{2}} }\:+\:{C} \\ $$
Answered by mathmax by abdo last updated on 01/Nov/20
A =∫ ((√(1+x^2 ))/x)dx we do tbe changement x=sht ⇒ A =∫ ((cht)/(sht))cht dt =∫ ((ch^2 t)/(sht))dt =∫ ((1+ch(2t))/(2sht))dt =(1/2)∫ ((1+((e^(2t) +e^(−2t) )/2))/((e^t −e^(−t) )/2))dt =(1/2)∫ ((2+e^(2t) +e^(−2t) )/(e^t −e^(−t) ))dt ⇒2A =_(e^t =u) ∫ ((2+u^2 +u^(−2) )/(u−u^(−1) ))(du/u) =∫ ((u^2 +u^(−2) +2)/(u^2 −1))du =∫ ((u^4 +1+2u^2 )/(u^4 −u^2 ))du =∫ ((u^4 −u^2 +3u^2 +1)/(u^4 −u^2 ))du =u +∫ ((3u^2 +1)/(u^2 (u^2 −1)))du let decompose F(u)=((3u^2 +1)/(u^2 (u−1)(u+1))) F(u) =(a/u)+(b/u^2 ) +(c/(u−1))+(d/(u+1)) b=−1 , c=(4/2)=2 ,d =(4/(−2))=−2 ⇒F(u)=(a/u)−(1/u^2 )+(2/(u−1)) −(2/(u+1)) lim_(u→+∞) uF(u)=0 =a+2−2 ⇒a=0 ⇒F(u)=−(1/u^2 )+(2/(u−1))−(2/(u+1)) ⇒ 2A =u+(1/u) +2ln∣u−1∣−2ln∣u+1∣ +c u =e^t and t=argsh(x)=ln(x+(√(1+x^2 ))) ⇒u=x+(√(1+x^2 )) 2A =x+(√(1+x^2 ))+2ln∣x+(√(1+x^2 ))−1∣−2ln∣x+(√(1+x^2 ))+1∣ +c ⇒ A =(1/2)(x+(√(1+x^2 )))+ln∣((x−1+(√(1+x^2 )))/(x+1+(√(1+x^2 ))))∣ +C
$$\mathrm{A}\:=\int\:\:\frac{\sqrt{\mathrm{1}+\mathrm{x}^{\mathrm{2}} }}{\mathrm{x}}\mathrm{dx}\:\:\mathrm{we}\:\mathrm{do}\:\mathrm{tbe}\:\mathrm{changement}\:\mathrm{x}=\mathrm{sht}\:\Rightarrow \\ $$$$\mathrm{A}\:=\int\:\:\frac{\mathrm{cht}}{\mathrm{sht}}\mathrm{cht}\:\mathrm{dt}\:=\int\:\:\frac{\mathrm{ch}^{\mathrm{2}} \mathrm{t}}{\mathrm{sht}}\mathrm{dt}\:=\int\:\:\frac{\mathrm{1}+\mathrm{ch}\left(\mathrm{2t}\right)}{\mathrm{2sht}}\mathrm{dt} \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}}\int\:\:\frac{\mathrm{1}+\frac{\mathrm{e}^{\mathrm{2t}} +\mathrm{e}^{−\mathrm{2t}} }{\mathrm{2}}}{\frac{\mathrm{e}^{\mathrm{t}} −\mathrm{e}^{−\mathrm{t}} }{\mathrm{2}}}\mathrm{dt}\:=\frac{\mathrm{1}}{\mathrm{2}}\int\:\:\frac{\mathrm{2}+\mathrm{e}^{\mathrm{2t}} +\mathrm{e}^{−\mathrm{2t}} }{\mathrm{e}^{\mathrm{t}} −\mathrm{e}^{−\mathrm{t}} }\mathrm{dt} \\ $$$$\Rightarrow\mathrm{2A}\:=_{\mathrm{e}^{\mathrm{t}} =\mathrm{u}} \:\:\:\int\:\:\:\frac{\mathrm{2}+\mathrm{u}^{\mathrm{2}} +\mathrm{u}^{−\mathrm{2}} }{\mathrm{u}−\mathrm{u}^{−\mathrm{1}} }\frac{\mathrm{du}}{\mathrm{u}}\:=\int\:\:\frac{\mathrm{u}^{\mathrm{2}} +\mathrm{u}^{−\mathrm{2}} \:+\mathrm{2}}{\mathrm{u}^{\mathrm{2}} −\mathrm{1}}\mathrm{du} \\ $$$$=\int\:\:\frac{\mathrm{u}^{\mathrm{4}} \:+\mathrm{1}+\mathrm{2u}^{\mathrm{2}} }{\mathrm{u}^{\mathrm{4}} −\mathrm{u}^{\mathrm{2}} }\mathrm{du}\:=\int\:\:\frac{\mathrm{u}^{\mathrm{4}} −\mathrm{u}^{\mathrm{2}} \:+\mathrm{3u}^{\mathrm{2}} \:+\mathrm{1}}{\mathrm{u}^{\mathrm{4}} −\mathrm{u}^{\mathrm{2}} }\mathrm{du} \\ $$$$=\mathrm{u}\:+\int\:\:\frac{\mathrm{3u}^{\mathrm{2}} \:+\mathrm{1}}{\mathrm{u}^{\mathrm{2}} \left(\mathrm{u}^{\mathrm{2}} −\mathrm{1}\right)}\mathrm{du}\:\:\mathrm{let}\:\mathrm{decompose}\:\mathrm{F}\left(\mathrm{u}\right)=\frac{\mathrm{3u}^{\mathrm{2}} \:+\mathrm{1}}{\mathrm{u}^{\mathrm{2}} \left(\mathrm{u}−\mathrm{1}\right)\left(\mathrm{u}+\mathrm{1}\right)} \\ $$$$\mathrm{F}\left(\mathrm{u}\right)\:=\frac{\mathrm{a}}{\mathrm{u}}+\frac{\mathrm{b}}{\mathrm{u}^{\mathrm{2}} }\:+\frac{\mathrm{c}}{\mathrm{u}−\mathrm{1}}+\frac{\mathrm{d}}{\mathrm{u}+\mathrm{1}} \\ $$$$\mathrm{b}=−\mathrm{1}\:,\:\mathrm{c}=\frac{\mathrm{4}}{\mathrm{2}}=\mathrm{2}\:,\mathrm{d}\:=\frac{\mathrm{4}}{−\mathrm{2}}=−\mathrm{2}\:\Rightarrow\mathrm{F}\left(\mathrm{u}\right)=\frac{\mathrm{a}}{\mathrm{u}}−\frac{\mathrm{1}}{\mathrm{u}^{\mathrm{2}} }+\frac{\mathrm{2}}{\mathrm{u}−\mathrm{1}}\:−\frac{\mathrm{2}}{\mathrm{u}+\mathrm{1}} \\ $$$$\mathrm{lim}_{\mathrm{u}\rightarrow+\infty} \mathrm{uF}\left(\mathrm{u}\right)=\mathrm{0}\:=\mathrm{a}+\mathrm{2}−\mathrm{2}\:\Rightarrow\mathrm{a}=\mathrm{0}\:\Rightarrow\mathrm{F}\left(\mathrm{u}\right)=−\frac{\mathrm{1}}{\mathrm{u}^{\mathrm{2}} }+\frac{\mathrm{2}}{\mathrm{u}−\mathrm{1}}−\frac{\mathrm{2}}{\mathrm{u}+\mathrm{1}}\:\Rightarrow \\ $$$$\mathrm{2A}\:=\mathrm{u}+\frac{\mathrm{1}}{\mathrm{u}}\:+\mathrm{2ln}\mid\mathrm{u}−\mathrm{1}\mid−\mathrm{2ln}\mid\mathrm{u}+\mathrm{1}\mid\:+\mathrm{c} \\ $$$$\mathrm{u}\:=\mathrm{e}^{\mathrm{t}} \:\mathrm{and}\:\mathrm{t}=\mathrm{argsh}\left(\mathrm{x}\right)=\mathrm{ln}\left(\mathrm{x}+\sqrt{\mathrm{1}+\mathrm{x}^{\mathrm{2}} }\right)\:\Rightarrow\mathrm{u}=\mathrm{x}+\sqrt{\mathrm{1}+\mathrm{x}^{\mathrm{2}} } \\ $$$$\mathrm{2A}\:=\mathrm{x}+\sqrt{\mathrm{1}+\mathrm{x}^{\mathrm{2}} }+\mathrm{2ln}\mid\mathrm{x}+\sqrt{\mathrm{1}+\mathrm{x}^{\mathrm{2}} }−\mathrm{1}\mid−\mathrm{2ln}\mid\mathrm{x}+\sqrt{\mathrm{1}+\mathrm{x}^{\mathrm{2}} }+\mathrm{1}\mid\:+\mathrm{c}\:\Rightarrow \\ $$$$\mathrm{A}\:=\frac{\mathrm{1}}{\mathrm{2}}\left(\mathrm{x}+\sqrt{\mathrm{1}+\mathrm{x}^{\mathrm{2}} }\right)+\mathrm{ln}\mid\frac{\mathrm{x}−\mathrm{1}+\sqrt{\mathrm{1}+\mathrm{x}^{\mathrm{2}} }}{\mathrm{x}+\mathrm{1}+\sqrt{\mathrm{1}+\mathrm{x}^{\mathrm{2}} }}\mid\:+\mathrm{C} \\ $$$$ \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *