Question Number 186021 by Spillover last updated on 30/Jan/23
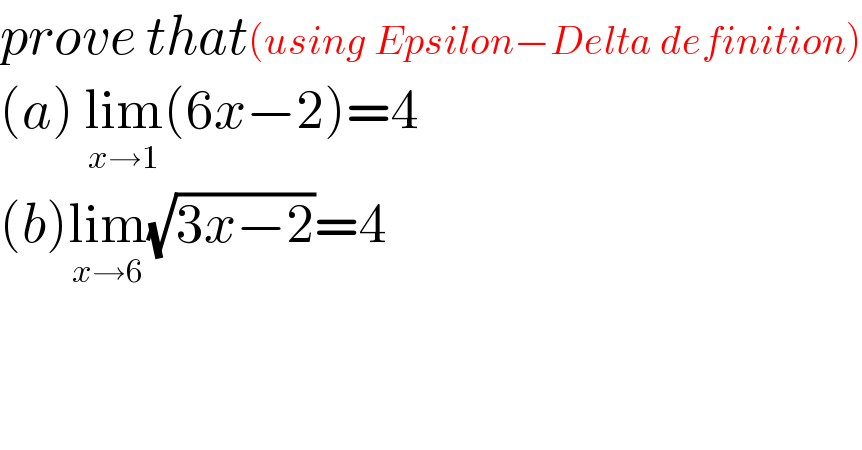
$${prove}\:{that}\left({using}\:{Epsilon}−{Delta}\:{definition}\right) \\ $$$$\left({a}\right)\:\underset{{x}\rightarrow\mathrm{1}} {\mathrm{lim}}\left(\mathrm{6}{x}−\mathrm{2}\right)=\mathrm{4} \\ $$$$\left({b}\right)\underset{{x}\rightarrow\mathrm{6}} {\mathrm{lim}}\sqrt{\mathrm{3}{x}−\mathrm{2}}=\mathrm{4} \\ $$
Answered by aba last updated on 30/Jan/23
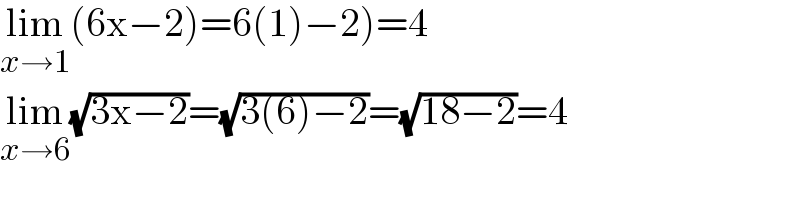
$$\left.\underset{{x}\rightarrow\mathrm{1}} {\mathrm{lim}}\left(\mathrm{6x}−\mathrm{2}\right)=\mathrm{6}\left(\mathrm{1}\right)−\mathrm{2}\right)=\mathrm{4} \\ $$$$\underset{{x}\rightarrow\mathrm{6}} {\mathrm{lim}}\sqrt{\mathrm{3x}−\mathrm{2}}=\sqrt{\mathrm{3}\left(\mathrm{6}\right)−\mathrm{2}}=\sqrt{\mathrm{18}−\mathrm{2}}=\mathrm{4} \\ $$
