Question Number 120544 by rubygarfield last updated on 01/Nov/20
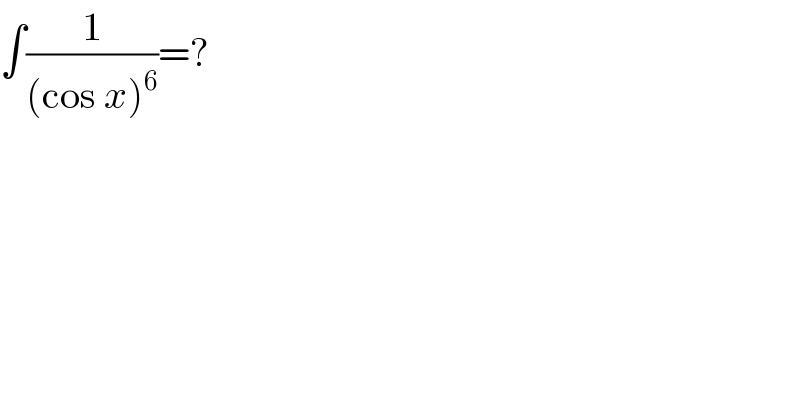
$$\int\frac{\mathrm{1}}{\left(\mathrm{cos}\:{x}\right)^{\mathrm{6}} }=? \\ $$
Answered by Dwaipayan Shikari last updated on 01/Nov/20
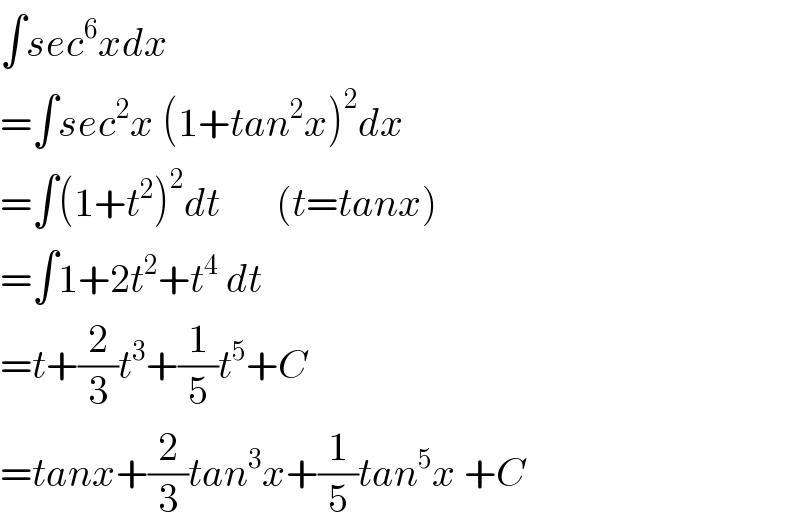
$$\int{sec}^{\mathrm{6}} {xdx} \\ $$$$=\int{sec}^{\mathrm{2}} {x}\:\left(\mathrm{1}+{tan}^{\mathrm{2}} {x}\right)^{\mathrm{2}} {dx} \\ $$$$=\int\left(\mathrm{1}+{t}^{\mathrm{2}} \right)^{\mathrm{2}} {dt}\:\:\:\:\:\:\:\left({t}={tanx}\right) \\ $$$$=\int\mathrm{1}+\mathrm{2}{t}^{\mathrm{2}} +{t}^{\mathrm{4}} \:{dt} \\ $$$$={t}+\frac{\mathrm{2}}{\mathrm{3}}{t}^{\mathrm{3}} +\frac{\mathrm{1}}{\mathrm{5}}{t}^{\mathrm{5}} +{C} \\ $$$$={tanx}+\frac{\mathrm{2}}{\mathrm{3}}{tan}^{\mathrm{3}} {x}+\frac{\mathrm{1}}{\mathrm{5}}{tan}^{\mathrm{5}} {x}\:+{C} \\ $$
Commented by peter frank last updated on 01/Nov/20

$$\mathrm{thank}\:\mathrm{you} \\ $$
