Prove-or-disprove-that-minimum-value-of-n-which-satisfies-the-equation-10-n-1-mod-7-p-is-n-6-7-p-1-

Tinku Tara June 3, 2023 Number Theory 0 Comments

Question Number 443 by prakash jain last updated on 04/Jan/15

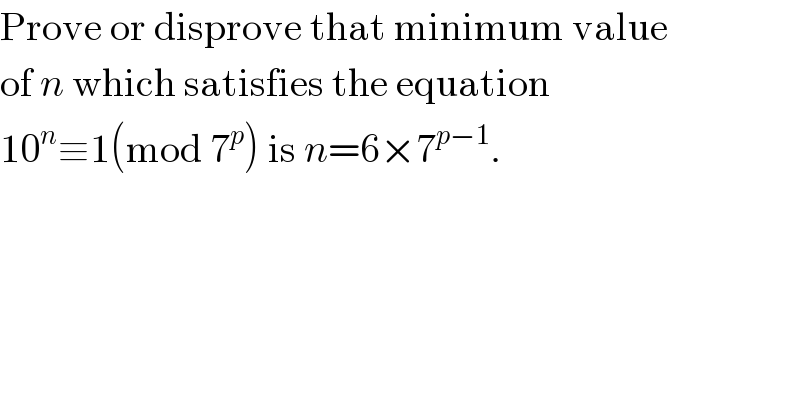
Prove or disprove that minimum value of n which satisfies the equation 10^n ≡1(mod 7^p ) is n=6×7^(p−1) .

$$\mathrm{Prove}\:\mathrm{or}\:\mathrm{disprove}\:\mathrm{that}\:\mathrm{minimum}\:\mathrm{value} \\ $$$$\mathrm{of}\:{n}\:\mathrm{which}\:\mathrm{satisfies}\:\mathrm{the}\:\mathrm{equation} \\ $$$$\mathrm{10}^{{n}} \equiv\mathrm{1}\left(\mathrm{mod}\:\mathrm{7}^{{p}} \right)\:\mathrm{is}\:{n}=\mathrm{6}×\mathrm{7}^{{p}−\mathrm{1}} . \\ $$

Commented by 123456 last updated on 05/Jan/15

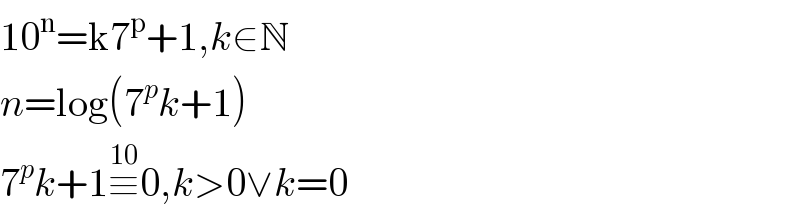
10^n =k7^p +1,k∈N n=log(7^p k+1) 7^p k+1≡^(10) 0,k>0∨k=0

$$\mathrm{10}^{\mathrm{n}} =\mathrm{k7}^{\mathrm{p}} +\mathrm{1},{k}\in\mathbb{N} \\ $$$${n}=\mathrm{log}\left(\mathrm{7}^{{p}} {k}+\mathrm{1}\right) \\ $$$$\mathrm{7}^{{p}} {k}+\mathrm{1}\overset{\mathrm{10}} {\equiv}\mathrm{0},{k}>\mathrm{0}\vee{k}=\mathrm{0} \\ $$

Facebook Tweet Pin

Prove-or-disprove-that-minimum-value-of-n-which-satisfies-the-equation-10-n-1-mod-7-p-is-n-6-7-p-1-

Leave a Reply Cancel reply