Question Number 186300 by mnjuly1970 last updated on 03/Feb/23
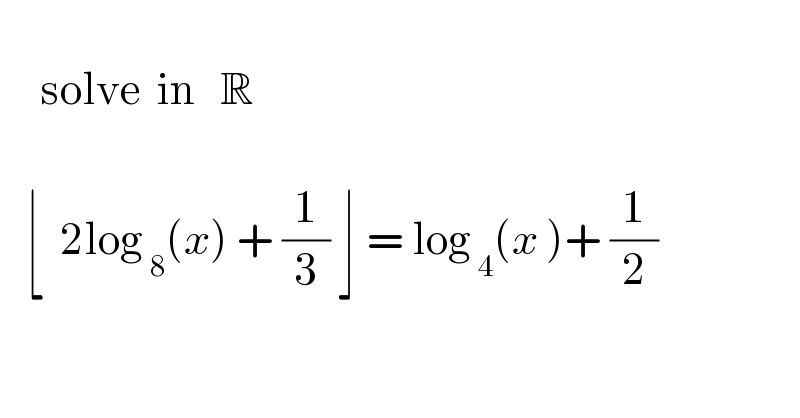
$$\:\:\: \\ $$$$\:\:\:\:\:\mathrm{solve}\:\:\mathrm{in}\:\:\:\mathbb{R} \\ $$$$ \\ $$$$\:\:\:\lfloor\:\:\mathrm{2log}_{\:\mathrm{8}} \left({x}\right)\:+\:\frac{\mathrm{1}}{\mathrm{3}}\:\rfloor\:=\:\mathrm{log}_{\:\mathrm{4}} \left({x}\:\right)+\:\frac{\mathrm{1}}{\mathrm{2}} \\ $$$$ \\ $$
Answered by MJS_new last updated on 03/Feb/23
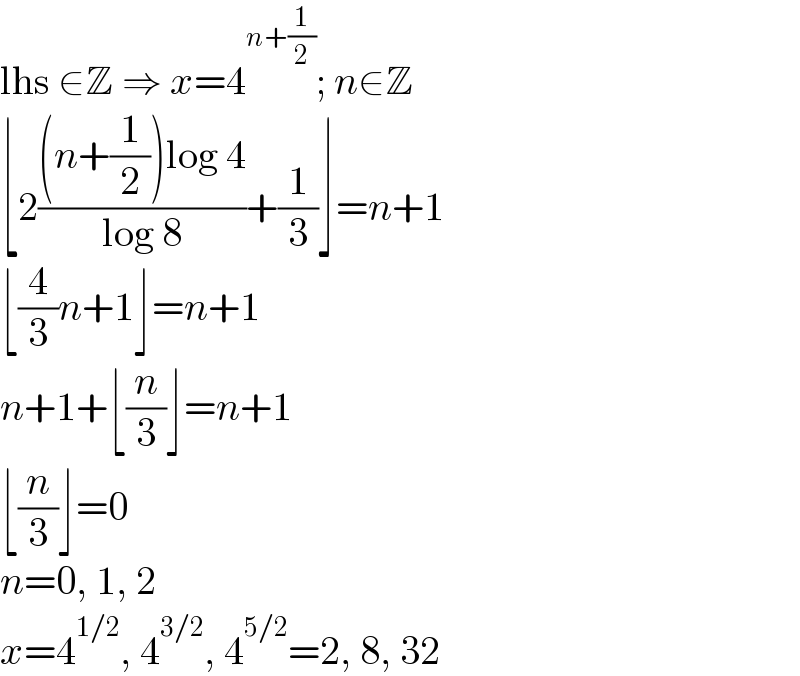
$$\mathrm{lhs}\:\in\mathbb{Z}\:\Rightarrow\:{x}=\mathrm{4}^{{n}+\frac{\mathrm{1}}{\mathrm{2}}} ;\:{n}\in\mathbb{Z} \\ $$$$\lfloor\mathrm{2}\frac{\left({n}+\frac{\mathrm{1}}{\mathrm{2}}\right)\mathrm{log}\:\mathrm{4}}{\mathrm{log}\:\mathrm{8}}+\frac{\mathrm{1}}{\mathrm{3}}\rfloor={n}+\mathrm{1} \\ $$$$\lfloor\frac{\mathrm{4}}{\mathrm{3}}{n}+\mathrm{1}\rfloor={n}+\mathrm{1} \\ $$$${n}+\mathrm{1}+\lfloor\frac{{n}}{\mathrm{3}}\rfloor={n}+\mathrm{1} \\ $$$$\lfloor\frac{{n}}{\mathrm{3}}\rfloor=\mathrm{0} \\ $$$${n}=\mathrm{0},\:\mathrm{1},\:\mathrm{2} \\ $$$${x}=\mathrm{4}^{\mathrm{1}/\mathrm{2}} ,\:\mathrm{4}^{\mathrm{3}/\mathrm{2}} ,\:\mathrm{4}^{\mathrm{5}/\mathrm{2}} =\mathrm{2},\:\mathrm{8},\:\mathrm{32} \\ $$
Commented by mnjuly1970 last updated on 03/Feb/23
$${thanks}\:{alot}\:\:{sir}\:.\:{very}\:{nice}\:{solution} \\ $$
Commented by MJS_new last updated on 03/Feb/23

$$\mathrm{you}'\mathrm{re}\:\mathrm{welcome} \\ $$
