Question Number 5422 by love math last updated on 14/May/16
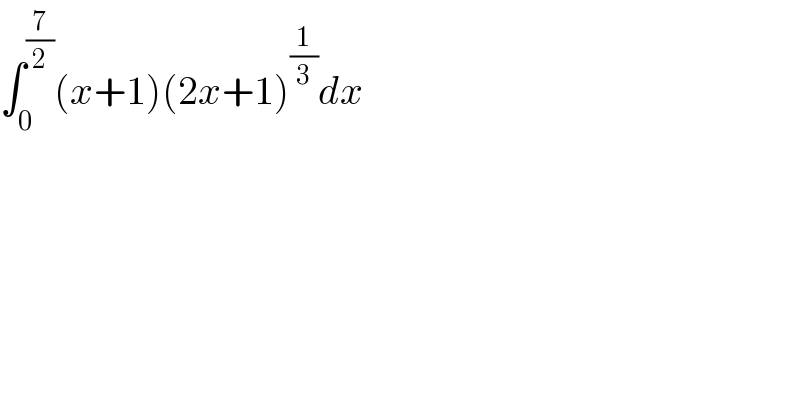
$$\int_{\mathrm{0}} ^{\frac{\mathrm{7}}{\mathrm{2}}} \left({x}+\mathrm{1}\right)\left(\mathrm{2}{x}+\mathrm{1}\right)^{\frac{\mathrm{1}}{\mathrm{3}}} {dx} \\ $$
Answered by nchejane last updated on 14/May/16
![=[(3/8)(x+1)(2x+1)^(4/3) ]_0 ^(7/2) −(3/8)∫_0 ^(7/2) (2x+1)^(4/3) dx =[(3/8)(x+1)(2x+2)^(4/3) ]_0 ^(7/2) −[(9/(28))(2x+1)^(7/3) ]_0 ^(7/2) =....](https://www.tinkutara.com/question/Q5432.png)
$$=\left[\frac{\mathrm{3}}{\mathrm{8}}\left({x}+\mathrm{1}\right)\left(\mathrm{2}{x}+\mathrm{1}\right)^{\frac{\mathrm{4}}{\mathrm{3}}} \right]_{\mathrm{0}} ^{\frac{\mathrm{7}}{\mathrm{2}}} −\frac{\mathrm{3}}{\mathrm{8}}\int_{\mathrm{0}} ^{\frac{\mathrm{7}}{\mathrm{2}}} \left(\mathrm{2}{x}+\mathrm{1}\right)^{\frac{\mathrm{4}}{\mathrm{3}}} {dx} \\ $$$$=\left[\frac{\mathrm{3}}{\mathrm{8}}\left({x}+\mathrm{1}\right)\left(\mathrm{2}{x}+\mathrm{2}\right)^{\frac{\mathrm{4}}{\mathrm{3}}} \right]_{\mathrm{0}} ^{\frac{\mathrm{7}}{\mathrm{2}}} −\left[\frac{\mathrm{9}}{\mathrm{28}}\left(\mathrm{2}{x}+\mathrm{1}\right)^{\frac{\mathrm{7}}{\mathrm{3}}} \right]_{\mathrm{0}} ^{\frac{\mathrm{7}}{\mathrm{2}}} \\ $$$$=…. \\ $$
