Question Number 136500 by rexford last updated on 22/Mar/21

Answered by Dwaipayan Shikari last updated on 22/Mar/21
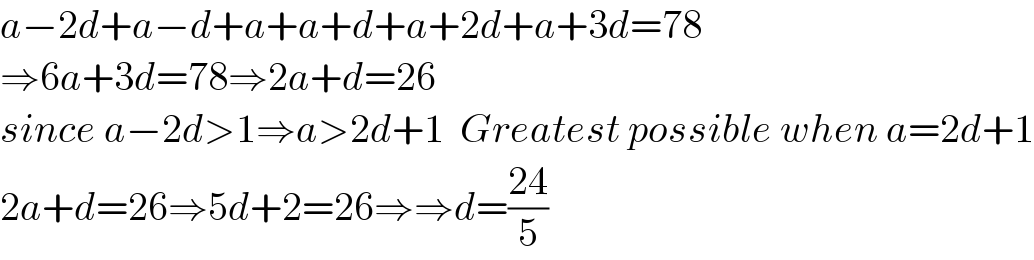
$${a}−\mathrm{2}{d}+{a}−{d}+{a}+{a}+{d}+{a}+\mathrm{2}{d}+{a}+\mathrm{3}{d}=\mathrm{78} \\ $$$$\Rightarrow\mathrm{6}{a}+\mathrm{3}{d}=\mathrm{78}\Rightarrow\mathrm{2}{a}+{d}=\mathrm{26} \\ $$$${since}\:{a}−\mathrm{2}{d}>\mathrm{1}\Rightarrow{a}>\mathrm{2}{d}+\mathrm{1}\:\:{Greatest}\:{possible}\:{when}\:{a}=\mathrm{2}{d}+\mathrm{1} \\ $$$$\mathrm{2}{a}+{d}=\mathrm{26}\Rightarrow\mathrm{5}{d}+\mathrm{2}=\mathrm{26}\Rightarrow\Rightarrow{d}=\frac{\mathrm{24}}{\mathrm{5}} \\ $$
Commented by rexford last updated on 22/Mar/21
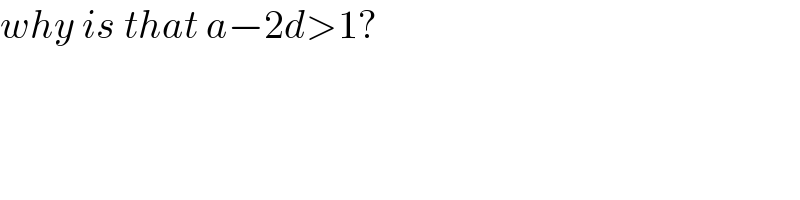
$${why}\:{is}\:{that}\:{a}−\mathrm{2}{d}>\mathrm{1}? \\ $$
Answered by MJS_new last updated on 23/Mar/21
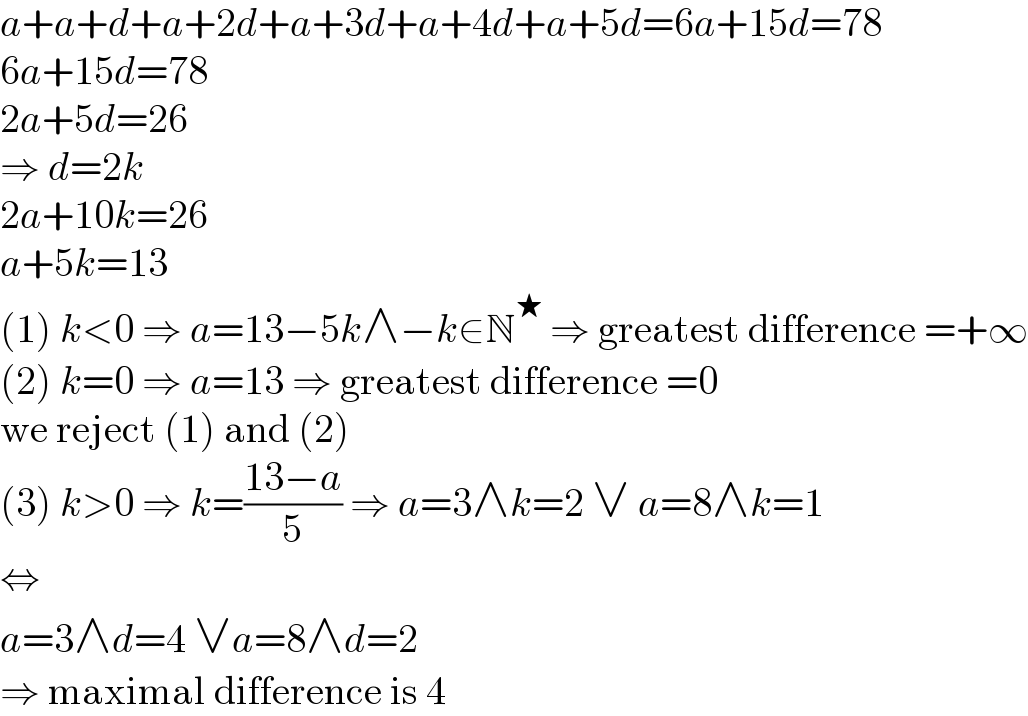
$${a}+{a}+{d}+{a}+\mathrm{2}{d}+{a}+\mathrm{3}{d}+{a}+\mathrm{4}{d}+{a}+\mathrm{5}{d}=\mathrm{6}{a}+\mathrm{15}{d}=\mathrm{78} \\ $$$$\mathrm{6}{a}+\mathrm{15}{d}=\mathrm{78} \\ $$$$\mathrm{2}{a}+\mathrm{5}{d}=\mathrm{26} \\ $$$$\Rightarrow\:{d}=\mathrm{2}{k} \\ $$$$\mathrm{2}{a}+\mathrm{10}{k}=\mathrm{26} \\ $$$${a}+\mathrm{5}{k}=\mathrm{13} \\ $$$$\left(\mathrm{1}\right)\:{k}<\mathrm{0}\:\Rightarrow\:{a}=\mathrm{13}−\mathrm{5}{k}\wedge−{k}\in\mathbb{N}^{\bigstar} \:\Rightarrow\:\mathrm{greatest}\:\mathrm{difference}\:=+\infty \\ $$$$\left(\mathrm{2}\right)\:{k}=\mathrm{0}\:\Rightarrow\:{a}=\mathrm{13}\:\Rightarrow\:\mathrm{greatest}\:\mathrm{difference}\:=\mathrm{0} \\ $$$$\mathrm{we}\:\mathrm{reject}\:\left(\mathrm{1}\right)\:\mathrm{and}\:\left(\mathrm{2}\right) \\ $$$$\left(\mathrm{3}\right)\:{k}>\mathrm{0}\:\Rightarrow\:{k}=\frac{\mathrm{13}−{a}}{\mathrm{5}}\:\Rightarrow\:{a}=\mathrm{3}\wedge{k}=\mathrm{2}\:\vee\:{a}=\mathrm{8}\wedge{k}=\mathrm{1} \\ $$$$\Leftrightarrow \\ $$$${a}=\mathrm{3}\wedge{d}=\mathrm{4}\:\vee{a}=\mathrm{8}\wedge{d}=\mathrm{2} \\ $$$$\Rightarrow\:\mathrm{maximal}\:\mathrm{difference}\:\mathrm{is}\:\mathrm{4} \\ $$
