Question Number 445 by 123456 last updated on 05/Jan/15
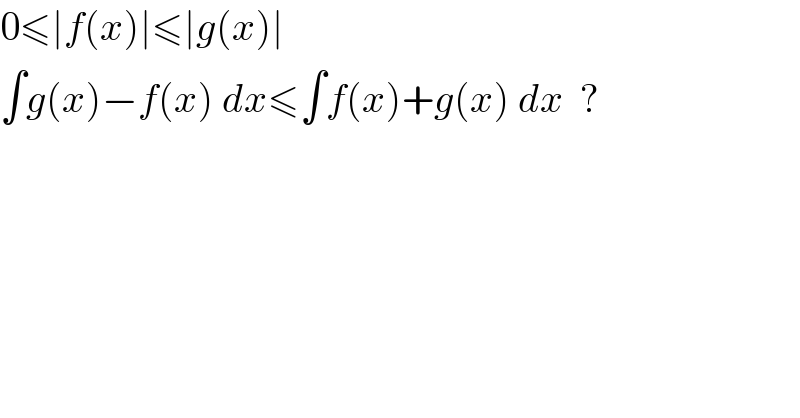
$$\mathrm{0}\leqslant\mid{f}\left({x}\right)\mid\leqslant\mid{g}\left({x}\right)\mid \\ $$$$\int{g}\left({x}\right)−{f}\left({x}\right)\:{dx}\leqslant\int{f}\left({x}\right)+{g}\left({x}\right)\:{dx}\:\:? \\ $$
Commented by prakash jain last updated on 05/Jan/15

$${f}\left({x}\right)=−\mathrm{1} \\ $$$${g}\left({x}\right)=\mathrm{1} \\ $$$$\mid{f}\left({x}\right)\mid=\mathrm{1} \\ $$$$\mid{g}\left({x}\right)\mid=\mathrm{1} \\ $$$${g}\left({x}\right)−{f}\left({x}\right)=\mathrm{2} \\ $$$${f}\left({x}\right)+{g}\left({x}\right)=\mathrm{0} \\ $$
