Menu Close

Question-55467

Tinku Tara 0 Comments
Pin




Question Number 55467 by peter frank last updated on 24/Feb/19
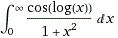
Commented by tanmay.chaudhury50@gmail.com last updated on 25/Feb/19
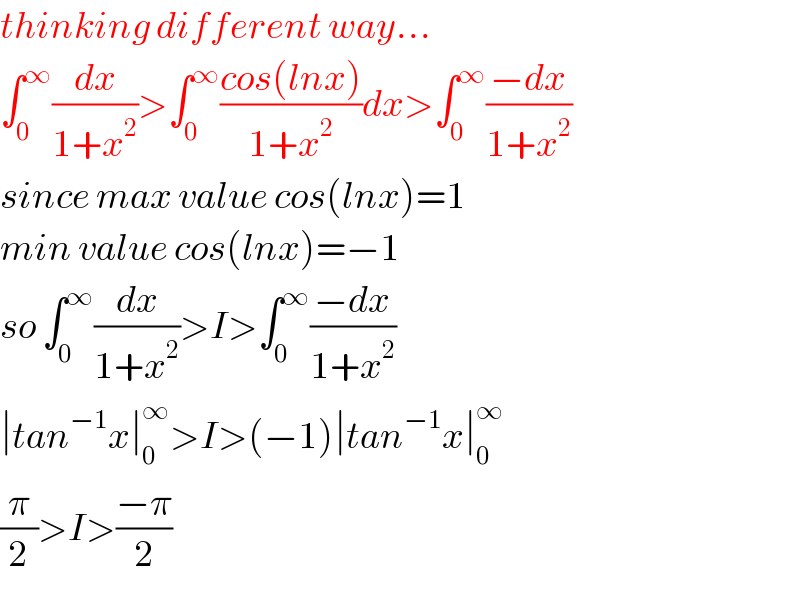
thinking different way... ∫_0 ^∞ (dx/(1+x^2 ))>∫_0 ^∞ ((cos(lnx))/(1+x^2 ))dx>∫_0 ^∞ ((−dx)/(1+x^2 )) since max value cos(lnx)=1 min value cos(lnx)=−1 so ∫_0 ^∞ (dx/(1+x^2 ))>I>∫_0 ^∞ ((−dx)/(1+x^2 )) ∣tan^(−1) x∣_0 ^∞ >I>(−1)∣tan^(−1) x∣_0 ^∞ (π/2)>I>((−π)/2)
$${thinking}\:{different}\:{way}… \\ $$$$\int_{\mathrm{0}} ^{\infty} \frac{{dx}}{\mathrm{1}+{x}^{\mathrm{2}} }>\int_{\mathrm{0}} ^{\infty} \frac{{cos}\left({lnx}\right)}{\mathrm{1}+{x}^{\mathrm{2}} }{dx}>\int_{\mathrm{0}} ^{\infty} \frac{−{dx}}{\mathrm{1}+{x}^{\mathrm{2}} } \\ $$$${since}\:{max}\:{value}\:{cos}\left({lnx}\right)=\mathrm{1} \\ $$$${min}\:{value}\:{cos}\left({lnx}\right)=−\mathrm{1} \\ $$$${so}\:\int_{\mathrm{0}} ^{\infty} \frac{{dx}}{\mathrm{1}+{x}^{\mathrm{2}} }>{I}>\int_{\mathrm{0}} ^{\infty} \frac{−{dx}}{\mathrm{1}+{x}^{\mathrm{2}} } \\ $$$$\mid{tan}^{−\mathrm{1}} {x}\mid_{\mathrm{0}} ^{\infty} >{I}>\left(−\mathrm{1}\right)\mid{tan}^{−\mathrm{1}} {x}\mid_{\mathrm{0}} ^{\infty} \\ $$$$\frac{\pi}{\mathrm{2}}>{I}>\frac{−\pi}{\mathrm{2}} \\ $$
Commented by tanmay.chaudhury50@gmail.com last updated on 25/Feb/19
p=∫_0 ^∞ ((cos(lnx))/(1+x^2 ))dx q=∫_0 ^∞ ((sin(lnx))/(1+x^2 ))dx p+iq=∫_0 ^∞ (e^(i(lnx)) /(1+x^2 ))dx p+iq=∫_0 ^∞ (e^(lnx^i ) /(1+x^2 ))dx→∫_0 ^∞ (x^i /(1+x^2 ))dx x=tana ∫_0 ^(π/2) (((tana)^i )/(sec^2 a))×sec^2 ada ∫_0 ^(π/2) (tana)^i da wait pls...
$${p}=\int_{\mathrm{0}} ^{\infty} \frac{{cos}\left({lnx}\right)}{\mathrm{1}+{x}^{\mathrm{2}} }{dx}\:\:\:{q}=\int_{\mathrm{0}} ^{\infty} \frac{{sin}\left({lnx}\right)}{\mathrm{1}+{x}^{\mathrm{2}} }{dx} \\ $$$${p}+{iq}=\int_{\mathrm{0}} ^{\infty} \frac{{e}^{{i}\left({lnx}\right)} }{\mathrm{1}+{x}^{\mathrm{2}} }{dx} \\ $$$${p}+{iq}=\int_{\mathrm{0}} ^{\infty} \frac{{e}^{{lnx}^{{i}} } }{\mathrm{1}+{x}^{\mathrm{2}} }{dx}\rightarrow\int_{\mathrm{0}} ^{\infty} \frac{{x}^{{i}} }{\mathrm{1}+{x}^{\mathrm{2}} }{dx} \\ $$$${x}={tana} \\ $$$$\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \frac{\left({tana}\right)^{{i}} }{{sec}^{\mathrm{2}} {a}}×{sec}^{\mathrm{2}} {ada} \\ $$$$\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \left({tana}\right)^{{i}} {da} \\ $$$${wait}\:{pls}… \\ $$$$ \\ $$
Commented by maxmathsup by imad last updated on 26/Feb/19
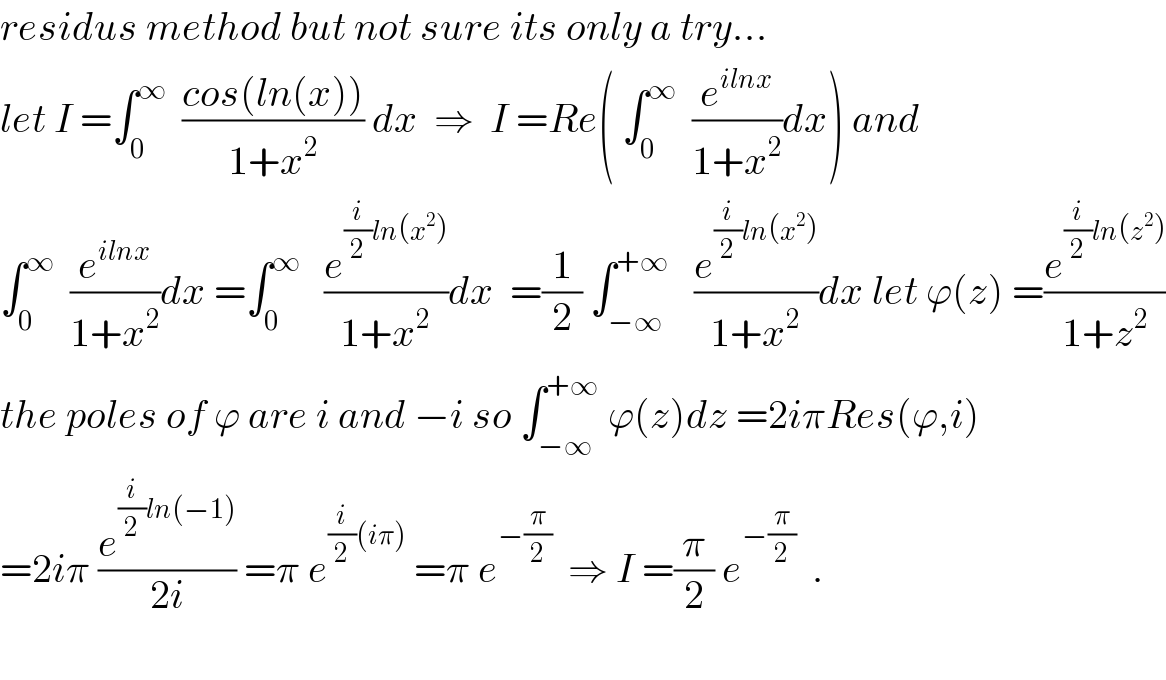
residus method but not sure its only a try... let I =∫_0 ^∞ ((cos(ln(x)))/(1+x^2 )) dx ⇒ I =Re( ∫_0 ^∞ (e^(ilnx) /(1+x^2 ))dx) and ∫_0 ^∞ (e^(ilnx) /(1+x^2 ))dx =∫_0 ^∞ (e^((i/2)ln(x^2 )) /(1+x^2 ))dx =(1/2) ∫_(−∞) ^(+∞) (e^((i/2)ln(x^2 )) /(1+x^2 ))dx let ϕ(z) =(e^((i/2)ln(z^2 )) /(1+z^2 )) the poles of ϕ are i and −i so ∫_(−∞) ^(+∞) ϕ(z)dz =2iπRes(ϕ,i) =2iπ (e^((i/2)ln(−1)) /(2i)) =π e^((i/2)(iπ)) =π e^(−(π/2)) ⇒ I =(π/2) e^(−(π/2)) .
$${residus}\:{method}\:{but}\:{not}\:{sure}\:{its}\:{only}\:{a}\:{try}… \\ $$$${let}\:{I}\:=\int_{\mathrm{0}} ^{\infty} \:\:\frac{{cos}\left({ln}\left({x}\right)\right)}{\mathrm{1}+{x}^{\mathrm{2}} }\:{dx}\:\:\Rightarrow\:\:{I}\:={Re}\left(\:\int_{\mathrm{0}} ^{\infty} \:\:\frac{{e}^{{ilnx}} }{\mathrm{1}+{x}^{\mathrm{2}} }{dx}\right)\:{and} \\ $$$$\int_{\mathrm{0}} ^{\infty} \:\:\frac{{e}^{{ilnx}} }{\mathrm{1}+{x}^{\mathrm{2}} }{dx}\:=\int_{\mathrm{0}} ^{\infty} \:\:\:\frac{{e}^{\frac{{i}}{\mathrm{2}}{ln}\left({x}^{\mathrm{2}} \right)} }{\mathrm{1}+{x}^{\mathrm{2}} }{dx}\:\:=\frac{\mathrm{1}}{\mathrm{2}}\:\int_{−\infty} ^{+\infty} \:\:\:\frac{{e}^{\frac{{i}}{\mathrm{2}}{ln}\left({x}^{\mathrm{2}} \right)} }{\mathrm{1}+{x}^{\mathrm{2}} }{dx}\:{let}\:\varphi\left({z}\right)\:=\frac{{e}^{\frac{{i}}{\mathrm{2}}{ln}\left({z}^{\mathrm{2}} \right)} }{\mathrm{1}+{z}^{\mathrm{2}} } \\ $$$${the}\:{poles}\:{of}\:\varphi\:{are}\:{i}\:{and}\:−{i}\:{so}\:\int_{−\infty} ^{+\infty} \:\varphi\left({z}\right){dz}\:=\mathrm{2}{i}\pi{Res}\left(\varphi,{i}\right) \\ $$$$=\mathrm{2}{i}\pi\:\frac{{e}^{\frac{{i}}{\mathrm{2}}{ln}\left(−\mathrm{1}\right)} }{\mathrm{2}{i}}\:=\pi\:{e}^{\frac{{i}}{\mathrm{2}}\left({i}\pi\right)} \:=\pi\:{e}^{−\frac{\pi}{\mathrm{2}}} \:\:\Rightarrow\:{I}\:=\frac{\pi}{\mathrm{2}}\:{e}^{−\frac{\pi}{\mathrm{2}}} \:\:. \\ $$$$ \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *