Question Number 121002 by Ar Brandon last updated on 04/Nov/20

Answered by MJS_new last updated on 04/Nov/20

$$ \\ $$
Commented by Ar Brandon last updated on 04/Nov/20
Alright Sir. Thanks for your attention
Commented by MJS_new last updated on 04/Nov/20
$$\mathrm{I}\:\mathrm{simply}\:\mathrm{didn}'\mathrm{t}\:\mathrm{see}\:\mathrm{it} \\ $$
Answered by 675480065 last updated on 04/Nov/20
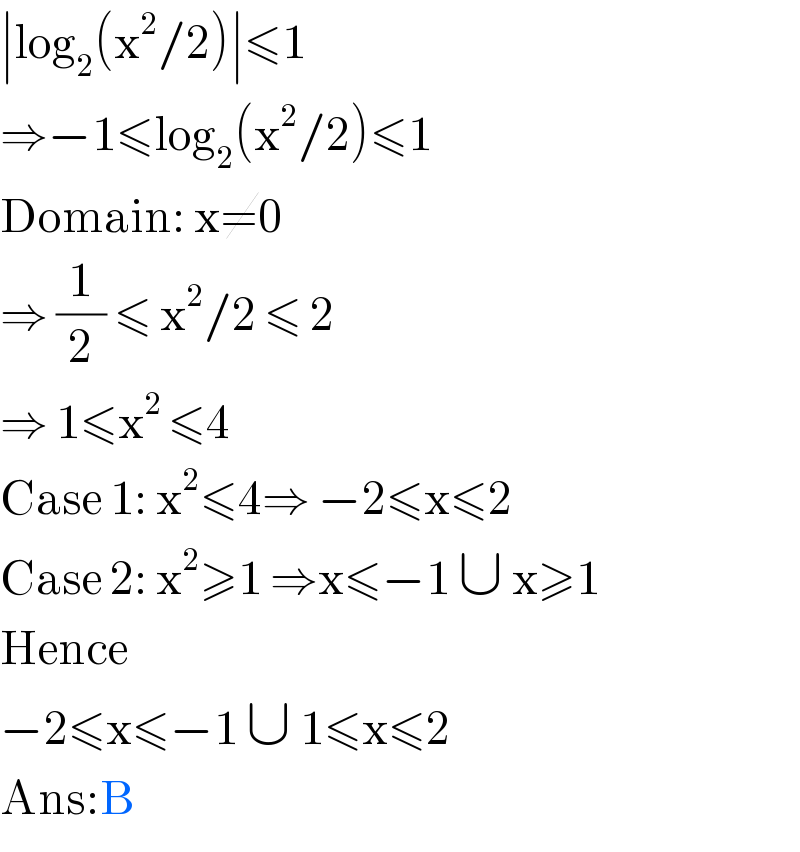
$$\mid\mathrm{log}_{\mathrm{2}} \left(\mathrm{x}^{\mathrm{2}} /\mathrm{2}\right)\mid\leqslant\mathrm{1} \\ $$$$\Rightarrow−\mathrm{1}\leqslant\mathrm{log}_{\mathrm{2}} \left(\mathrm{x}^{\mathrm{2}} /\mathrm{2}\right)\leqslant\mathrm{1} \\ $$$$\mathrm{Domain}:\:\mathrm{x}\neq\mathrm{0} \\ $$$$\Rightarrow\:\frac{\mathrm{1}}{\mathrm{2}}\:\leqslant\:\mathrm{x}^{\mathrm{2}} /\mathrm{2}\:\leqslant\:\mathrm{2} \\ $$$$\Rightarrow\:\mathrm{1}\leqslant\mathrm{x}^{\mathrm{2}\:} \leqslant\mathrm{4} \\ $$$$\mathrm{Case}\:\mathrm{1}:\:\mathrm{x}^{\mathrm{2}} \leqslant\mathrm{4}\Rightarrow\:−\mathrm{2}\leqslant\mathrm{x}\leqslant\mathrm{2} \\ $$$$\mathrm{Case}\:\mathrm{2}:\:\mathrm{x}^{\mathrm{2}} \geqslant\mathrm{1}\:\Rightarrow\mathrm{x}\leqslant−\mathrm{1}\:\cup\:\mathrm{x}\geqslant\mathrm{1} \\ $$$$\mathrm{Hence}\: \\ $$$$−\mathrm{2}\leqslant\mathrm{x}\leqslant−\mathrm{1}\:\cup\:\mathrm{1}\leqslant\mathrm{x}\leqslant\mathrm{2} \\ $$$$\mathrm{Ans}:\mathrm{B} \\ $$
Commented by MJS_new last updated on 04/Nov/20
$$\mathrm{good},\:\mathrm{I}\:\mathrm{just}\:\mathrm{was}\:\mathrm{about}\:\mathrm{to}\:\mathrm{post}\:\mathrm{the}\:\mathrm{same}… \\ $$
Commented by Ar Brandon last updated on 04/Nov/20
Thanks
Answered by mathmax by abdo last updated on 04/Nov/20
![∣log_2 ((x^2 /2))∣≤1 ⇔−1≤log_2 ((x^2 /2))≤1 ⇒−1≤((ln((x^2 /2)))/(ln2))≤1 ⇒ −ln2 ≤ln((x^2 /2))≤ln2 ⇒(1/2)≤(x^2 /2)≤2 ⇒1≤x^2 ≤4 ⇒1≤(√x^2 )≤2 ⇒ 1≤∣x∣≤2⇒x∈[−2,−1]∪[1,2]](https://www.tinkutara.com/question/Q121023.png)
$$\mid\mathrm{log}_{\mathrm{2}} \left(\frac{\mathrm{x}^{\mathrm{2}} }{\mathrm{2}}\right)\mid\leqslant\mathrm{1}\:\Leftrightarrow−\mathrm{1}\leqslant\mathrm{log}_{\mathrm{2}} \left(\frac{\mathrm{x}^{\mathrm{2}} }{\mathrm{2}}\right)\leqslant\mathrm{1}\:\Rightarrow−\mathrm{1}\leqslant\frac{\mathrm{ln}\left(\frac{\mathrm{x}^{\mathrm{2}} }{\mathrm{2}}\right)}{\mathrm{ln2}}\leqslant\mathrm{1}\:\Rightarrow \\ $$$$−\mathrm{ln2}\:\leqslant\mathrm{ln}\left(\frac{\mathrm{x}^{\mathrm{2}} }{\mathrm{2}}\right)\leqslant\mathrm{ln2}\:\Rightarrow\frac{\mathrm{1}}{\mathrm{2}}\leqslant\frac{\mathrm{x}^{\mathrm{2}} }{\mathrm{2}}\leqslant\mathrm{2}\:\Rightarrow\mathrm{1}\leqslant\mathrm{x}^{\mathrm{2}} \leqslant\mathrm{4}\:\Rightarrow\mathrm{1}\leqslant\sqrt{\mathrm{x}^{\mathrm{2}} }\leqslant\mathrm{2}\:\Rightarrow \\ $$$$\mathrm{1}\leqslant\mid\mathrm{x}\mid\leqslant\mathrm{2}\Rightarrow\mathrm{x}\in\left[−\mathrm{2},−\mathrm{1}\right]\cup\left[\mathrm{1},\mathrm{2}\right] \\ $$
