Question Number 186752 by depressiveshrek last updated on 09/Feb/23
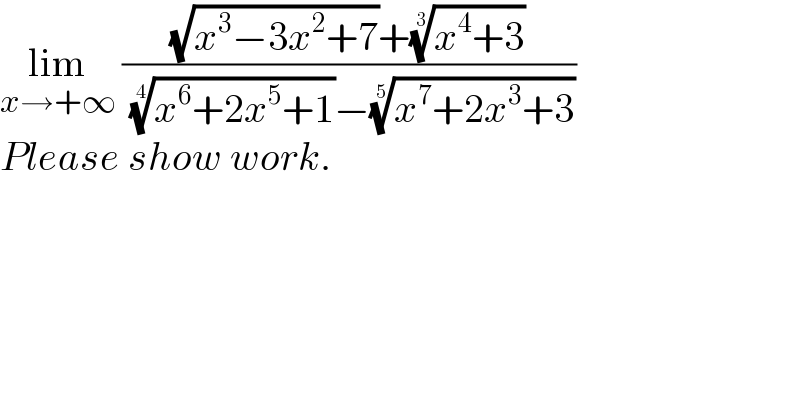
$$\underset{{x}\rightarrow+\infty} {\mathrm{lim}}\:\frac{\sqrt{{x}^{\mathrm{3}} −\mathrm{3}{x}^{\mathrm{2}} +\mathrm{7}}+\sqrt[{\mathrm{3}}]{{x}^{\mathrm{4}} +\mathrm{3}}}{\:\sqrt[{\mathrm{4}}]{{x}^{\mathrm{6}} +\mathrm{2}{x}^{\mathrm{5}} +\mathrm{1}}−\sqrt[{\mathrm{5}}]{{x}^{\mathrm{7}} +\mathrm{2}{x}^{\mathrm{3}} +\mathrm{3}}} \\ $$$${Please}\:{show}\:{work}. \\ $$
Answered by Ar Brandon last updated on 09/Feb/23
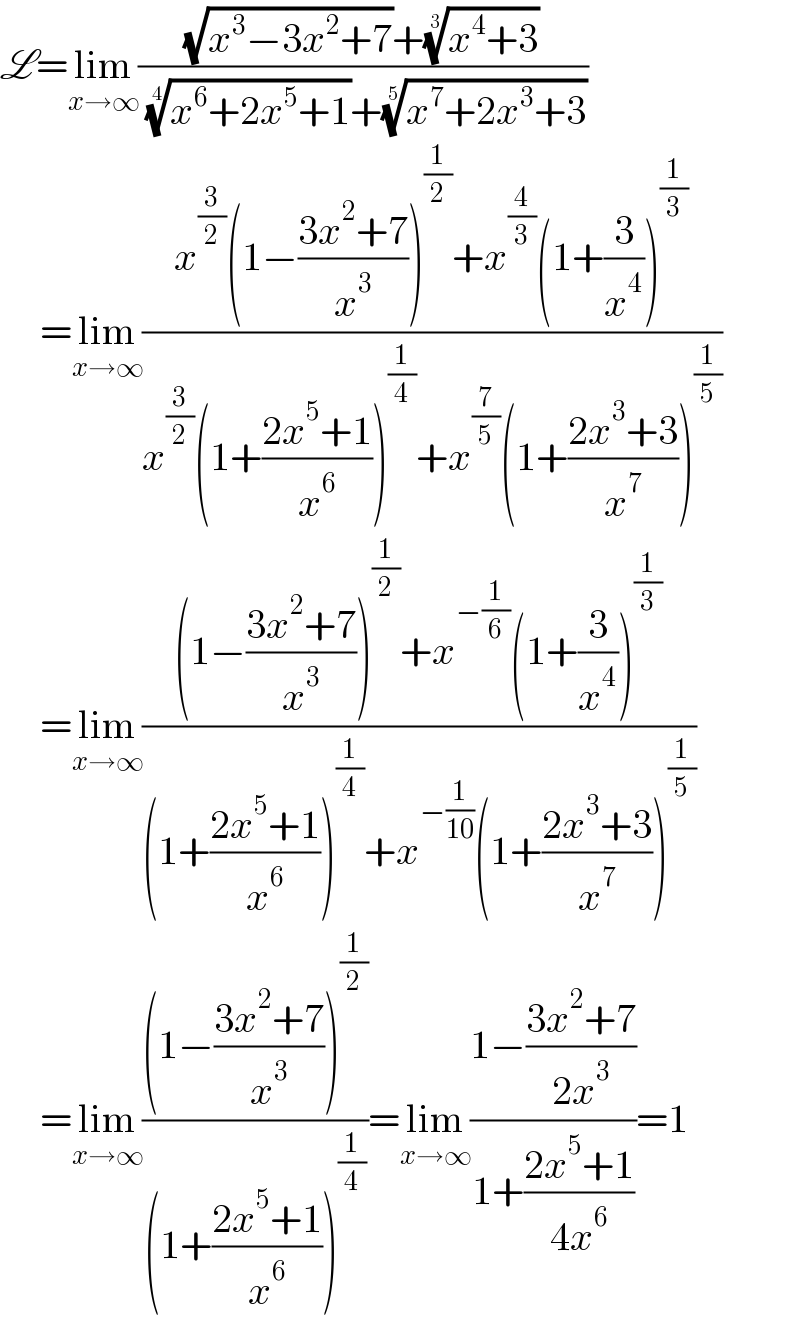
$$\mathscr{L}=\underset{{x}\rightarrow\infty} {\mathrm{lim}}\frac{\sqrt{{x}^{\mathrm{3}} −\mathrm{3}{x}^{\mathrm{2}} +\mathrm{7}}+\sqrt[{\mathrm{3}}]{{x}^{\mathrm{4}} +\mathrm{3}}}{\:\sqrt[{\mathrm{4}}]{{x}^{\mathrm{6}} +\mathrm{2}{x}^{\mathrm{5}} +\mathrm{1}}+\sqrt[{\mathrm{5}}]{{x}^{\mathrm{7}} +\mathrm{2}{x}^{\mathrm{3}} +\mathrm{3}}} \\ $$$$\:\:\:\:\:=\underset{{x}\rightarrow\infty} {\mathrm{lim}}\frac{{x}^{\frac{\mathrm{3}}{\mathrm{2}}} \left(\mathrm{1}−\frac{\mathrm{3}{x}^{\mathrm{2}} +\mathrm{7}}{{x}^{\mathrm{3}} }\right)^{\frac{\mathrm{1}}{\mathrm{2}}} +{x}^{\frac{\mathrm{4}}{\mathrm{3}}} \left(\mathrm{1}+\frac{\mathrm{3}}{{x}^{\mathrm{4}} }\right)^{\frac{\mathrm{1}}{\mathrm{3}}} }{{x}^{\frac{\mathrm{3}}{\mathrm{2}}} \left(\mathrm{1}+\frac{\mathrm{2}{x}^{\mathrm{5}} +\mathrm{1}}{{x}^{\mathrm{6}} }\right)^{\frac{\mathrm{1}}{\mathrm{4}}} +{x}^{\frac{\mathrm{7}}{\mathrm{5}}} \left(\mathrm{1}+\frac{\mathrm{2}{x}^{\mathrm{3}} +\mathrm{3}}{{x}^{\mathrm{7}} }\right)^{\frac{\mathrm{1}}{\mathrm{5}}} } \\ $$$$\:\:\:\:\:=\underset{{x}\rightarrow\infty} {\mathrm{lim}}\frac{\left(\mathrm{1}−\frac{\mathrm{3}{x}^{\mathrm{2}} +\mathrm{7}}{{x}^{\mathrm{3}} }\right)^{\frac{\mathrm{1}}{\mathrm{2}}} +{x}^{−\frac{\mathrm{1}}{\mathrm{6}}} \left(\mathrm{1}+\frac{\mathrm{3}}{{x}^{\mathrm{4}} }\right)^{\frac{\mathrm{1}}{\mathrm{3}}} }{\left(\mathrm{1}+\frac{\mathrm{2}{x}^{\mathrm{5}} +\mathrm{1}}{{x}^{\mathrm{6}} }\right)^{\frac{\mathrm{1}}{\mathrm{4}}} +{x}^{−\frac{\mathrm{1}}{\mathrm{10}}} \left(\mathrm{1}+\frac{\mathrm{2}{x}^{\mathrm{3}} +\mathrm{3}}{{x}^{\mathrm{7}} }\right)^{\frac{\mathrm{1}}{\mathrm{5}}} } \\ $$$$\:\:\:\:\:=\underset{{x}\rightarrow\infty} {\mathrm{lim}}\frac{\left(\mathrm{1}−\frac{\mathrm{3}{x}^{\mathrm{2}} +\mathrm{7}}{{x}^{\mathrm{3}} }\right)^{\frac{\mathrm{1}}{\mathrm{2}}} }{\left(\mathrm{1}+\frac{\mathrm{2}{x}^{\mathrm{5}} +\mathrm{1}}{{x}^{\mathrm{6}} }\right)^{\frac{\mathrm{1}}{\mathrm{4}}} }=\underset{{x}\rightarrow\infty} {\mathrm{lim}}\frac{\mathrm{1}−\frac{\mathrm{3}{x}^{\mathrm{2}} +\mathrm{7}}{\mathrm{2}{x}^{\mathrm{3}} }}{\mathrm{1}+\frac{\mathrm{2}{x}^{\mathrm{5}} +\mathrm{1}}{\mathrm{4}{x}^{\mathrm{6}} }}=\mathrm{1} \\ $$
