Question Number 131517 by benjo_mathlover last updated on 05/Feb/21
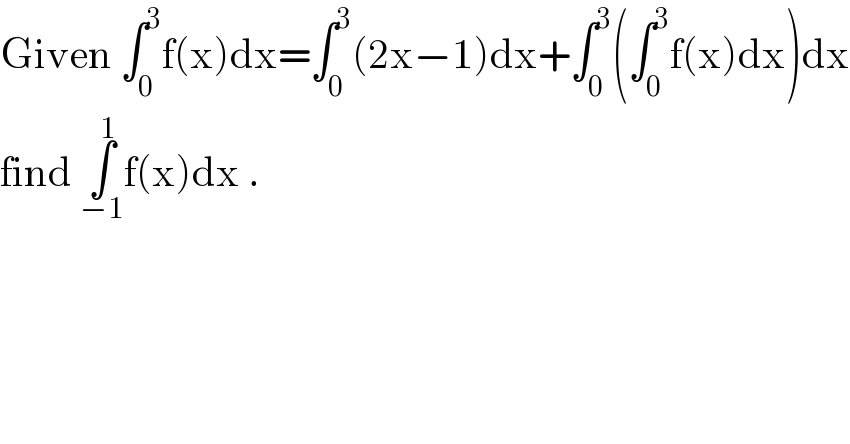
$$\mathrm{Given}\:\int_{\mathrm{0}} ^{\mathrm{3}} \mathrm{f}\left(\mathrm{x}\right)\mathrm{dx}=\int_{\mathrm{0}} ^{\mathrm{3}} \left(\mathrm{2x}−\mathrm{1}\right)\mathrm{dx}+\int_{\mathrm{0}} ^{\mathrm{3}} \left(\int_{\mathrm{0}} ^{\mathrm{3}} \mathrm{f}\left(\mathrm{x}\right)\mathrm{dx}\right)\mathrm{dx} \\ $$$$\mathrm{find}\:\underset{−\mathrm{1}} {\overset{\mathrm{1}} {\int}}\mathrm{f}\left(\mathrm{x}\right)\mathrm{dx}\:. \\ $$
Answered by EDWIN88 last updated on 05/Feb/21
![let ∫_0 ^3 f(x)dx =ℓ ⇒ℓ=[ x^2 −x]_0 ^3 + ∫_0 ^3 ℓ dx ℓ = 6+3ℓ ; ℓ = −3 or ∫_0 ^3 f(x)dx =−3 then −3 = ∫_0 ^3 (2x−1)dx+∫_0 ^3 −3dx ⇒ −3 = ∫_0 ^3 (2x−4)dx ⇒∫_0 ^3 f(x)dx =∫_0 ^3 (2x−4)dx by theorem ∫_a ^b f(x)dx=∫_a ^b f(a+b−x)dx we have ∫_0 ^3 f(x)dx=∫_0 ^3 f(3−x)dx ; so f(3−x) = 2x−4 or f(x)=2(3−x)−4=2−2x Now ∫_(−1) ^1 f(x)dx = ∫_(−1) ^1 (2−2x)dx=[ 2x−x^2 ]_(−1) ^1 = (1)−(−3)= 4. check if f(x)=2−2x ⇒∫_0 ^3 f(x)dx=∫_0 ^3 (2−2x)dx = [ 2x−x^2 ]_0 ^3 = 6−9=−3 (true)](https://www.tinkutara.com/question/Q131518.png)
$$\mathrm{let}\:\underset{\mathrm{0}} {\overset{\mathrm{3}} {\int}}\mathrm{f}\left(\mathrm{x}\right)\mathrm{dx}\:=\ell\:\Rightarrow\ell=\left[\:\mathrm{x}^{\mathrm{2}} −\mathrm{x}\right]_{\mathrm{0}} ^{\mathrm{3}} \:+\:\int_{\mathrm{0}} ^{\mathrm{3}} \ell\:\mathrm{dx} \\ $$$$\ell\:=\:\mathrm{6}+\mathrm{3}\ell\:;\:\ell\:=\:−\mathrm{3}\:\mathrm{or}\:\underset{\mathrm{0}} {\overset{\mathrm{3}} {\int}}\mathrm{f}\left(\mathrm{x}\right)\mathrm{dx}\:=−\mathrm{3} \\ $$$$\mathrm{then}\:−\mathrm{3}\:=\:\underset{\mathrm{0}} {\overset{\mathrm{3}} {\int}}\left(\mathrm{2x}−\mathrm{1}\right)\mathrm{dx}+\underset{\mathrm{0}} {\overset{\mathrm{3}} {\int}}−\mathrm{3dx} \\ $$$$\Rightarrow\:−\mathrm{3}\:=\:\underset{\mathrm{0}} {\overset{\mathrm{3}} {\int}}\left(\mathrm{2x}−\mathrm{4}\right)\mathrm{dx}\:\Rightarrow\underset{\mathrm{0}} {\overset{\mathrm{3}} {\int}}\mathrm{f}\left(\mathrm{x}\right)\mathrm{dx}\:=\underset{\mathrm{0}} {\overset{\mathrm{3}} {\int}}\left(\mathrm{2x}−\mathrm{4}\right)\mathrm{dx} \\ $$$$\mathrm{by}\:\mathrm{theorem}\:\underset{\mathrm{a}} {\overset{\mathrm{b}} {\int}}\mathrm{f}\left(\mathrm{x}\right)\mathrm{dx}=\underset{\mathrm{a}} {\overset{\mathrm{b}} {\int}}\mathrm{f}\left(\mathrm{a}+\mathrm{b}−\mathrm{x}\right)\mathrm{dx} \\ $$$$\mathrm{we}\:\mathrm{have}\:\underset{\mathrm{0}} {\overset{\mathrm{3}} {\int}}\mathrm{f}\left(\mathrm{x}\right)\mathrm{dx}=\underset{\mathrm{0}} {\overset{\mathrm{3}} {\int}}\mathrm{f}\left(\mathrm{3}−\mathrm{x}\right)\mathrm{dx}\:;\:\mathrm{so}\: \\ $$$$\mathrm{f}\left(\mathrm{3}−\mathrm{x}\right)\:=\:\mathrm{2x}−\mathrm{4}\:\mathrm{or}\:\mathrm{f}\left(\mathrm{x}\right)=\mathrm{2}\left(\mathrm{3}−\mathrm{x}\right)−\mathrm{4}=\mathrm{2}−\mathrm{2x} \\ $$$$\mathrm{Now}\:\underset{−\mathrm{1}} {\overset{\mathrm{1}} {\int}}\mathrm{f}\left(\mathrm{x}\right)\mathrm{dx}\:=\:\underset{−\mathrm{1}} {\overset{\mathrm{1}} {\int}}\left(\mathrm{2}−\mathrm{2x}\right)\mathrm{dx}=\left[\:\mathrm{2x}−\mathrm{x}^{\mathrm{2}} \:\right]_{−\mathrm{1}} ^{\mathrm{1}} \\ $$$$=\:\left(\mathrm{1}\right)−\left(−\mathrm{3}\right)=\:\mathrm{4}. \\ $$$$\mathrm{check}\:\mathrm{if}\:\mathrm{f}\left(\mathrm{x}\right)=\mathrm{2}−\mathrm{2x}\:\Rightarrow\underset{\mathrm{0}} {\overset{\mathrm{3}} {\int}}\mathrm{f}\left(\mathrm{x}\right)\mathrm{dx}=\underset{\mathrm{0}} {\overset{\mathrm{3}} {\int}}\left(\mathrm{2}−\mathrm{2x}\right)\mathrm{dx} \\ $$$$\:=\:\left[\:\mathrm{2x}−\mathrm{x}^{\mathrm{2}} \right]_{\mathrm{0}} ^{\mathrm{3}} \:=\:\mathrm{6}−\mathrm{9}=−\mathrm{3}\:\left(\mathrm{true}\right)\: \\ $$
