Question Number 55815 by Rio Mike last updated on 04/Mar/19
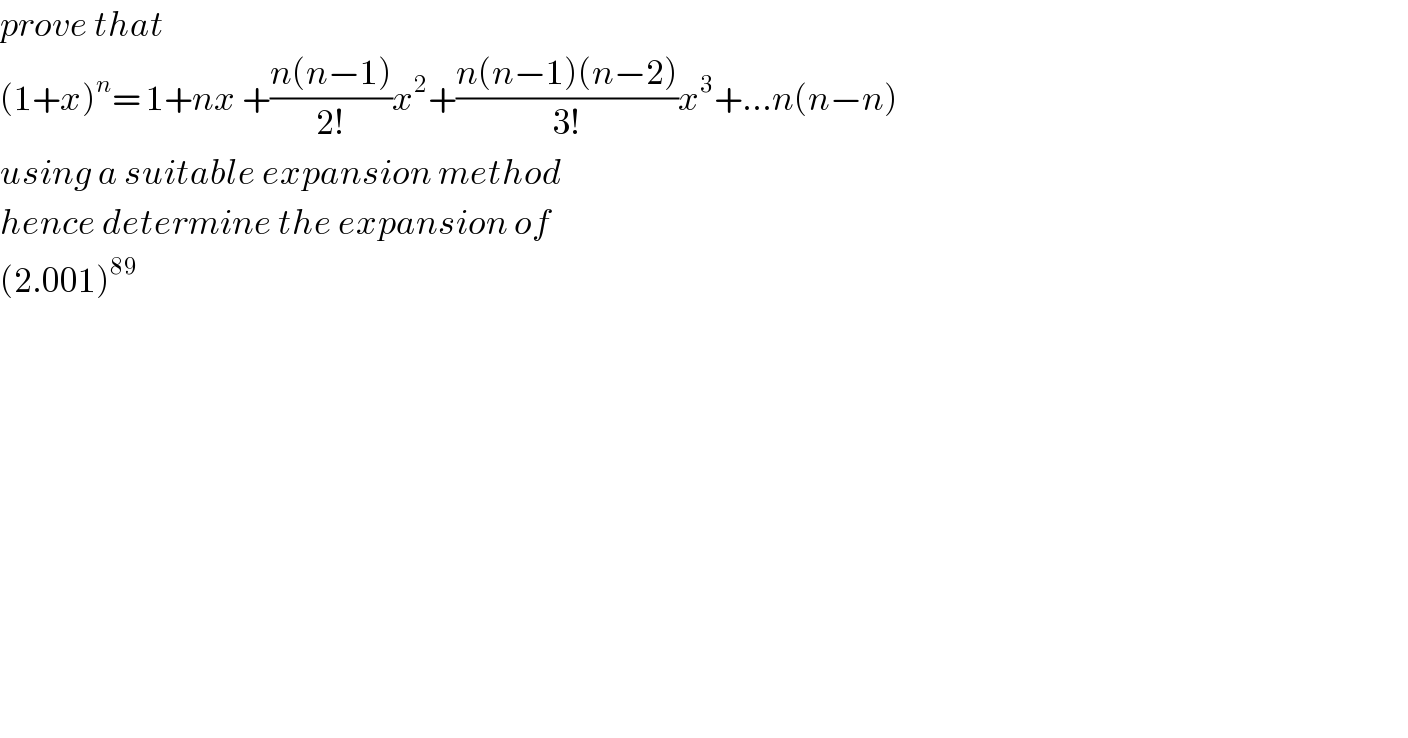
$${prove}\:{that} \\ $$$$\left(\mathrm{1}+{x}\right)^{{n}} =\:\mathrm{1}+{nx}\:+\frac{{n}\left({n}−\mathrm{1}\right)}{\mathrm{2}!}{x}^{\mathrm{2}} +\frac{{n}\left({n}−\mathrm{1}\right)\left({n}−\mathrm{2}\right)}{\mathrm{3}!}{x}^{\mathrm{3}} +…{n}\left({n}−{n}\right) \\ $$$${using}\:{a}\:{suitable}\:{expansion}\:{method} \\ $$$${hence}\:{determine}\:{the}\:{expansion}\:{of} \\ $$$$\left(\mathrm{2}.\mathrm{001}\right)^{\mathrm{89}} \\ $$$$ \\ $$$$ \\ $$$$ \\ $$$$ \\ $$$$ \\ $$$$ \\ $$$$ \\ $$$$ \\ $$
Answered by Kunal12588 last updated on 04/Mar/19
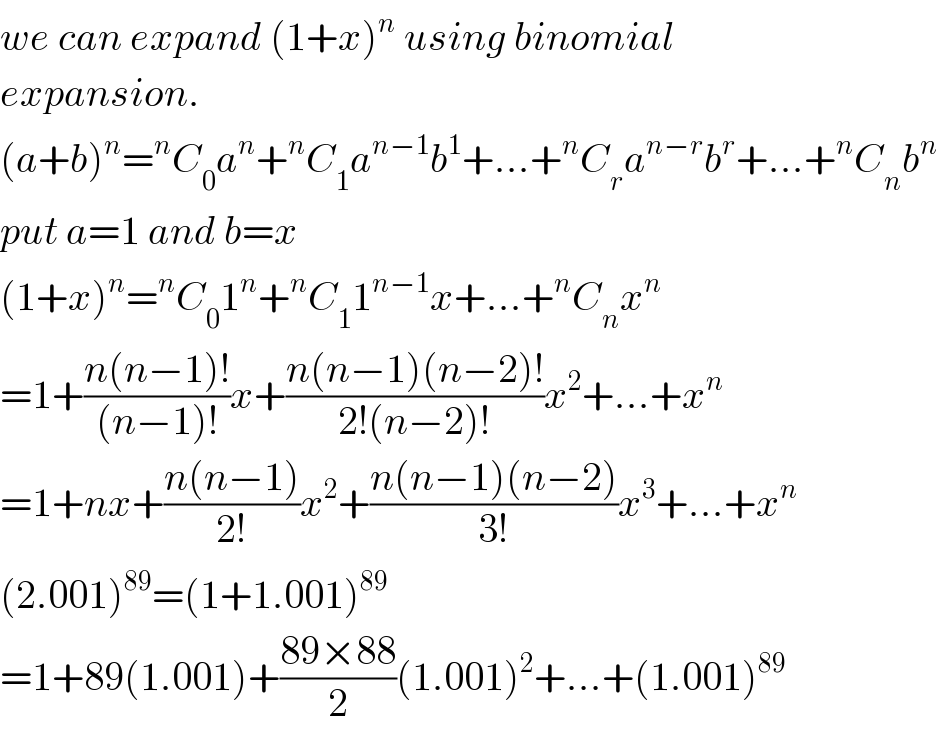
$${we}\:{can}\:{expand}\:\left(\mathrm{1}+{x}\right)^{{n}} \:{using}\:{binomial} \\ $$$${expansion}. \\ $$$$\left({a}+{b}\right)^{{n}} =^{{n}} {C}_{\mathrm{0}} {a}^{{n}} +^{{n}} {C}_{\mathrm{1}} {a}^{{n}−\mathrm{1}} {b}^{\mathrm{1}} +…+^{{n}} {C}_{{r}} {a}^{{n}−{r}} {b}^{{r}} +…+^{{n}} {C}_{{n}} {b}^{{n}} \\ $$$${put}\:{a}=\mathrm{1}\:{and}\:{b}={x} \\ $$$$\left(\mathrm{1}+{x}\right)^{{n}} =^{{n}} {C}_{\mathrm{0}} \mathrm{1}^{{n}} +^{{n}} {C}_{\mathrm{1}} \mathrm{1}^{{n}−\mathrm{1}} {x}+…+^{{n}} {C}_{{n}} {x}^{{n}} \\ $$$$=\mathrm{1}+\frac{{n}\left({n}−\mathrm{1}\right)!}{\left({n}−\mathrm{1}\right)!}{x}+\frac{{n}\left({n}−\mathrm{1}\right)\left({n}−\mathrm{2}\right)!}{\mathrm{2}!\left({n}−\mathrm{2}\right)!}{x}^{\mathrm{2}} +…+{x}^{{n}} \\ $$$$=\mathrm{1}+{nx}+\frac{{n}\left({n}−\mathrm{1}\right)}{\mathrm{2}!}{x}^{\mathrm{2}} +\frac{{n}\left({n}−\mathrm{1}\right)\left({n}−\mathrm{2}\right)}{\mathrm{3}!}{x}^{\mathrm{3}} +…+{x}^{{n}} \\ $$$$\left(\mathrm{2}.\mathrm{001}\right)^{\mathrm{89}} =\left(\mathrm{1}+\mathrm{1}.\mathrm{001}\right)^{\mathrm{89}} \\ $$$$=\mathrm{1}+\mathrm{89}\left(\mathrm{1}.\mathrm{001}\right)+\frac{\mathrm{89}×\mathrm{88}}{\mathrm{2}}\left(\mathrm{1}.\mathrm{001}\right)^{\mathrm{2}} +…+\left(\mathrm{1}.\mathrm{001}\right)^{\mathrm{89}} \\ $$
