Question Number 55902 by naka3546 last updated on 06/Mar/19

Answered by MJS last updated on 06/Mar/19
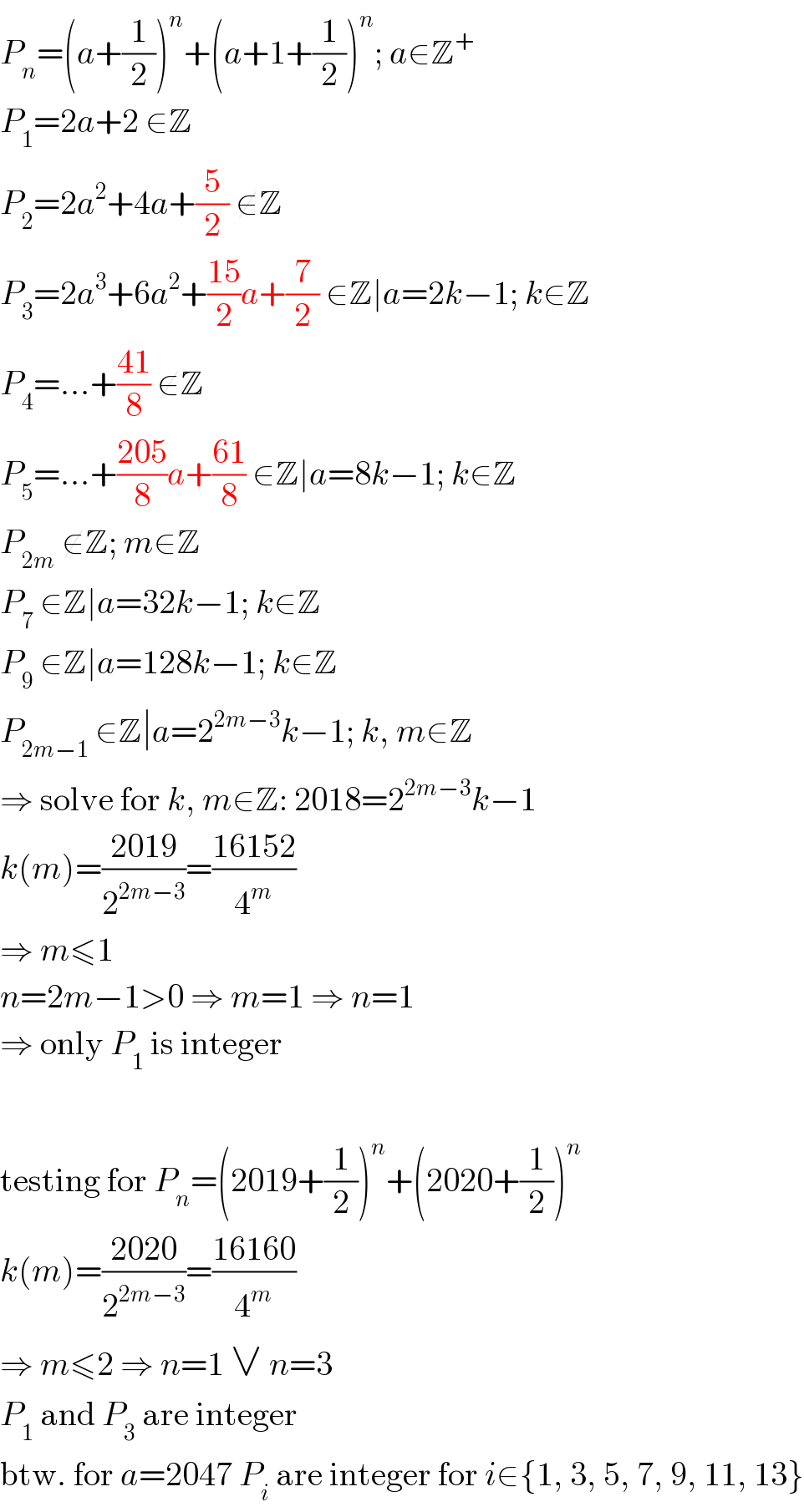
$${P}_{{n}} =\left({a}+\frac{\mathrm{1}}{\mathrm{2}}\right)^{{n}} +\left({a}+\mathrm{1}+\frac{\mathrm{1}}{\mathrm{2}}\right)^{{n}} ;\:{a}\in\mathbb{Z}^{+} \\ $$$${P}_{\mathrm{1}} =\mathrm{2}{a}+\mathrm{2}\:\in\mathbb{Z} \\ $$$${P}_{\mathrm{2}} =\mathrm{2}{a}^{\mathrm{2}} +\mathrm{4}{a}+\frac{\mathrm{5}}{\mathrm{2}}\:\notin\mathbb{Z} \\ $$$${P}_{\mathrm{3}} =\mathrm{2}{a}^{\mathrm{3}} +\mathrm{6}{a}^{\mathrm{2}} +\frac{\mathrm{15}}{\mathrm{2}}{a}+\frac{\mathrm{7}}{\mathrm{2}}\:\in\mathbb{Z}\mid{a}=\mathrm{2}{k}−\mathrm{1};\:{k}\in\mathbb{Z} \\ $$$${P}_{\mathrm{4}} =…+\frac{\mathrm{41}}{\mathrm{8}}\:\notin\mathbb{Z} \\ $$$${P}_{\mathrm{5}} =…+\frac{\mathrm{205}}{\mathrm{8}}{a}+\frac{\mathrm{61}}{\mathrm{8}}\:\in\mathbb{Z}\mid{a}=\mathrm{8}{k}−\mathrm{1};\:{k}\in\mathbb{Z} \\ $$$${P}_{\mathrm{2}{m}} \:\notin\mathbb{Z};\:{m}\in\mathbb{Z} \\ $$$${P}_{\mathrm{7}} \:\in\mathbb{Z}\mid{a}=\mathrm{32}{k}−\mathrm{1};\:{k}\in\mathbb{Z} \\ $$$${P}_{\mathrm{9}} \:\in\mathbb{Z}\mid{a}=\mathrm{128}{k}−\mathrm{1};\:{k}\in\mathbb{Z} \\ $$$${P}_{\mathrm{2}{m}−\mathrm{1}} \:\in\mathbb{Z}\mid{a}=\mathrm{2}^{\mathrm{2}{m}−\mathrm{3}} {k}−\mathrm{1};\:{k},\:{m}\in\mathbb{Z} \\ $$$$\Rightarrow\:\mathrm{solve}\:\mathrm{for}\:{k},\:{m}\in\mathbb{Z}:\:\mathrm{2018}=\mathrm{2}^{\mathrm{2}{m}−\mathrm{3}} {k}−\mathrm{1} \\ $$$${k}\left({m}\right)=\frac{\mathrm{2019}}{\mathrm{2}^{\mathrm{2}{m}−\mathrm{3}} }=\frac{\mathrm{16152}}{\mathrm{4}^{{m}} } \\ $$$$\Rightarrow\:{m}\leqslant\mathrm{1} \\ $$$${n}=\mathrm{2}{m}−\mathrm{1}>\mathrm{0}\:\Rightarrow\:{m}=\mathrm{1}\:\Rightarrow\:{n}=\mathrm{1} \\ $$$$\Rightarrow\:\mathrm{only}\:{P}_{\mathrm{1}} \:\mathrm{is}\:\mathrm{integer} \\ $$$$ \\ $$$$\mathrm{testing}\:\mathrm{for}\:{P}_{{n}} =\left(\mathrm{2019}+\frac{\mathrm{1}}{\mathrm{2}}\right)^{{n}} +\left(\mathrm{2020}+\frac{\mathrm{1}}{\mathrm{2}}\right)^{{n}} \\ $$$${k}\left({m}\right)=\frac{\mathrm{2020}}{\mathrm{2}^{\mathrm{2}{m}−\mathrm{3}} }=\frac{\mathrm{16160}}{\mathrm{4}^{{m}} } \\ $$$$\Rightarrow\:{m}\leqslant\mathrm{2}\:\Rightarrow\:{n}=\mathrm{1}\:\vee\:{n}=\mathrm{3} \\ $$$${P}_{\mathrm{1}} \:\mathrm{and}\:{P}_{\mathrm{3}} \:\mathrm{are}\:\mathrm{integer} \\ $$$$\mathrm{btw}.\:\mathrm{for}\:{a}=\mathrm{2047}\:{P}_{{i}} \:\mathrm{are}\:\mathrm{integer}\:\mathrm{for}\:{i}\in\left\{\mathrm{1},\:\mathrm{3},\:\mathrm{5},\:\mathrm{7},\:\mathrm{9},\:\mathrm{11},\:\mathrm{13}\right\} \\ $$
