Question Number 121490 by mathmax by abdo last updated on 08/Nov/20
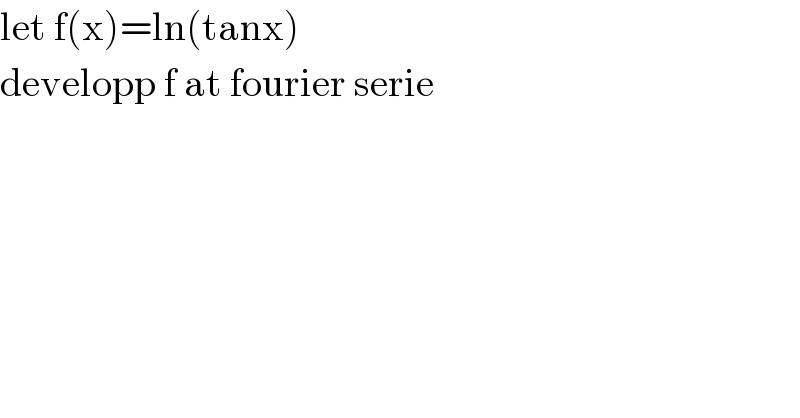
$$\mathrm{let}\:\mathrm{f}\left(\mathrm{x}\right)=\mathrm{ln}\left(\mathrm{tanx}\right) \\ $$$$\mathrm{developp}\:\mathrm{f}\:\mathrm{at}\:\mathrm{fourier}\:\mathrm{serie} \\ $$
Answered by mnjuly1970 last updated on 08/Nov/20
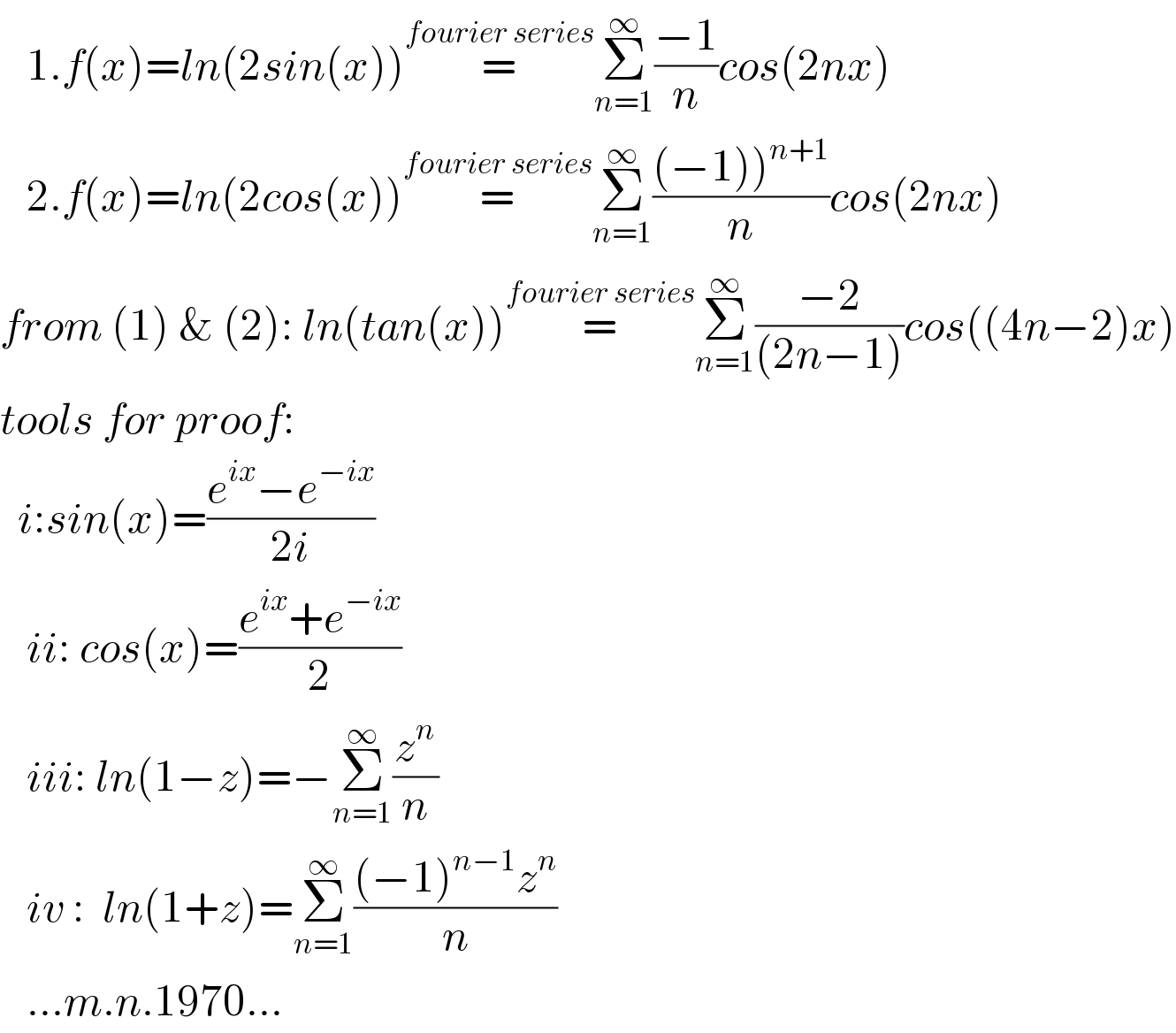
$$\:\:\:\mathrm{1}.{f}\left({x}\right)={ln}\left(\mathrm{2}{sin}\left({x}\right)\right)\overset{{fourier}\:{series}} {=}\underset{{n}=\mathrm{1}} {\overset{\infty} {\sum}}\frac{−\mathrm{1}}{{n}}{cos}\left(\mathrm{2}{nx}\right) \\ $$$$\:\:\:\mathrm{2}.{f}\left({x}\right)={ln}\left(\mathrm{2}{cos}\left({x}\right)\right)\overset{{fourier}\:{series}} {=}\underset{{n}=\mathrm{1}} {\overset{\infty} {\sum}}\frac{\left.\left(−\mathrm{1}\right)\right)^{{n}+\mathrm{1}} }{{n}}{cos}\left(\mathrm{2}{nx}\right) \\ $$$${from}\:\left(\mathrm{1}\right)\:\&\:\left(\mathrm{2}\right):\:{ln}\left({tan}\left({x}\right)\right)\overset{{fourier}\:{series}} {=}\underset{{n}=\mathrm{1}} {\overset{\infty} {\sum}}\frac{−\mathrm{2}}{\left(\mathrm{2}{n}−\mathrm{1}\right)}{cos}\left(\left(\mathrm{4}{n}−\mathrm{2}\right){x}\right) \\ $$$${tools}\:{for}\:{proof}: \\ $$$$\:\:{i}:{sin}\left({x}\right)=\frac{{e}^{{ix}} −{e}^{−{ix}} }{\mathrm{2}{i}}\: \\ $$$$\:\:\:{ii}:\:{cos}\left({x}\right)=\frac{{e}^{{ix}} +{e}^{−{ix}} }{\mathrm{2}} \\ $$$$\:\:\:{iii}:\:{ln}\left(\mathrm{1}−{z}\right)=−\underset{{n}=\mathrm{1}} {\overset{\infty} {\sum}}\frac{{z}^{{n}} }{{n}} \\ $$$$\:\:\:{iv}\::\:\:{ln}\left(\mathrm{1}+{z}\right)=\underset{{n}=\mathrm{1}} {\overset{\infty} {\sum}}\frac{\left(−\mathrm{1}\right)^{{n}−\mathrm{1}} {z}^{{n}} }{{n}} \\ $$$$\:\:\:…{m}.{n}.\mathrm{1970}… \\ $$
