Question Number 56169 by MJS last updated on 11/Mar/19
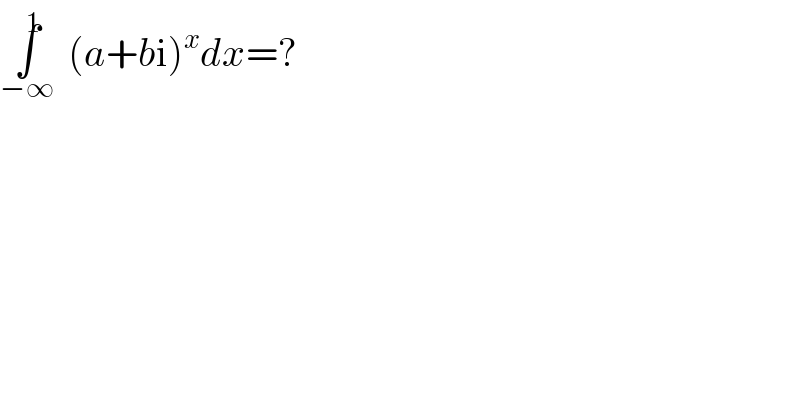
$$\underset{−\infty} {\int}^{\mathrm{1}} \left({a}+{b}\mathrm{i}\right)^{{x}} {dx}=? \\ $$
Answered by tanmay.chaudhury50@gmail.com last updated on 11/Mar/19
![∫p^x dx=(p^x /(lnp))+c but log_e (a+ib)=(1/2)log(a^2 +b^2 )+i(2nπ+tan^(−1) (b/a)) so ∣(a+ib)^x ∣_(−∞) ^1 /[(1/2)log_e (a^2 +b^2 )+i(2nπ+tan^(−1) (b/a))] (a+ib)/[(1/(2l))log_e (a^2 +b^2 )+i(2nπ+tan^(−1) (b/a)) i have rectified...](https://www.tinkutara.com/question/Q56176.png)
$$\int{p}^{{x}} {dx}=\frac{{p}^{{x}} }{{lnp}}+{c} \\ $$$${but}\:{log}_{{e}} \left({a}+{ib}\right)=\frac{\mathrm{1}}{\mathrm{2}}{log}\left({a}^{\mathrm{2}} +{b}^{\mathrm{2}} \right)+{i}\left(\mathrm{2}{n}\pi+{tan}^{−\mathrm{1}} \frac{{b}}{{a}}\right) \\ $$$${so} \\ $$$$\mid\left({a}+{ib}\right)^{{x}} \mid_{−\infty} ^{\mathrm{1}} /\left[\frac{\mathrm{1}}{\mathrm{2}}{log}_{{e}} \left({a}^{\mathrm{2}} +{b}^{\mathrm{2}} \right)+{i}\left(\mathrm{2}{n}\pi+{tan}^{−\mathrm{1}} \frac{{b}}{{a}}\right)\right] \\ $$$$\left({a}+{ib}\right)/\left[\frac{\mathrm{1}}{\mathrm{2}{l}}{log}_{{e}} \left({a}^{\mathrm{2}} +{b}^{\mathrm{2}} \right)+{i}\left(\mathrm{2}{n}\pi+{tan}^{−\mathrm{1}} \frac{{b}}{{a}}\right)\right. \\ $$$${i}\:{have}\:{rectified}… \\ $$
Commented by Smail last updated on 11/Mar/19
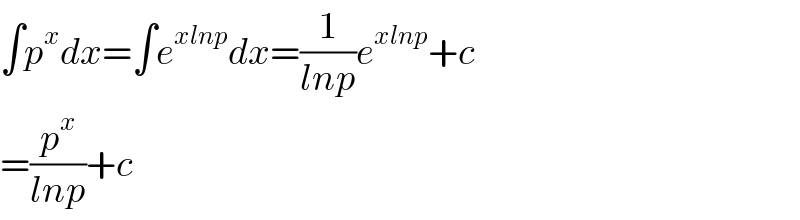
$$\int{p}^{{x}} {dx}=\int{e}^{{xlnp}} {dx}=\frac{\mathrm{1}}{{lnp}}{e}^{{xlnp}} +{c} \\ $$$$=\frac{{p}^{{x}} }{{lnp}}+{c}\:\: \\ $$
Commented by tanmay.chaudhury50@gmail.com last updated on 11/Mar/19
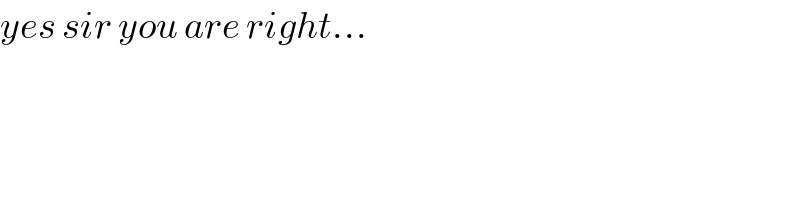
$${yes}\:{sir}\:{you}\:{are}\:{right}… \\ $$
Commented by MJS last updated on 11/Mar/19

$$\mathrm{thank}\:\mathrm{you} \\ $$
