Menu Close

Is-a-complex-number-If-not-so-what-is-It-

Tinku Tara 0 Comments
Pin




Question Number 56244 by Kunal12588 last updated on 12/Mar/19
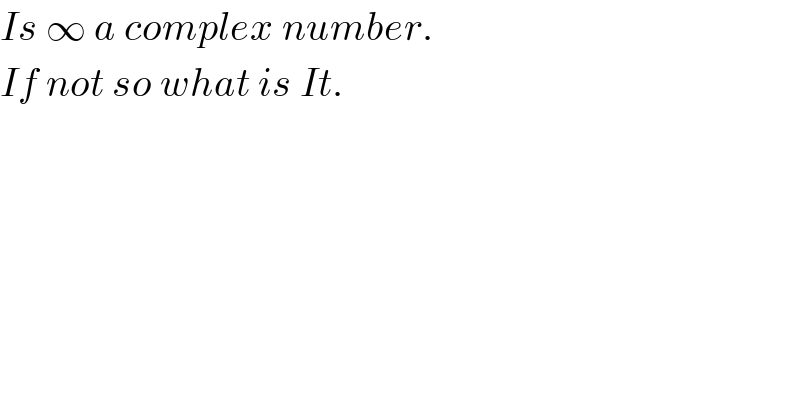
Is ∞ a complex number. If not so what is It.
$${Is}\:\infty\:{a}\:{complex}\:{number}. \\ $$$${If}\:{not}\:{so}\:{what}\:{is}\:{It}. \\ $$
Commented by Joel578 last updated on 12/Mar/19
it is not a number
$${it}\:{is}\:{not}\:{a}\:{number} \\ $$
Commented by Kunal12588 last updated on 12/Mar/19
okie dokie. waiting for then what it is and i thought we can represent it as (1/0). so (1/0) is not a number. but both numerator and denominator are numbers.
$${okie}\:{dokie}. \\ $$$${waiting}\:{for}\:{then}\:{what}\:{it}\:{is} \\ $$$${and}\:{i}\:{thought}\:{we}\:{can}\:{represent}\:{it}\:{as}\:\frac{\mathrm{1}}{\mathrm{0}}. \\ $$$${so}\:\frac{\mathrm{1}}{\mathrm{0}}\:{is}\:{not}\:{a}\:{number}.\:{but}\:\:{both}\:{numerator} \\ $$$${and}\:{denominator}\:{are}\:{numbers}. \\ $$
Commented by 121194 last updated on 12/Mar/19
one may think that (1/0)=∞, but that not entire true think of lim_(x→0) (1/x) lets aproach it 2 ways 1→1 0.5→2 0.1→10 0.01→100 0.001→1000 as you can see as close we aproach x 1/x grow without any limit, so lim_(x→0^+ ) (1/x)=+∞ but that only 1 path, takes the 2nd one −1→−1 −0.5→−2 −0.1→−10 −0.01→−100 as you see it grow in complet opost direction, as lim_(x→0^− ) (1/x)=−∞ since the 2 limits are diferents we can′t say that the limit exist so lim_(x→0) (1/x)=∄ btw there any analogous of ∞ to complex, the complex infinite ∞^∼ it basicaly a “number” with high modulos but unknow argument
$$\mathrm{one}\:\mathrm{may}\:\mathrm{think}\:\mathrm{that}\:\frac{\mathrm{1}}{\mathrm{0}}=\infty,\:\mathrm{but}\:\mathrm{that}\:\mathrm{not}\:\mathrm{entire}\:\mathrm{true} \\ $$$$\mathrm{think}\:\mathrm{of} \\ $$$$\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\frac{\mathrm{1}}{{x}} \\ $$$$\mathrm{lets}\:\mathrm{aproach}\:\mathrm{it}\:\mathrm{2}\:\mathrm{ways} \\ $$$$\mathrm{1}\rightarrow\mathrm{1} \\ $$$$\mathrm{0}.\mathrm{5}\rightarrow\mathrm{2} \\ $$$$\mathrm{0}.\mathrm{1}\rightarrow\mathrm{10} \\ $$$$\mathrm{0}.\mathrm{01}\rightarrow\mathrm{100} \\ $$$$\mathrm{0}.\mathrm{001}\rightarrow\mathrm{1000} \\ $$$${as}\:{you}\:{can}\:{see}\:{as}\:{close}\:{we}\:{aproach}\:{x}\:\mathrm{1}/{x}\:{grow} \\ $$$${without}\:{any}\:{limit},\:{so} \\ $$$$\underset{{x}\rightarrow\mathrm{0}^{+} } {\mathrm{lim}}\frac{\mathrm{1}}{{x}}=+\infty\: \\ $$$${but}\:{that}\:{only}\:\mathrm{1}\:{path},\:{takes}\:{the}\:\mathrm{2}{nd}\:{one} \\ $$$$−\mathrm{1}\rightarrow−\mathrm{1} \\ $$$$−\mathrm{0}.\mathrm{5}\rightarrow−\mathrm{2} \\ $$$$−\mathrm{0}.\mathrm{1}\rightarrow−\mathrm{10} \\ $$$$−\mathrm{0}.\mathrm{01}\rightarrow−\mathrm{100} \\ $$$${as}\:{you}\:{see}\:{it}\:{grow}\:{in}\:{complet}\:{opost}\:{direction},\:{as} \\ $$$$\underset{{x}\rightarrow\mathrm{0}^{−} } {\mathrm{lim}}\frac{\mathrm{1}}{{x}}=−\infty \\ $$$${since}\:{the}\:\mathrm{2}\:{limits}\:{are}\:{diferents}\:{we}\:{can}'{t}\:{say}\:{that} \\ $$$${the}\:{limit}\:{exist}\:{so} \\ $$$$\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\frac{\mathrm{1}}{{x}}=\nexists \\ $$$${btw}\:{there}\:{any}\:{analogous}\:{of}\:\infty\:{to}\:{complex},\:{the} \\ $$$${complex}\:{infinite}\:\overset{\sim} {\infty} \\ $$$${it}\:{basicaly}\:{a}\:“{number}''\:{with}\:{high}\:{modulos}\:{but} \\ $$$${unknow}\:{argument} \\ $$
Commented by Joel578 last updated on 12/Mar/19
(1/0) is actually undefined Now, let f(x) = (1/x) If we take x = 0.00000001, f(x) = 100000000 Next, if x getting smaller, very close to zero then our f(x) is getting larger Next, x now is very very very smaller, then our f(x) is very very very large. In this context, we can denote this as lim_(x→0^+ ) (1/x) = (1/0) = ∞ As x is getting smaller, very close to zero then its value will reach an arbitrarily large number. How large? Very large. And we denote this with “∞” So, in my opinion “∞” is a concept to describe an arbitrarily large number, but it isn′t a number
$$\frac{\mathrm{1}}{\mathrm{0}}\:\mathrm{is}\:\mathrm{actually}\:\mathrm{undefined} \\ $$$$\mathrm{Now},\:\mathrm{let}\:{f}\left({x}\right)\:=\:\frac{\mathrm{1}}{{x}} \\ $$$$\mathrm{If}\:\mathrm{we}\:\mathrm{take}\:{x}\:=\:\mathrm{0}.\mathrm{00000001},\:{f}\left({x}\right)\:=\:\mathrm{100000000} \\ $$$$\mathrm{Next},\:\mathrm{if}\:{x}\:\mathrm{getting}\:\mathrm{smaller},\:\mathrm{very}\:\mathrm{close}\:\mathrm{to}\:\mathrm{zero} \\ $$$$\mathrm{then}\:\mathrm{our}\:{f}\left({x}\right)\:\mathrm{is}\:\mathrm{getting}\:\mathrm{larger} \\ $$$$\mathrm{Next},\:{x}\:\mathrm{now}\:\mathrm{is}\:\mathrm{very}\:\mathrm{very}\:\mathrm{very}\:\mathrm{smaller},\:\mathrm{then} \\ $$$$\mathrm{our}\:{f}\left({x}\right)\:\mathrm{is}\:\mathrm{very}\:\mathrm{very}\:\mathrm{very}\:\mathrm{large}. \\ $$$$\mathrm{In}\:\mathrm{this}\:\mathrm{context},\:\mathrm{we}\:\mathrm{can}\:\mathrm{denote}\:\mathrm{this}\:\mathrm{as} \\ $$$$\underset{{x}\rightarrow\mathrm{0}^{+} } {\mathrm{lim}}\:\frac{\mathrm{1}}{{x}}\:=\:\frac{\mathrm{1}}{\mathrm{0}}\:=\:\infty \\ $$$$\mathrm{As}\:{x}\:\mathrm{is}\:\mathrm{getting}\:\mathrm{smaller},\:\mathrm{very}\:\mathrm{close}\:\mathrm{to}\:\mathrm{zero} \\ $$$$\mathrm{then}\:\mathrm{its}\:\mathrm{value}\:\mathrm{will}\:\mathrm{reach}\:\mathrm{an}\:\mathrm{arbitrarily}\:\mathrm{large}\:\mathrm{number}. \\ $$$$\mathrm{How}\:\mathrm{large}?\:\mathrm{Very}\:\mathrm{large}.\:\mathrm{And}\:\mathrm{we}\:\mathrm{denote}\:\mathrm{this}\:\mathrm{with}\:“\infty'' \\ $$$$\mathrm{So},\:\mathrm{in}\:\mathrm{my}\:\mathrm{opinion}\:“\infty''\:\mathrm{is}\:\mathrm{a}\:\mathrm{concept}\:\mathrm{to}\:\mathrm{describe} \\ $$$$\mathrm{an}\:\mathrm{arbitrarily}\:\mathrm{large}\:\mathrm{number},\:\mathrm{but}\:\mathrm{it}\:\mathrm{isn}'\mathrm{t}\:\mathrm{a}\:\mathrm{number} \\ $$
Commented by Joel578 last updated on 12/Mar/19
That′ s what I know. I am open for any critics if I made any mistakes
$$\mathrm{That}'\:\mathrm{s}\:\mathrm{what}\:\mathrm{I}\:\mathrm{know}.\:\mathrm{I}\:\mathrm{am}\:\mathrm{open}\:\mathrm{for}\:\mathrm{any}\:\mathrm{critics}\:\mathrm{if} \\ $$$$\mathrm{I}\:\mathrm{made}\:\mathrm{any}\:\mathrm{mistakes} \\ $$
Commented by Kunal12588 last updated on 12/Mar/19
thank you very much sirs.
$${thank}\:{you}\:{very}\:{much}\:{sirs}. \\ $$
Commented by prakash jain last updated on 12/Mar/19
please visit the below link for definition of complex infinity http://mathworld.wolfram.com/ComplexInfinity.html

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *