Menu Close

Evaluate-the-sum-2-3-1-2-2-3-2-1-2-3-3-4-1-2-n-1-3-2-n-1-

Tinku Tara 0 Comments
Pin




Question Number 121949 by liberty last updated on 12/Nov/20
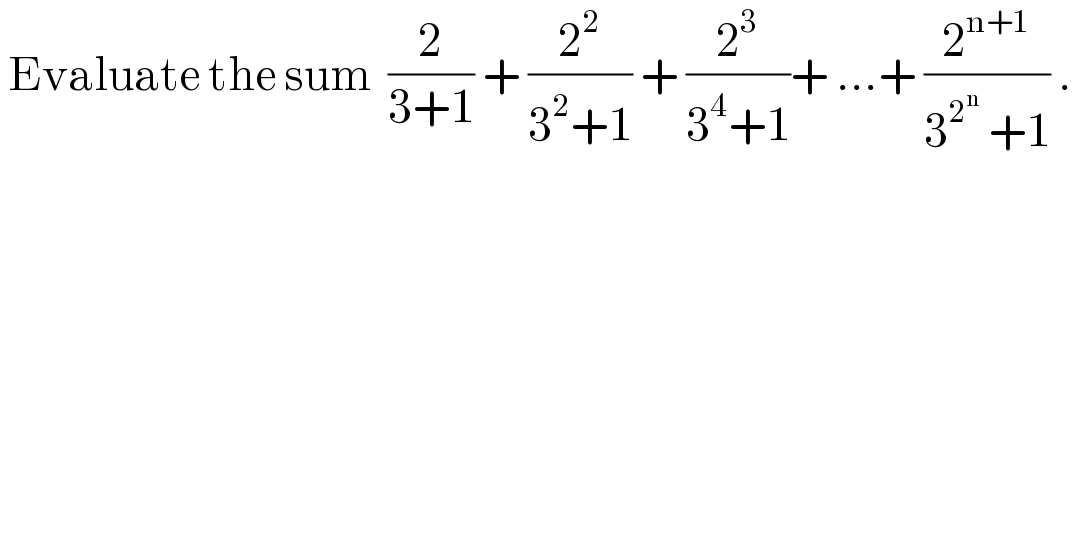
Evaluate the sum (2/(3+1)) + (2^2 /(3^2 +1)) + (2^3 /(3^4 +1))+ ...+ (2^(n+1) /(3^2^n +1)) .
$$\:\mathrm{Evaluate}\:\mathrm{the}\:\mathrm{sum}\:\:\frac{\mathrm{2}}{\mathrm{3}+\mathrm{1}}\:+\:\frac{\mathrm{2}^{\mathrm{2}} }{\mathrm{3}^{\mathrm{2}} +\mathrm{1}}\:+\:\frac{\mathrm{2}^{\mathrm{3}} }{\mathrm{3}^{\mathrm{4}} +\mathrm{1}}+\:…+\:\frac{\mathrm{2}^{\mathrm{n}+\mathrm{1}} }{\mathrm{3}^{\mathrm{2}^{\mathrm{n}} } \:+\mathrm{1}}\:. \\ $$
Answered by bobhans last updated on 12/Nov/20
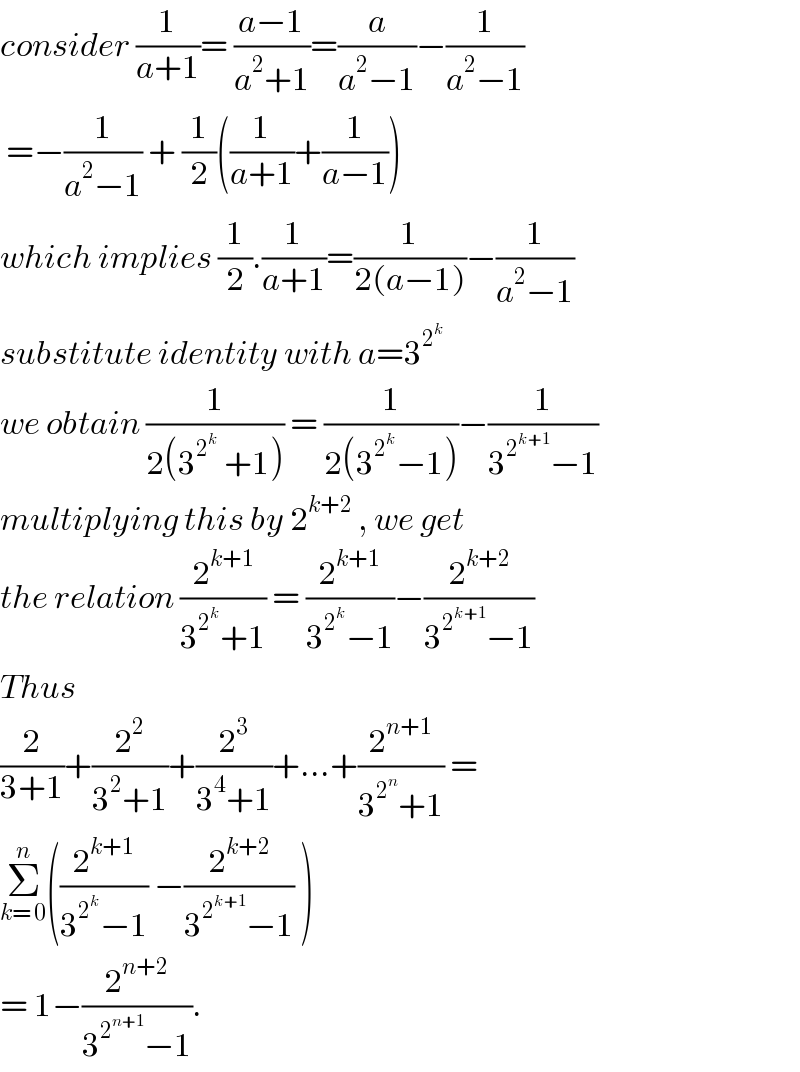
consider (1/(a+1))= ((a−1)/(a^2 +1))=(a/(a^2 −1))−(1/(a^2 −1)) =−(1/(a^2 −1)) + (1/2)((1/(a+1))+(1/(a−1))) which implies (1/2).(1/(a+1))=(1/(2(a−1)))−(1/(a^2 −1)) substitute identity with a=3^2^k we obtain (1/(2(3^2^k +1))) = (1/(2(3^2^k −1)))−(1/(3^2^(k+1) −1)) multiplying this by 2^(k+2) , we get the relation (2^(k+1) /(3^2^k +1)) = (2^(k+1) /(3^2^k −1))−(2^(k+2) /(3^2^(k+1) −1)) Thus (2/(3+1))+(2^2 /(3^2 +1))+(2^3 /(3^4 +1))+...+(2^(n+1) /(3^2^n +1)) = Σ_(k= 0) ^n ((2^(k+1) /(3^2^k −1)) −(2^(k+2) /(3^2^(k+1) −1)) ) = 1−(2^(n+2) /(3^2^(n+1) −1)).
$${consider}\:\frac{\mathrm{1}}{{a}+\mathrm{1}}=\:\frac{{a}−\mathrm{1}}{{a}^{\mathrm{2}} +\mathrm{1}}=\frac{{a}}{{a}^{\mathrm{2}} −\mathrm{1}}−\frac{\mathrm{1}}{{a}^{\mathrm{2}} −\mathrm{1}} \\ $$$$\:=−\frac{\mathrm{1}}{{a}^{\mathrm{2}} −\mathrm{1}}\:+\:\frac{\mathrm{1}}{\mathrm{2}}\left(\frac{\mathrm{1}}{{a}+\mathrm{1}}+\frac{\mathrm{1}}{{a}−\mathrm{1}}\right) \\ $$$${which}\:{implies}\:\frac{\mathrm{1}}{\mathrm{2}}.\frac{\mathrm{1}}{{a}+\mathrm{1}}=\frac{\mathrm{1}}{\mathrm{2}\left({a}−\mathrm{1}\right)}−\frac{\mathrm{1}}{{a}^{\mathrm{2}} −\mathrm{1}} \\ $$$${substitute}\:{identity}\:{with}\:{a}=\mathrm{3}^{\mathrm{2}^{{k}} } \\ $$$${we}\:{obtain}\:\frac{\mathrm{1}}{\mathrm{2}\left(\mathrm{3}^{\mathrm{2}^{{k}} } \:+\mathrm{1}\right)}\:=\:\frac{\mathrm{1}}{\mathrm{2}\left(\mathrm{3}^{\mathrm{2}^{{k}} } −\mathrm{1}\right)}−\frac{\mathrm{1}}{\mathrm{3}^{\mathrm{2}^{{k}+\mathrm{1}} } −\mathrm{1}} \\ $$$${multiplying}\:{this}\:{by}\:\mathrm{2}^{{k}+\mathrm{2}} \:,\:{we}\:{get}\: \\ $$$${the}\:{relation}\:\frac{\mathrm{2}^{{k}+\mathrm{1}} }{\mathrm{3}^{\mathrm{2}^{{k}} } +\mathrm{1}}\:=\:\frac{\mathrm{2}^{{k}+\mathrm{1}} }{\mathrm{3}^{\mathrm{2}^{{k}} } −\mathrm{1}}−\frac{\mathrm{2}^{{k}+\mathrm{2}} }{\mathrm{3}^{\mathrm{2}^{{k}+\mathrm{1}} } −\mathrm{1}} \\ $$$${Thus}\: \\ $$$$\frac{\mathrm{2}}{\mathrm{3}+\mathrm{1}}+\frac{\mathrm{2}^{\mathrm{2}} }{\mathrm{3}^{\mathrm{2}} +\mathrm{1}}+\frac{\mathrm{2}^{\mathrm{3}} }{\mathrm{3}^{\mathrm{4}} +\mathrm{1}}+…+\frac{\mathrm{2}^{{n}+\mathrm{1}} }{\mathrm{3}^{\mathrm{2}^{{n}} } +\mathrm{1}}\:= \\ $$$$\underset{{k}=\:\mathrm{0}} {\overset{{n}} {\sum}}\left(\frac{\mathrm{2}^{{k}+\mathrm{1}} }{\mathrm{3}^{\mathrm{2}^{{k}} } −\mathrm{1}}\:−\frac{\mathrm{2}^{{k}+\mathrm{2}} }{\mathrm{3}^{\mathrm{2}^{{k}+\mathrm{1}} } −\mathrm{1}}\:\right) \\ $$$$=\:\mathrm{1}−\frac{\mathrm{2}^{{n}+\mathrm{2}} }{\mathrm{3}^{\mathrm{2}^{{n}+\mathrm{1}} } −\mathrm{1}}.\: \\ $$
Commented by liberty last updated on 12/Nov/20
good....
$$\mathrm{good}…. \\ $$
Commented by sewak last updated on 17/Nov/20
Quite good
$$\mathrm{Quite}\:\mathrm{good} \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *