Question Number 121962 by bemath last updated on 13/Nov/20
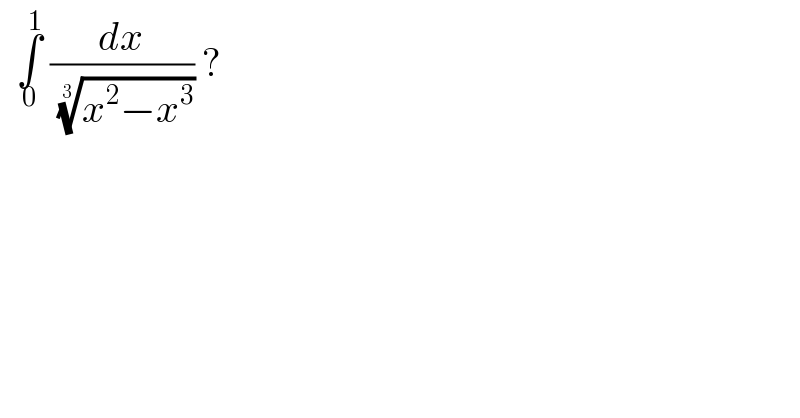
$$\:\:\underset{\mathrm{0}} {\overset{\mathrm{1}} {\int}}\:\frac{{dx}}{\:\sqrt[{\mathrm{3}\:}]{{x}^{\mathrm{2}} −{x}^{\mathrm{3}} }}\:?\: \\ $$
Answered by MJS_new last updated on 13/Nov/20
![∫_0 ^1 (dx/((x^2 −x^3 )^(1/3) ))=∫_0 ^1 (dx/(x^(2/3) (1−x)^(1/3) ))= [t=(x^(1/3) /((1−x)^(1/3) )) → dx=3x^(2/3) (1−x)^(4/3) dt] =3∫_0 ^∞ (dt/(t^3 +1))=∫_0 ^∞ (dt/(t+1))−(1/2)∫_0 ^∞ ((2t−1)/(t^2 −t+1))+(3/2)∫_0 ^∞ (dt/(t^2 −t+1))= =[ln ∣t+1∣ −(1/2)ln (t^2 −t+1) +(√3)arctan ((2t−1)/( (√3)))]_0 ^∞ = =((2π(√3))/3)](https://www.tinkutara.com/question/Q121968.png)
$$\underset{\mathrm{0}} {\overset{\mathrm{1}} {\int}}\frac{{dx}}{\left({x}^{\mathrm{2}} −{x}^{\mathrm{3}} \right)^{\mathrm{1}/\mathrm{3}} }=\underset{\mathrm{0}} {\overset{\mathrm{1}} {\int}}\frac{{dx}}{{x}^{\mathrm{2}/\mathrm{3}} \left(\mathrm{1}−{x}\right)^{\mathrm{1}/\mathrm{3}} }= \\ $$$$\:\:\:\:\:\left[{t}=\frac{{x}^{\mathrm{1}/\mathrm{3}} }{\left(\mathrm{1}−{x}\right)^{\mathrm{1}/\mathrm{3}} }\:\rightarrow\:{dx}=\mathrm{3}{x}^{\mathrm{2}/\mathrm{3}} \left(\mathrm{1}−{x}\right)^{\mathrm{4}/\mathrm{3}} {dt}\right] \\ $$$$=\mathrm{3}\underset{\mathrm{0}} {\overset{\infty} {\int}}\frac{{dt}}{{t}^{\mathrm{3}} +\mathrm{1}}=\underset{\mathrm{0}} {\overset{\infty} {\int}}\frac{{dt}}{{t}+\mathrm{1}}−\frac{\mathrm{1}}{\mathrm{2}}\underset{\mathrm{0}} {\overset{\infty} {\int}}\frac{\mathrm{2}{t}−\mathrm{1}}{{t}^{\mathrm{2}} −{t}+\mathrm{1}}+\frac{\mathrm{3}}{\mathrm{2}}\underset{\mathrm{0}} {\overset{\infty} {\int}}\frac{{dt}}{{t}^{\mathrm{2}} −{t}+\mathrm{1}}= \\ $$$$=\left[\mathrm{ln}\:\mid{t}+\mathrm{1}\mid\:−\frac{\mathrm{1}}{\mathrm{2}}\mathrm{ln}\:\left({t}^{\mathrm{2}} −{t}+\mathrm{1}\right)\:+\sqrt{\mathrm{3}}\mathrm{arctan}\:\frac{\mathrm{2}{t}−\mathrm{1}}{\:\sqrt{\mathrm{3}}}\right]_{\mathrm{0}} ^{\infty} = \\ $$$$=\frac{\mathrm{2}\pi\sqrt{\mathrm{3}}}{\mathrm{3}} \\ $$
Commented by bemath last updated on 13/Nov/20
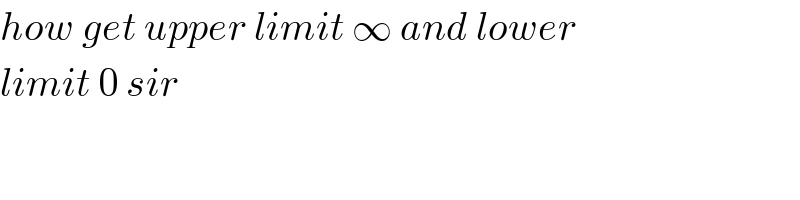
$${how}\:{get}\:{upper}\:{limit}\:\infty\:{and}\:{lower} \\ $$$${limit}\:\mathrm{0}\:{sir} \\ $$
Commented by MJS_new last updated on 13/Nov/20

$${t}=\frac{{x}^{\mathrm{1}/\mathrm{3}} }{\left(\mathrm{1}−{x}\right)^{\mathrm{1}/\mathrm{3}} } \\ $$$${x}=\mathrm{0}\:\Rightarrow\:{t}=\mathrm{0} \\ $$$${x}\rightarrow\mathrm{1}^{−} \:\Rightarrow\:{t}\rightarrow\infty \\ $$
Commented by MJS_new last updated on 13/Nov/20
$$\mathrm{corrected}\:\mathrm{a}\:\mathrm{typo}… \\ $$
Commented by bemath last updated on 13/Nov/20
$${oo}\:{yes}\:{thank}\:{you}\:{sir} \\ $$
Answered by Dwaipayan Shikari last updated on 13/Nov/20
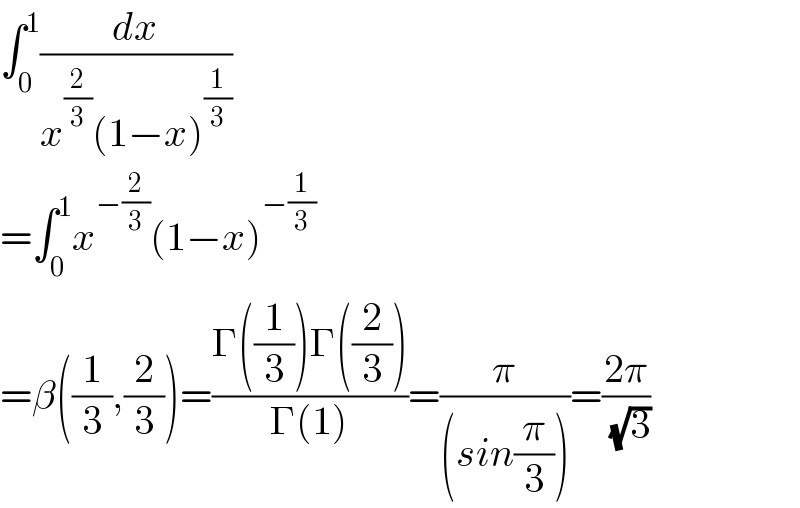
$$\int_{\mathrm{0}} ^{\mathrm{1}} \frac{{dx}}{{x}^{\frac{\mathrm{2}}{\mathrm{3}}} \left(\mathrm{1}−{x}\right)^{\frac{\mathrm{1}}{\mathrm{3}}} } \\ $$$$=\int_{\mathrm{0}} ^{\mathrm{1}} {x}^{−\frac{\mathrm{2}}{\mathrm{3}}} \left(\mathrm{1}−{x}\right)^{−\frac{\mathrm{1}}{\mathrm{3}}} \\ $$$$=\beta\left(\frac{\mathrm{1}}{\mathrm{3}},\frac{\mathrm{2}}{\mathrm{3}}\right)=\frac{\Gamma\left(\frac{\mathrm{1}}{\mathrm{3}}\right)\Gamma\left(\frac{\mathrm{2}}{\mathrm{3}}\right)}{\Gamma\left(\mathrm{1}\right)}=\frac{\pi}{\left({sin}\frac{\pi}{\mathrm{3}}\right)}=\frac{\mathrm{2}\pi}{\:\sqrt{\mathrm{3}}} \\ $$
