Question Number 56510 by Tawa1 last updated on 17/Mar/19

Commented by MJS last updated on 17/Mar/19
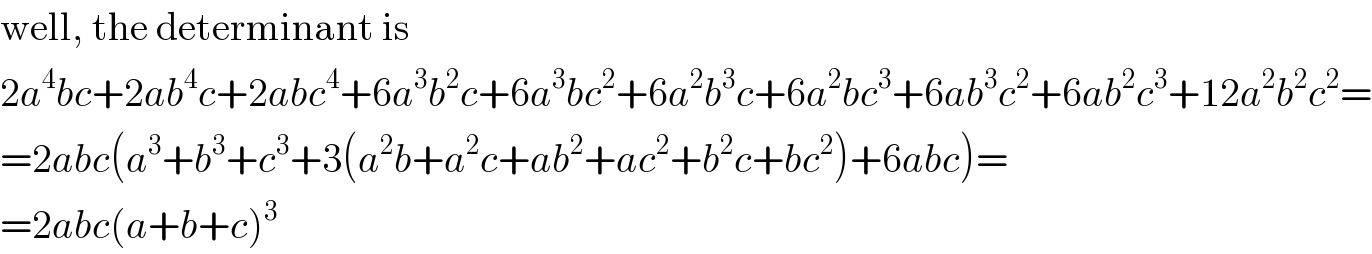
$$\mathrm{well},\:\mathrm{the}\:\mathrm{determinant}\:\mathrm{is} \\ $$$$\mathrm{2}{a}^{\mathrm{4}} {bc}+\mathrm{2}{ab}^{\mathrm{4}} {c}+\mathrm{2}{abc}^{\mathrm{4}} +\mathrm{6}{a}^{\mathrm{3}} {b}^{\mathrm{2}} {c}+\mathrm{6}{a}^{\mathrm{3}} {bc}^{\mathrm{2}} +\mathrm{6}{a}^{\mathrm{2}} {b}^{\mathrm{3}} {c}+\mathrm{6}{a}^{\mathrm{2}} {bc}^{\mathrm{3}} +\mathrm{6}{ab}^{\mathrm{3}} {c}^{\mathrm{2}} +\mathrm{6}{ab}^{\mathrm{2}} {c}^{\mathrm{3}} +\mathrm{12}{a}^{\mathrm{2}} {b}^{\mathrm{2}} {c}^{\mathrm{2}} = \\ $$$$=\mathrm{2}{abc}\left({a}^{\mathrm{3}} +{b}^{\mathrm{3}} +{c}^{\mathrm{3}} +\mathrm{3}\left({a}^{\mathrm{2}} {b}+{a}^{\mathrm{2}} {c}+{ab}^{\mathrm{2}} +{ac}^{\mathrm{2}} +{b}^{\mathrm{2}} {c}+{bc}^{\mathrm{2}} \right)+\mathrm{6}{abc}\right)= \\ $$$$=\mathrm{2}{abc}\left({a}+{b}+{c}\right)^{\mathrm{3}} \\ $$
Commented by Tawa1 last updated on 18/Mar/19
$$\mathrm{God}\:\mathrm{bless}\:\mathrm{you}\:\mathrm{sir} \\ $$
Answered by tanmay.chaudhury50@gmail.com last updated on 18/Mar/19
![trying to solve by another method ... determinant △ has degree=6 1)if you put a=0 in △ ∣(b+c)^2 0 0∣ ∣ b^2 c^2 b^2 ∣ ←its value is 0 ∣ c^2 c^2 b^2 ∣ so a is a factor of △ .similarly b is also a factor of △ and c also a factor. so abc is fsctor of △ now put condition a+b+c=0 ∣(−a)^2 a^2 a^2 ∣ ∣b^2 (−b)^2 b^2 ∣ ∣c^2 c^2 (−c)^2 ∣ the value of this determinant=0 here look three coloumn are identical so (a+b+c)^(3−1) →(a+b+c)^2 is factor of now degree of (abc)(a+b+c)^2 is 5 but the degree of △=6 so △=Kabc(a+b+c)^2 ×(a+b+c) [red coloured (a+b+c) is symmetric function of degree=1 a^2 +b^2 +c^2 snd ab+bc+ca symmetric gunction of degrer=2 etc] so △=kabc(a+b+c)^2 (a+b+c) △=∣(b+c)^2 a^2 a^2 ∣ ∣b^2 (a+c)^2 b^2 ∣ ∣c^2 c^2 (a+b)^2 ∣ =kabc(a+b+c)^3 now put a=b=c=1 both side.. ∣ 4 1 1∣ ∣ 1 4 1∣ =k×1×1×1×27 ∣ 1 1 4∣ 54=27k so k=2 hence answer is 2abc(a+b+c)^3](https://www.tinkutara.com/question/Q56550.png)
$${trying}\:{to}\:{solve}\:{by}\:{another}\:{method}\:… \\ $$$${determinant}\:\bigtriangleup\:{has}\:{degree}=\mathrm{6} \\ $$$$\left.\mathrm{1}\right){if}\:{you}\:{put}\:{a}=\mathrm{0}\:{in}\:\bigtriangleup \\ $$$$\mid\left({b}+{c}\right)^{\mathrm{2}} \:\:\:\:\:\:\:\mathrm{0}\:\:\:\:\:\:\:\:\mathrm{0}\mid \\ $$$$\mid\:\:\:{b}^{\mathrm{2}} \:\:\:\:\:\:\:\:\:\:\:\:\:\:{c}^{\mathrm{2}} \:\:\:\:\:\:\:{b}^{\mathrm{2}} \mid\:\leftarrow{its}\:{value}\:{is}\:\mathrm{0} \\ $$$$\mid\:{c}^{\mathrm{2}} \:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:{c}^{\mathrm{2}} \:\:\:\:\:\:\:{b}^{\mathrm{2}} \mid \\ $$$$\:{so}\:{a}\:{is}\:{a}\:{factor}\:{of}\:\bigtriangleup\:.\boldsymbol{{similarly}}\:\boldsymbol{{b}}\:\boldsymbol{{is}}\:\boldsymbol{{also}}\: \\ $$$$\boldsymbol{{a}}\:\boldsymbol{{factor}}\:\boldsymbol{{of}}\:\bigtriangleup\:{and}\:{c}\:{also}\:{a}\:{factor}. \\ $$$${so}\:{abc}\:{is}\:{fsctor}\:{of}\:\bigtriangleup \\ $$$${now}\:{put}\:{condition}\:{a}+{b}+{c}=\mathrm{0} \\ $$$$\mid\left(−{a}\right)^{\mathrm{2}} \:\:\:{a}^{\mathrm{2}} \:\:\:\:\:\:\:\:\:\:\:\:\:{a}^{\mathrm{2}} \:\:\mid \\ $$$$\mid{b}^{\mathrm{2}} \:\:\:\:\:\:\:\:\:\left(−{b}\right)^{\mathrm{2}} \:\:\:\:\:\:\:\:\:{b}^{\mathrm{2}} \:\:\:\mid \\ $$$$\mid{c}^{\mathrm{2}} \:\:\:\:\:\:\:\:\:\:\:\:{c}^{\mathrm{2}} \:\:\:\:\:\:\:\:\left(−{c}\right)^{\mathrm{2}} \mid \\ $$$${the}\:{value}\:{of}\:{this}\:{determinant}=\mathrm{0} \\ $$$${here}\:{look}\:{three}\:{coloumn}\:{are}\:{identical} \\ $$$${so}\:\left({a}+{b}+{c}\right)^{\mathrm{3}−\mathrm{1}} \rightarrow\left({a}+{b}+{c}\right)^{\mathrm{2}} \:{is}\:{factor}\:{of}\:\: \\ $$$${now}\:{degree}\:{of}\:\left({abc}\right)\left({a}+{b}+{c}\right)^{\mathrm{2}} \:{is}\:\mathrm{5}\: \\ $$$${but}\:{the}\:{degree}\:{of}\:\bigtriangleup=\mathrm{6} \\ $$$${so}\:\bigtriangleup={Kabc}\left({a}+{b}+{c}\right)^{\mathrm{2}} ×\left({a}+{b}+{c}\right) \\ $$$$\left[{red}\:{coloured}\:\left({a}+{b}+{c}\right)\:{is}\:{symmetric}\:{function}\right. \\ $$$${of}\:{degree}=\mathrm{1} \\ $$$${a}^{\mathrm{2}} +{b}^{\mathrm{2}} +{c}^{\mathrm{2}} \:{snd}\:{ab}+{bc}+{ca}\:{symmetric}\:{gunction} \\ $$$$\left.{of}\:{degrer}=\mathrm{2}\:\:{etc}\right] \\ $$$${so}\:\bigtriangleup={kabc}\left({a}+{b}+{c}\right)^{\mathrm{2}} \left({a}+{b}+{c}\right) \\ $$$$\bigtriangleup=\mid\left({b}+{c}\right)^{\mathrm{2}} \:\:\:\:{a}^{\mathrm{2}} \:\:\:\:\:\:\:\:\:\:\:\:{a}^{\mathrm{2}} \:\:\mid \\ $$$$\:\:\:\:\:\:\:\:\:\mid{b}^{\mathrm{2}} \:\:\:\:\:\:\:\left({a}+{c}\right)^{\mathrm{2}} \:\:\:\:\:\:\:\:\:\:\:\:{b}^{\mathrm{2}} \mid \\ $$$$\:\:\:\:\:\:\:\:\mid{c}^{\mathrm{2}} \:\:\:\:\:\:\:\:\:{c}^{\mathrm{2}} \:\:\:\:\:\:\:\:\:\:\:\:\left({a}+{b}\right)^{\mathrm{2}} \mid \\ $$$$={kabc}\left({a}+{b}+{c}\right)^{\mathrm{3}} \\ $$$${now}\:{put}\:{a}={b}={c}=\mathrm{1}\:{both}\:{side}.. \\ $$$$\mid\:\:\mathrm{4}\:\:\:\:\:\:\:\mathrm{1}\:\:\:\:\:\:\:\mathrm{1}\mid \\ $$$$\mid\:\:\mathrm{1}\:\:\:\:\:\:\:\mathrm{4}\:\:\:\:\:\:\:\mathrm{1}\mid\:\:={k}×\mathrm{1}×\mathrm{1}×\mathrm{1}×\mathrm{27} \\ $$$$\mid\:\mathrm{1}\:\:\:\:\:\:\:\:\mathrm{1}\:\:\:\:\:\:\:\:\mathrm{4}\mid \\ $$$$\mathrm{54}=\mathrm{27}{k}\:\:\:{so}\:{k}=\mathrm{2} \\ $$$${hence}\:{answer}\:{is}\:\mathrm{2}{abc}\left({a}+{b}+{c}\right)^{\mathrm{3}} \\ $$$$ \\ $$
Commented by Tawa1 last updated on 18/Mar/19
$$\mathrm{God}\:\mathrm{bless}\:\mathrm{you}\:\mathrm{sir} \\ $$
