Question Number 71089 by 20190927 last updated on 11/Oct/19
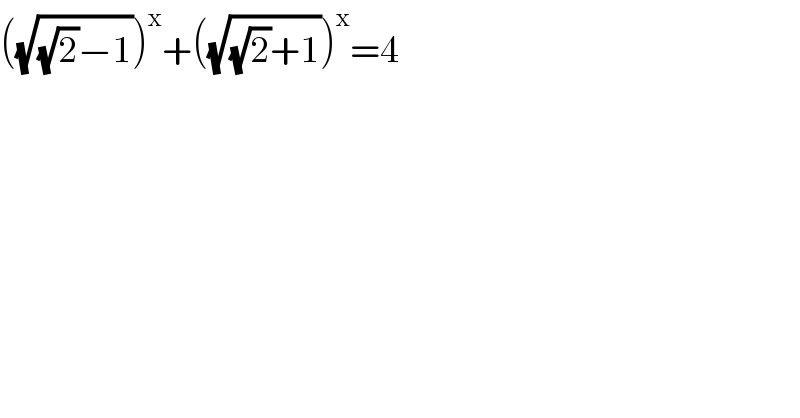
$$\left(\sqrt{\sqrt{\mathrm{2}}−\mathrm{1}}\right)^{\mathrm{x}} +\left(\sqrt{\sqrt{\mathrm{2}}+\mathrm{1}}\right)^{\mathrm{x}} =\mathrm{4} \\ $$
Answered by Henri Boucatchou last updated on 11/Oct/19
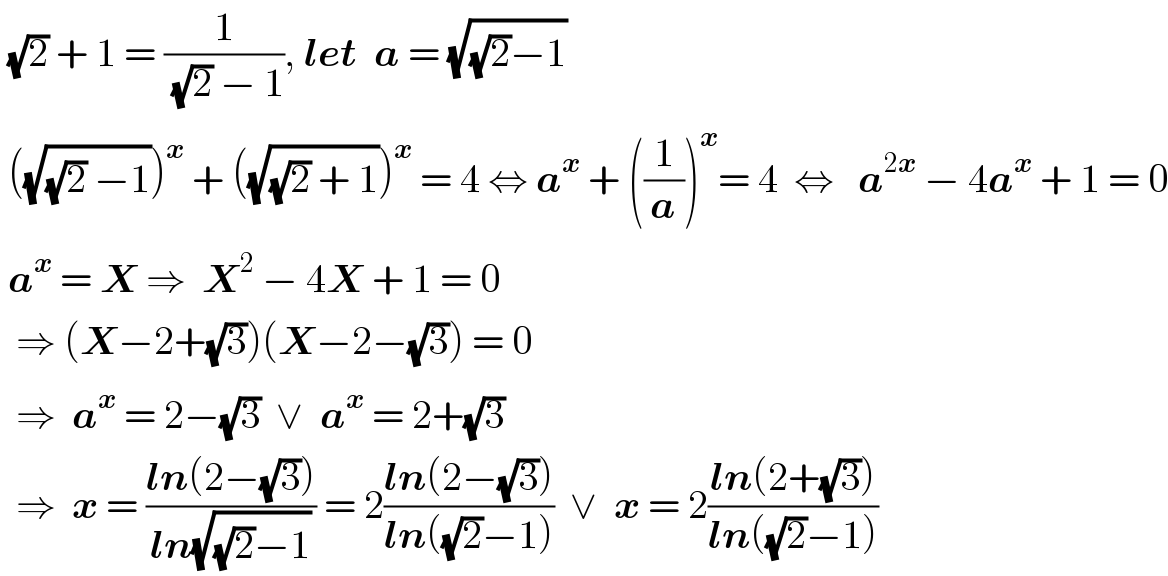
$$\:\sqrt{\mathrm{2}}\:+\:\mathrm{1}\:=\:\frac{\mathrm{1}}{\:\sqrt{\mathrm{2}}\:−\:\mathrm{1}},\:\boldsymbol{{let}}\:\:\boldsymbol{{a}}\:=\:\sqrt{\sqrt{\mathrm{2}}−\mathrm{1}} \\ $$$$\:\left(\sqrt{\sqrt{\mathrm{2}}\:−\mathrm{1}}\right)^{\boldsymbol{{x}}} \:+\:\left(\sqrt{\sqrt{\mathrm{2}}\:+\:\mathrm{1}}\right)^{\boldsymbol{{x}}} \:=\:\mathrm{4}\:\Leftrightarrow\:\boldsymbol{{a}}^{\boldsymbol{{x}}} \:+\:\left(\frac{\mathrm{1}}{\boldsymbol{{a}}}\right)^{\boldsymbol{{x}}} =\:\mathrm{4}\:\:\Leftrightarrow\:\:\:\boldsymbol{{a}}^{\mathrm{2}\boldsymbol{{x}}} \:−\:\mathrm{4}\boldsymbol{{a}}^{\boldsymbol{{x}}} \:+\:\mathrm{1}\:=\:\mathrm{0} \\ $$$$\:\boldsymbol{{a}}^{\boldsymbol{{x}}} \:=\:\boldsymbol{{X}}\:\Rightarrow\:\:\boldsymbol{{X}}^{\mathrm{2}} \:−\:\mathrm{4}\boldsymbol{{X}}\:+\:\mathrm{1}\:=\:\mathrm{0} \\ $$$$\:\:\Rightarrow\:\left(\boldsymbol{{X}}−\mathrm{2}+\sqrt{\mathrm{3}}\right)\left(\boldsymbol{{X}}−\mathrm{2}−\sqrt{\mathrm{3}}\right)\:=\:\mathrm{0} \\ $$$$\:\:\Rightarrow\:\:\boldsymbol{{a}}^{\boldsymbol{{x}}} \:=\:\mathrm{2}−\sqrt{\mathrm{3}}\:\:\vee\:\:\boldsymbol{{a}}^{\boldsymbol{{x}}} \:=\:\mathrm{2}+\sqrt{\mathrm{3}} \\ $$$$\:\:\Rightarrow\:\:\boldsymbol{{x}}\:=\:\frac{\boldsymbol{{ln}}\left(\mathrm{2}−\sqrt{\mathrm{3}}\right)}{\boldsymbol{{ln}}\sqrt{\sqrt{\mathrm{2}}−\mathrm{1}}}\:=\:\mathrm{2}\frac{\boldsymbol{{ln}}\left(\mathrm{2}−\sqrt{\mathrm{3}}\right)}{\boldsymbol{{ln}}\left(\sqrt{\mathrm{2}}−\mathrm{1}\right)}\:\:\vee\:\:\boldsymbol{{x}}\:=\:\mathrm{2}\frac{\boldsymbol{{ln}}\left(\mathrm{2}+\sqrt{\mathrm{3}}\right)}{\boldsymbol{{ln}}\left(\sqrt{\mathrm{2}}−\mathrm{1}\right)} \\ $$
