Question Number 56688 by pieroo last updated on 21/Mar/19

$$\mathrm{How}\:\mathrm{many}\:\mathrm{odd}\:\mathrm{numbers},\:\mathrm{greater}\:\mathrm{than} \\ $$$$\mathrm{60000},\:\mathrm{can}\:\mathrm{be}\:\mathrm{made}\:\mathrm{from}\:\mathrm{the}\:\mathrm{digits} \\ $$$$\mathrm{5},\mathrm{6},\mathrm{7},\mathrm{8},\mathrm{9},\mathrm{0},\:\mathrm{if}\:\mathrm{no}\:\mathrm{number}\:\mathrm{contains}\:\mathrm{any} \\ $$$$\mathrm{digit}\:\mathrm{more}\:\mathrm{than}\:\mathrm{ones}? \\ $$
Answered by mr W last updated on 22/Mar/19
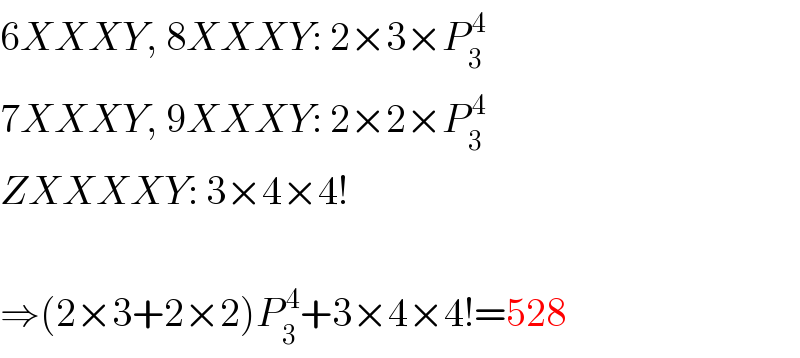
$$\mathrm{6}{XXXY},\:\mathrm{8}{XXXY}:\:\mathrm{2}×\mathrm{3}×{P}_{\mathrm{3}} ^{\:\mathrm{4}} \\ $$$$\mathrm{7}{XXXY},\:\mathrm{9}{XXXY}:\:\mathrm{2}×\mathrm{2}×{P}_{\mathrm{3}} ^{\:\mathrm{4}} \\ $$$${ZXXXXY}:\:\mathrm{3}×\mathrm{4}×\mathrm{4}! \\ $$$$ \\ $$$$\Rightarrow\left(\mathrm{2}×\mathrm{3}+\mathrm{2}×\mathrm{2}\right){P}_{\mathrm{3}} ^{\:\mathrm{4}} +\mathrm{3}×\mathrm{4}×\mathrm{4}!=\mathrm{528} \\ $$
Commented by malwaan last updated on 22/Mar/19
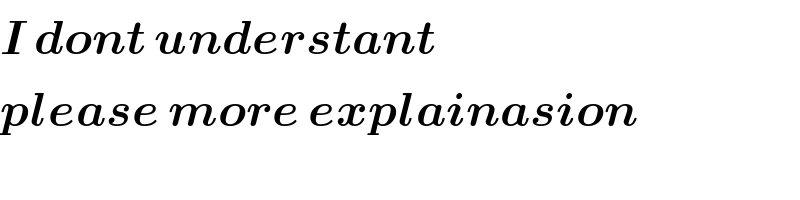
$$\boldsymbol{{I}}\:\boldsymbol{{dont}}\:\boldsymbol{{understant}} \\ $$$$\boldsymbol{{please}}\:\boldsymbol{{more}}\:\boldsymbol{{explainasion}} \\ $$
Commented by rahul 19 last updated on 22/Mar/19

$$\:\mathrm{6}\:\underset{\underset{\mathrm{4}{ways}} {\downarrow}} {−}\:\underset{\underset{\mathrm{3}{ways}} {\downarrow}} {−}\:\underset{\underset{\mathrm{2}{ways}} {\downarrow}} {−}\:\underset{\underset{\:^{\mathrm{3}} {C}_{\mathrm{1}} } {\downarrow}} {−} \\ $$$${similarly}\:{for}\:{digits}\:{starting}\:{with}\:\:\mathrm{8}. \\ $$$$\mathrm{7}\:\underset{\underset{\mathrm{4}{ways}} {\downarrow}} {−}\:\underset{\underset{\mathrm{3}{ways}} {\downarrow}} {−}\:\underset{\underset{\mathrm{2}{ways}} {\downarrow}} {−}\:\underset{\underset{\:^{\mathrm{2}} {C}_{\mathrm{1}} ^{} } {\downarrow}} {−} \\ $$$$\:{Similarly}\:{for}\:{digits}\:{starting}\:{with}\:\mathrm{9}.\:\:\:\:\: \\ $$$$\Rightarrow\:\mathrm{2}\left(\mathrm{4}×\mathrm{3}×\mathrm{2}×\mathrm{3}\right)+\mathrm{2}\left(\mathrm{4}×\mathrm{3}×\mathrm{2}×\mathrm{2}\right)=\mathrm{240}. \\ $$$$\left({Dear}\:{pieroo},\right. \\ $$$${in}\:{this}\:{sol}^{{n}\:} \:{i}'{ve}\:{counted}\:\mathrm{5}−{digit}\:{no}.{s} \\ $$$$\left.{only}!\:{So}\:{this}\:{sol}^{{n}} \:{is}\:{incomplete}.\right) \\ $$
Commented by mr W last updated on 22/Mar/19

$${this}\:{is}\:{correct}\:{for}\:\mathrm{5}−{digit}\:{numbers}. \\ $$$${but}\:{you}\:{can}\:{also}\:{make}\:\mathrm{6}−{digit}\:{numbers}. \\ $$$${they}\:{are}\:{all}\:{greater}\:{than}\:\mathrm{60000}. \\ $$
Commented by mr W last updated on 22/Mar/19
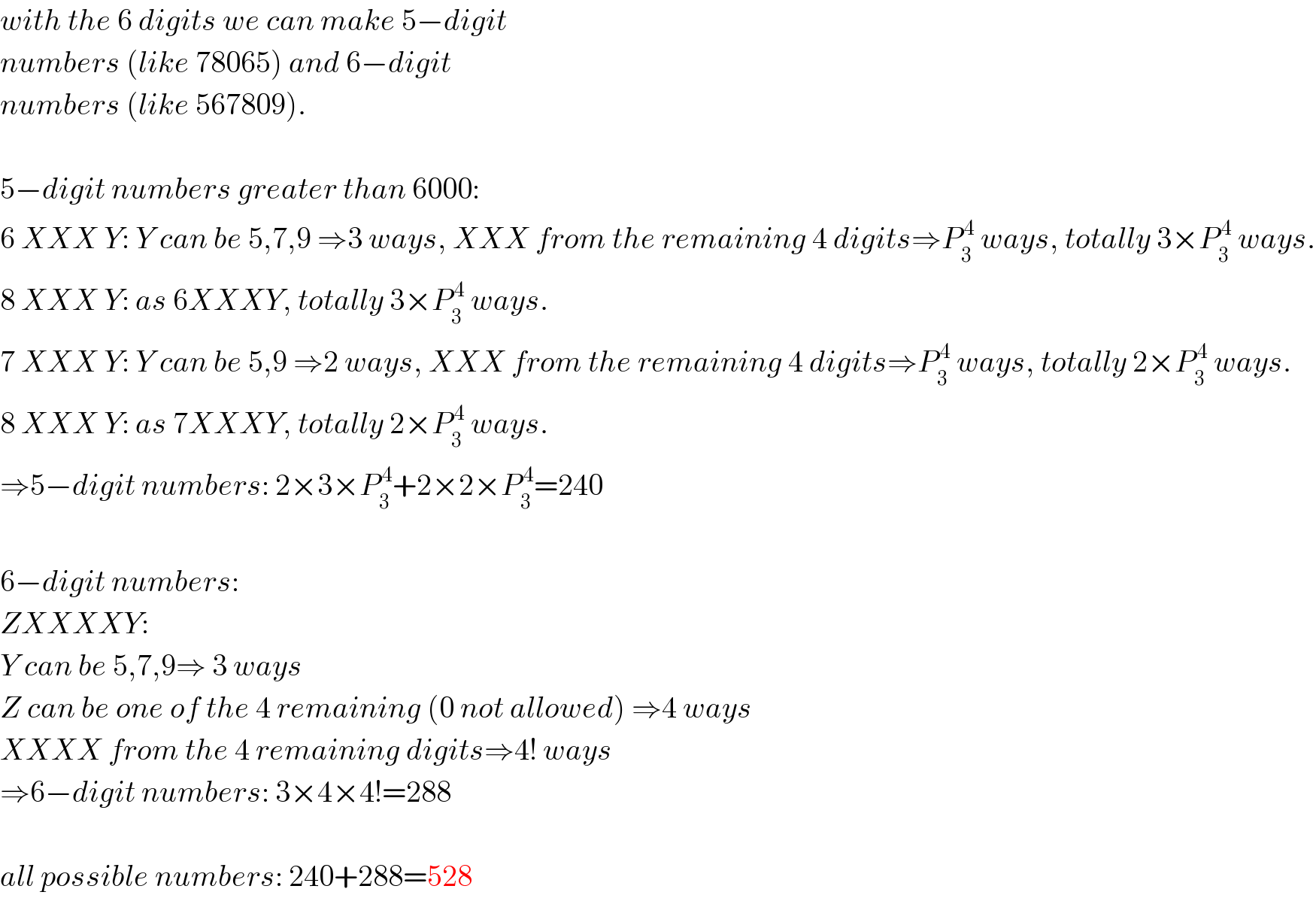
$${with}\:{the}\:\mathrm{6}\:{digits}\:{we}\:{can}\:{make}\:\mathrm{5}−{digit} \\ $$$${numbers}\:\left({like}\:\mathrm{78065}\right)\:{and}\:\mathrm{6}−{digit} \\ $$$${numbers}\:\left({like}\:\mathrm{567809}\right). \\ $$$$ \\ $$$$\mathrm{5}−{digit}\:{numbers}\:{greater}\:{than}\:\mathrm{6000}: \\ $$$$\mathrm{6}\:{XXX}\:{Y}:\:{Y}\:{can}\:{be}\:\mathrm{5},\mathrm{7},\mathrm{9}\:\Rightarrow\mathrm{3}\:{ways},\:{XXX}\:{from}\:{the}\:{remaining}\:\mathrm{4}\:{digits}\Rightarrow{P}_{\mathrm{3}} ^{\:\mathrm{4}} \:{ways},\:{totally}\:\mathrm{3}×{P}_{\mathrm{3}} ^{\:\mathrm{4}} \:{ways}. \\ $$$$\mathrm{8}\:{XXX}\:{Y}:\:{as}\:\mathrm{6}{XXXY},\:{totally}\:\mathrm{3}×{P}_{\mathrm{3}} ^{\:\mathrm{4}} \:{ways}. \\ $$$$\mathrm{7}\:{XXX}\:{Y}:\:{Y}\:{can}\:{be}\:\mathrm{5},\mathrm{9}\:\Rightarrow\mathrm{2}\:{ways},\:{XXX}\:{from}\:{the}\:{remaining}\:\mathrm{4}\:{digits}\Rightarrow{P}_{\mathrm{3}} ^{\:\mathrm{4}} \:{ways},\:{totally}\:\mathrm{2}×{P}_{\mathrm{3}} ^{\:\mathrm{4}} \:{ways}. \\ $$$$\mathrm{8}\:{XXX}\:{Y}:\:{as}\:\mathrm{7}{XXXY},\:{totally}\:\mathrm{2}×{P}_{\mathrm{3}} ^{\:\mathrm{4}} \:{ways}. \\ $$$$\Rightarrow\mathrm{5}−{digit}\:{numbers}:\:\mathrm{2}×\mathrm{3}×{P}_{\mathrm{3}} ^{\:\mathrm{4}} +\mathrm{2}×\mathrm{2}×{P}_{\mathrm{3}} ^{\:\mathrm{4}} =\mathrm{240} \\ $$$$ \\ $$$$\mathrm{6}−{digit}\:{numbers}: \\ $$$${ZXXXXY}: \\ $$$${Y}\:{can}\:{be}\:\mathrm{5},\mathrm{7},\mathrm{9}\Rightarrow\:\mathrm{3}\:{ways} \\ $$$${Z}\:{can}\:{be}\:{one}\:{of}\:{the}\:\mathrm{4}\:{remaining}\:\left(\mathrm{0}\:{not}\:{allowed}\right)\:\Rightarrow\mathrm{4}\:{ways} \\ $$$${XXXX}\:{from}\:{the}\:\mathrm{4}\:{remaining}\:{digits}\Rightarrow\mathrm{4}!\:{ways} \\ $$$$\Rightarrow\mathrm{6}−{digit}\:{numbers}:\:\mathrm{3}×\mathrm{4}×\mathrm{4}!=\mathrm{288} \\ $$$$ \\ $$$${all}\:{possible}\:{numbers}:\:\mathrm{240}+\mathrm{288}=\mathrm{528} \\ $$
Commented by rahul 19 last updated on 22/Mar/19

$$\left.{Thank}\:{You}\:{Sir}!\::\right) \\ $$
Commented by malwaan last updated on 28/Mar/19
$${thank}\:{you}\:{so}\:{much}\:{sir} \\ $$
