Question Number 57051 by Hassen_Timol last updated on 29/Mar/19
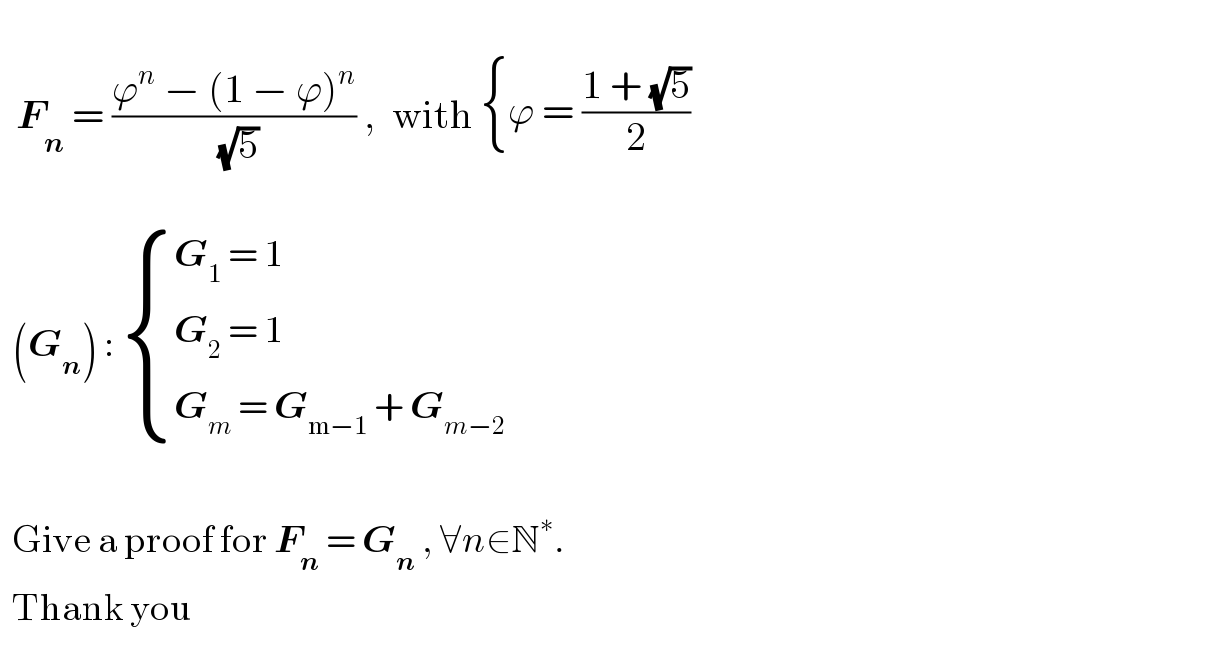
$$ \\ $$$$\:\:\boldsymbol{{F}}_{\boldsymbol{{n}}} \:=\:\frac{\varphi^{{n}} \:−\:\left(\mathrm{1}\:−\:\varphi\right)^{{n}} }{\:\sqrt{\mathrm{5}}}\:,\:\:\mathrm{with}\:\begin{cases}{\varphi\:=\:\frac{\mathrm{1}\:+\:\sqrt{\mathrm{5}}}{\mathrm{2}}}\end{cases} \\ $$$$ \\ $$$$\:\:\left(\boldsymbol{{G}}_{\boldsymbol{{n}}} \right)\::\:\begin{cases}{\boldsymbol{{G}}_{\mathrm{1}} \:=\:\mathrm{1}}\\{\boldsymbol{{G}}_{\mathrm{2}} \:=\:\mathrm{1}}\\{\boldsymbol{{G}}_{{m}} \:=\:\boldsymbol{{G}}_{\mathrm{m}−\mathrm{1}} \:+\:\boldsymbol{{G}}_{{m}−\mathrm{2}} }\end{cases} \\ $$$$ \\ $$$$\:\:\mathrm{Give}\:\mathrm{a}\:\mathrm{proof}\:\mathrm{for}\:\boldsymbol{{F}}_{\boldsymbol{{n}}} \:=\:\boldsymbol{{G}}_{\boldsymbol{{n}}} \:,\:\forall{n}\in\mathbb{N}^{\ast} .\: \\ $$$$\:\:\mathrm{Thank}\:\mathrm{you} \\ $$
Commented by prakash jain last updated on 29/Mar/19
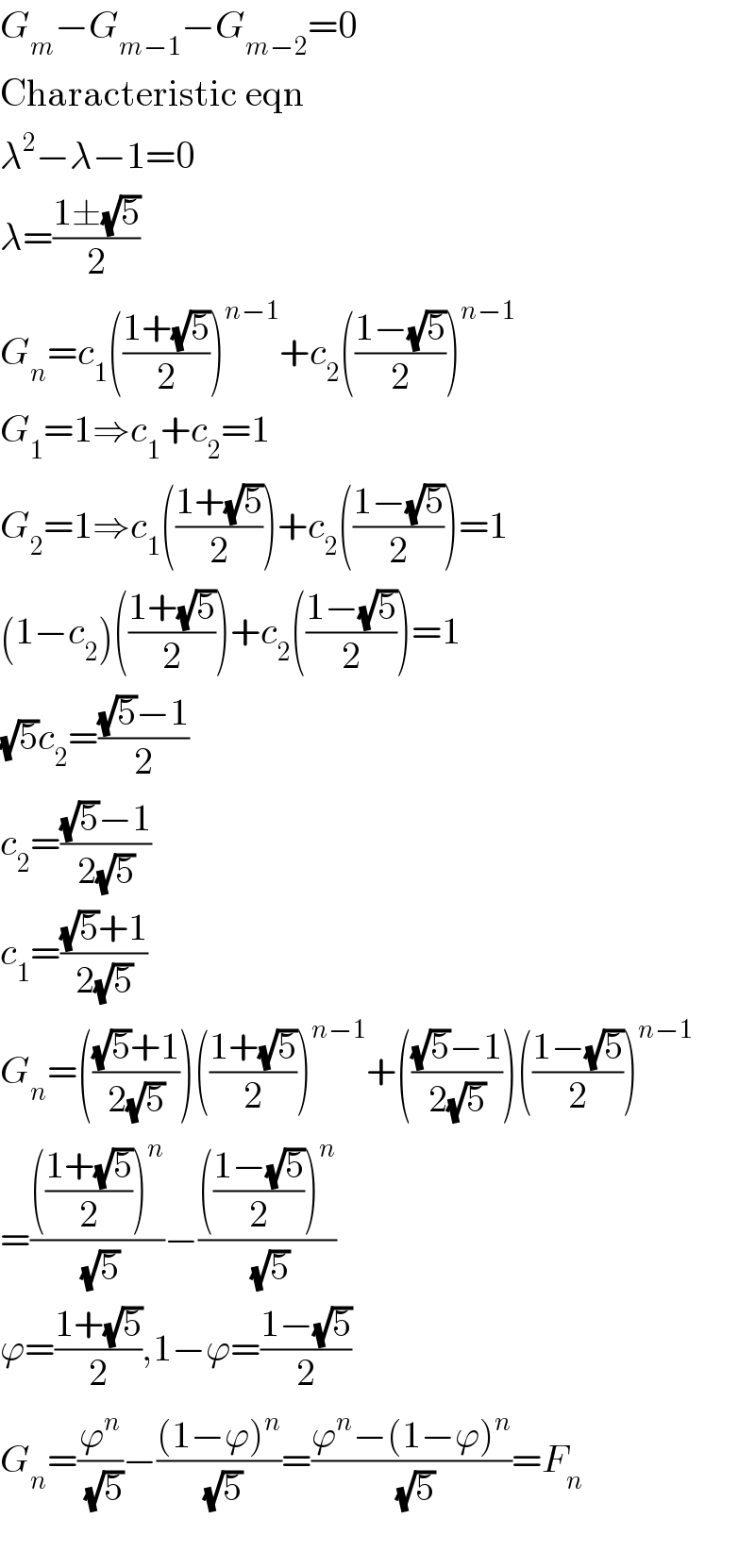
$${G}_{{m}} −{G}_{{m}−\mathrm{1}} −{G}_{{m}−\mathrm{2}} =\mathrm{0} \\ $$$$\mathrm{Characteristic}\:\mathrm{eqn} \\ $$$$\lambda^{\mathrm{2}} −\lambda−\mathrm{1}=\mathrm{0} \\ $$$$\lambda=\frac{\mathrm{1}\pm\sqrt{\mathrm{5}}}{\mathrm{2}} \\ $$$${G}_{{n}} ={c}_{\mathrm{1}} \left(\frac{\mathrm{1}+\sqrt{\mathrm{5}}}{\mathrm{2}}\right)^{{n}−\mathrm{1}} +{c}_{\mathrm{2}} \left(\frac{\mathrm{1}−\sqrt{\mathrm{5}}}{\mathrm{2}}\right)^{{n}−\mathrm{1}} \\ $$$${G}_{\mathrm{1}} =\mathrm{1}\Rightarrow{c}_{\mathrm{1}} +{c}_{\mathrm{2}} =\mathrm{1} \\ $$$${G}_{\mathrm{2}} =\mathrm{1}\Rightarrow{c}_{\mathrm{1}} \left(\frac{\mathrm{1}+\sqrt{\mathrm{5}}}{\mathrm{2}}\right)+{c}_{\mathrm{2}} \left(\frac{\mathrm{1}−\sqrt{\mathrm{5}}}{\mathrm{2}}\right)=\mathrm{1} \\ $$$$\left(\mathrm{1}−{c}_{\mathrm{2}} \right)\left(\frac{\mathrm{1}+\sqrt{\mathrm{5}}}{\mathrm{2}}\right)+{c}_{\mathrm{2}} \left(\frac{\mathrm{1}−\sqrt{\mathrm{5}}}{\mathrm{2}}\right)=\mathrm{1} \\ $$$$\sqrt{\mathrm{5}}{c}_{\mathrm{2}} =\frac{\sqrt{\mathrm{5}}−\mathrm{1}}{\mathrm{2}} \\ $$$${c}_{\mathrm{2}} =\frac{\sqrt{\mathrm{5}}−\mathrm{1}}{\mathrm{2}\sqrt{\mathrm{5}}} \\ $$$${c}_{\mathrm{1}} =\frac{\sqrt{\mathrm{5}}+\mathrm{1}}{\mathrm{2}\sqrt{\mathrm{5}}} \\ $$$${G}_{{n}} =\left(\frac{\sqrt{\mathrm{5}}+\mathrm{1}}{\mathrm{2}\sqrt{\mathrm{5}}}\right)\left(\frac{\mathrm{1}+\sqrt{\mathrm{5}}}{\mathrm{2}}\right)^{{n}−\mathrm{1}} +\left(\frac{\sqrt{\mathrm{5}}−\mathrm{1}}{\mathrm{2}\sqrt{\mathrm{5}}}\right)\left(\frac{\mathrm{1}−\sqrt{\mathrm{5}}}{\mathrm{2}}\right)^{{n}−\mathrm{1}} \\ $$$$=\frac{\left(\frac{\mathrm{1}+\sqrt{\mathrm{5}}}{\mathrm{2}}\right)^{{n}} }{\:\sqrt{\mathrm{5}}}−\frac{\left(\frac{\mathrm{1}−\sqrt{\mathrm{5}}}{\mathrm{2}}\right)^{{n}} }{\:\sqrt{\mathrm{5}}} \\ $$$$\varphi=\frac{\mathrm{1}+\sqrt{\mathrm{5}}}{\mathrm{2}},\mathrm{1}−\varphi=\frac{\mathrm{1}−\sqrt{\mathrm{5}}}{\mathrm{2}} \\ $$$${G}_{{n}} =\frac{\varphi^{{n}} }{\:\sqrt{\mathrm{5}}}−\frac{\left(\mathrm{1}−\varphi\right)^{{n}} }{\:\sqrt{\mathrm{5}}}=\frac{\varphi^{{n}} −\left(\mathrm{1}−\varphi\right)^{{n}} }{\:\sqrt{\mathrm{5}}}={F}_{{n}} \\ $$$$ \\ $$
Commented by Hassen_Timol last updated on 29/Mar/19
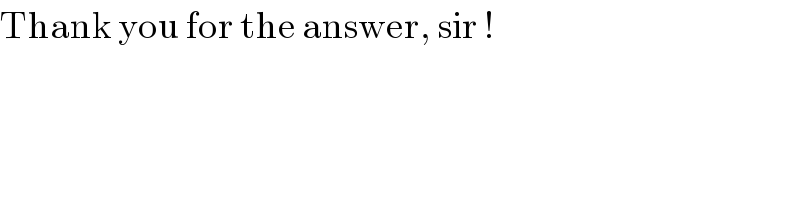
$$\mathrm{Thank}\:\mathrm{you}\:\mathrm{for}\:\mathrm{the}\:\mathrm{answer},\:\mathrm{sir}\:! \\ $$
Commented by Hassen_Timol last updated on 29/Mar/19

$$\mathrm{Could}\:\mathrm{you}\:\mathrm{explain},\:\mathrm{please},\:\mathrm{a}\:\mathrm{little}\:\mathrm{bit} \\ $$$$\mathrm{more}\:\mathrm{in}\:\mathrm{details}\:?\:\mathrm{it}\:\mathrm{would}\:\mathrm{be}\:\mathrm{helpful}… \\ $$
Commented by mr W last updated on 29/Mar/19

$${see}\:{Q}\mathrm{56864},\:{maybe}\:{it}\:{can}\:{help}\:{you}\:{to} \\ $$$${understand}\:{how}\:{to}\:{find}\:{explict}\:{formula} \\ $$$${for}\:{G}_{{m}} . \\ $$
Commented by Hassen_Timol last updated on 30/Mar/19

$$\mathrm{Thank}\:\mathrm{you} \\ $$
