Question Number 122605 by bramlexs22 last updated on 18/Nov/20

Answered by Dwaipayan Shikari last updated on 18/Nov/20
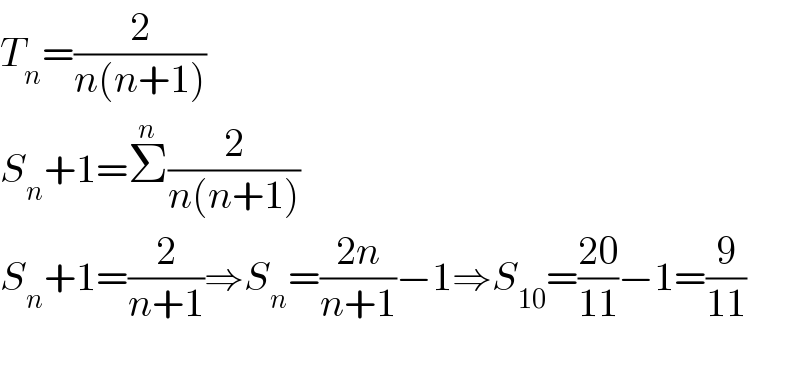
$${T}_{{n}} =\frac{\mathrm{2}}{{n}\left({n}+\mathrm{1}\right)} \\ $$$${S}_{{n}} +\mathrm{1}=\overset{{n}} {\sum}\frac{\mathrm{2}}{{n}\left({n}+\mathrm{1}\right)} \\ $$$${S}_{{n}} +\mathrm{1}=\frac{\mathrm{2}}{{n}+\mathrm{1}}\Rightarrow{S}_{{n}} =\frac{\mathrm{2}{n}}{{n}+\mathrm{1}}−\mathrm{1}\Rightarrow{S}_{\mathrm{10}} =\frac{\mathrm{20}}{\mathrm{11}}−\mathrm{1}=\frac{\mathrm{9}}{\mathrm{11}} \\ $$$$ \\ $$
Answered by MJS_new last updated on 18/Nov/20
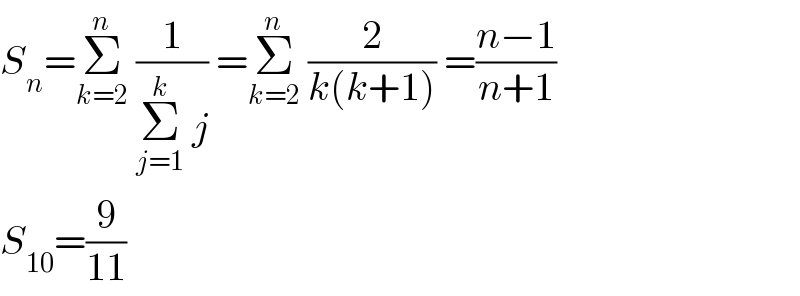
$${S}_{{n}} =\underset{{k}=\mathrm{2}} {\overset{{n}} {\sum}}\:\frac{\mathrm{1}}{\underset{{j}=\mathrm{1}} {\overset{{k}} {\sum}}\:{j}}\:=\underset{{k}=\mathrm{2}} {\overset{{n}} {\sum}}\:\frac{\mathrm{2}}{{k}\left({k}+\mathrm{1}\right)}\:=\frac{{n}−\mathrm{1}}{{n}+\mathrm{1}} \\ $$$${S}_{\mathrm{10}} =\frac{\mathrm{9}}{\mathrm{11}} \\ $$
Commented by bramlexs22 last updated on 18/Nov/20
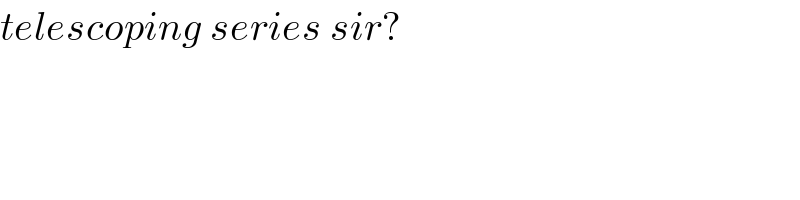
$${telescoping}\:{series}\:{sir}? \\ $$
